A copper disc of radius 0.1 m is roated about its centre with 20 revolutions per second in a uniform magnetic field of 0.1 T with its plane perpendicular the field. The emf induced across the radius of disc is
π20 volt
π10 volt
20π millivolt
100π millivolt
The correct Answer is:C
To find the induced EMF across the radius of a rotating copper disc in a magnetic field, we can follow these steps:
Step 1: Identify the given values
- Radius of the disc, R=0.1m
- Revolutions per second, f=20rev/s
- Magnetic field strength, B=0.1T
Step 2: Convert revolutions per second to angular velocity
The angular velocity ω in radians per second can be calculated using the formula:
ω=2πf
Substituting the value of f:
ω=2π×20=40πrad/s
Step 3: Set up the formula for induced EMF
The induced EMF (ε) across the radius of the disc can be calculated using the formula:
ε=12BωR2
Where:
- B is the magnetic field,
- ω is the angular velocity,
- R is the radius of the disc.
Step 4: Substitute the values into the formula
Now we substitute the values we have:
ε=12×0.1T×40πrad/s×(0.1m)2
Calculating (0.1m)2:
(0.1)2=0.01m2
Now substituting this back into the equation:
ε=12×0.1×40π×0.01
Step 5: Calculate the induced EMF
Calculating the values step-by-step:
ε=12×0.1×40π×0.01=0.0005×40π
ε=0.02πV
Now, calculating 0.02π:
ε≈0.0628V
Converting to millivolts:
ε≈62.8mV
Final Answer
The induced EMF across the radius of the disc is approximately 62.8 mV.
---
- Radius of the disc, R=0.1m
- Revolutions per second, f=20rev/s
- Magnetic field strength, B=0.1T
The angular velocity ω in radians per second can be calculated using the formula:
ω=2πf
Substituting the value of f:
ω=2π×20=40πrad/s
The induced EMF (ε) across the radius of the disc can be calculated using the formula:
ε=12BωR2
Where:
- B is the magnetic field,
- ω is the angular velocity,
- R is the radius of the disc.
Now we substitute the values we have:
ε=12×0.1T×40πrad/s×(0.1m)2
Calculating (0.1m)2:
(0.1)2=0.01m2
Now substituting this back into the equation:
ε=12×0.1×40π×0.01
Calculating the values step-by-step:
ε=12×0.1×40π×0.01=0.0005×40π
ε=0.02πV
Now, calculating 0.02π:
ε≈0.0628V
Converting to millivolts:
ε≈62.8mV
The induced EMF across the radius of the disc is approximately 62.8 mV.
Similar Questions
A copper disc of radius 0.1 m is rotated about its natural axis with 10 rps in a uniform magnetic field of 0.1 T with its plane perpendicular to the field, The emf induced across the radius of the disc is
View SolutionA copper disc of radius 1 m is rotated about its natural axis with an angular velocity 2 rad/sec in a uniform magnetic field of 5 tesla with its plane perpendicular to the field. Find the emf induced between the centre of the disc and its rim.
View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
A coil is rotated in a uniform magnetic field about an axis perpendicular to the field. The emf induced in the coil would be maximum when the plane of coil is :
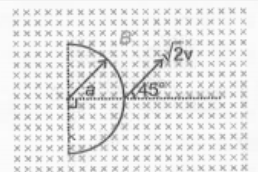
View SolutionA semicircular conducting wire of radius a is moving perpendicular to a uniform magnetic field B with speed√2vas shown in the figure.The emf induced across the wire Is
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/ s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
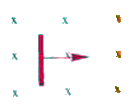
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
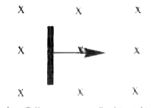
View SolutionA circular copper disc 100cm in radius rotates at 20πrad/s about an axis through its centre and perpendicular to the disc. A uniform magnetic field of 0.2T acts perpendicular to the disc. Calculate the potential difference developed between the axis of the disc and the rim
View SolutionA straight conductor 0.1 m long moves in a uniform magnetic field 0.1 T. The velocity of the conductor is 15ms−1 and is directed perpendicular to the field. The emf induced between the two ends of the conductor is
View SolutionA conducting rod is rotated about one end in a plane perpendicular to a uniform magnetic field with constant angular velocity. The correct graph between the induced emf (e) across the rod and time (t) is
View Solution
