A conducting rod is rotated about one end in a plane perpendicular to a uniform magnetic field with constant angular velocity. The correct graph between the induced emf (e) across the rod and time (t) is


The correct Answer is:C
To solve the problem, we need to analyze the situation step by step.
1. Understanding the Setup:
- We have a conducting rod that is rotated about one end in a plane perpendicular to a uniform magnetic field.
- The magnetic field is uniform and directed into the plane (indicated by a cross sign).
2. Identifying the Motion:
- As the rod rotates, it sweeps out an area in the magnetic field. The angular velocity of the rod is constant, denoted as ω.
3. Calculating the Induced EMF:
- The induced EMF (e) in the rod can be calculated using Faraday's law of electromagnetic induction, which states that:
e=−dΦdt
- Here, Φ is the magnetic flux through the area swept by the rod.
4. Finding the Magnetic Flux:
- The magnetic flux Φ is given by:
Φ=B⋅A
- Where B is the magnetic field strength, and A is the area swept by the rod.
5. Calculating the Area Swept:
- As the rod rotates, the area A swept out in a small time dt can be expressed as:
dA=12L2dθ
- Where L is the length of the rod and dθ is the small angle swept in time dt.
6. Substituting into the Flux Equation:
- The magnetic flux can now be expressed as:
Φ=B⋅12L2θ
- Taking the derivative with respect to time t:
dΦdt=B⋅12L2dθdt
7. Using the Constant Angular Velocity:
- Since dθdt=ω (constant angular velocity), we have:
dΦdt=B⋅12L2ω
8. Calculating the Induced EMF:
- Substituting back into the EMF equation:
e=−dΦdt=−B⋅12L2ω
- Since B, L, and ω are constants, the induced EMF e is also constant.
9. Graphing the Induced EMF vs. Time:
- Since the induced EMF e is constant over time, the graph of e versus t will be a horizontal line.
Conclusion:
The correct graph between the induced EMF (e) across the rod and time (t) is a horizontal line, indicating that e is constant over time.
- We have a conducting rod that is rotated about one end in a plane perpendicular to a uniform magnetic field.
- The magnetic field is uniform and directed into the plane (indicated by a cross sign).
- As the rod rotates, it sweeps out an area in the magnetic field. The angular velocity of the rod is constant, denoted as ω.
- The induced EMF (e) in the rod can be calculated using Faraday's law of electromagnetic induction, which states that:
e=−dΦdt
- Here, Φ is the magnetic flux through the area swept by the rod.
- The magnetic flux Φ is given by:
Φ=B⋅A
- Where B is the magnetic field strength, and A is the area swept by the rod.
- As the rod rotates, the area A swept out in a small time dt can be expressed as:
dA=12L2dθ
- Where L is the length of the rod and dθ is the small angle swept in time dt.
- The magnetic flux can now be expressed as:
Φ=B⋅12L2θ
- Taking the derivative with respect to time t:
dΦdt=B⋅12L2dθdt
- Since dθdt=ω (constant angular velocity), we have:
dΦdt=B⋅12L2ω
- Substituting back into the EMF equation:
e=−dΦdt=−B⋅12L2ω
- Since B, L, and ω are constants, the induced EMF e is also constant.
- Since the induced EMF e is constant over time, the graph of e versus t will be a horizontal line.
The correct graph between the induced EMF (e) across the rod and time (t) is a horizontal line, indicating that e is constant over time.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective Questions
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Subjective
21 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
View SolutionA copper rod of length l is rotated about one end perpendicular to the magnetic field B with constant angular velocity ω . The induced e.m.f between the two ends is
View Solution
Knowledge Check
A uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity omega in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
Amω2L2AYBmω2L22AYCmω2L23AYD2mω2L2AY
A conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
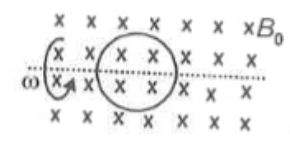
View SolutionA circular loop of radius 'a' is rotated in a uniform magnetic field B, with constant angular velocity o about diameter as shown in the figure. Choose the correct graph of induced emf & versus time t. (consider at t = 0 area vector of loop is in the direction of magnetic field)
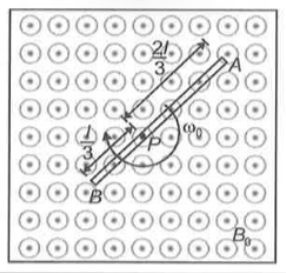
View SolutionA conducting rod of length / is rotating about point Pin a uniform transverse magnetic field B0 as shown in the figure. If angular speed of the rod is ω0 then the magnitude of induced emf across the ends of the rod will be (PA=2l3andPB=l3)
View SolutionA metal rod of length 2 m is rotating with an angualr velocity of 100rads−1 in plane perpendicular to a uniform magnetic field of 0.3 T. The potential difference between the ends of the rod is
View SolutionAssertion A conducting loop is rotated in a uniform magnetic field with constant angular velocity ω as shown in figure. At time t = 0, plane of the loop is perpendicular to the magnetic field. Induced emf produced in the loop is maximum when plane of loop is parallel to magnetic field.
Reason When plane of loop is parallel to magnetic field, then magnetic flux passing through the loop is zero.
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA copper disc of radius 0.1 m is rotated about its natural axis with 10 rps in a uniform magnetic field of 0.1 T with its plane perpendicular to the field, The emf induced across the radius of the disc is
View Solution
