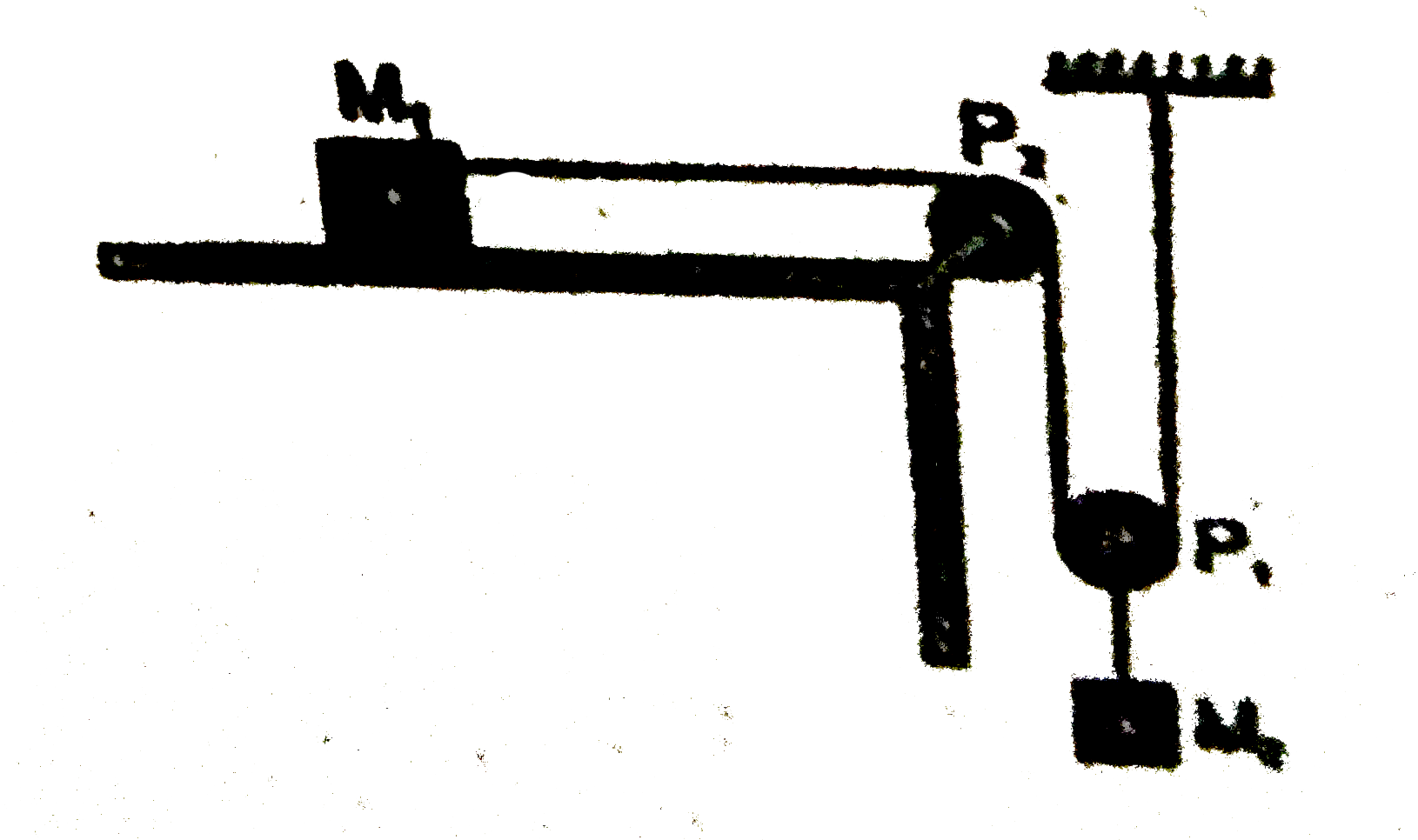
Masses M1,M2 and M3 are connected by strings of negligible mass which pass over massless and frictionless pulleys P1 and P2 as shown in the figure. The masses move such that the portion of the string betweenP1 and P2 is parallel to the inclined plane and the portion of the string between P2 and M3 is horizontal. The masses M2 and M3 are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass M1 moves downwards with a uniform velocity, find
(i) the mass of M1 in kg
(ii) the tension in the horizontal portion of the string in Newton
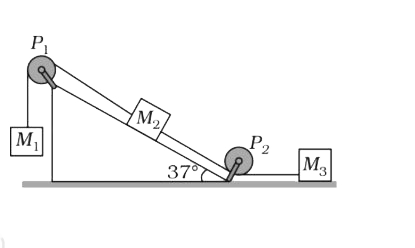
The correct Answer is:5
Step by step video & image solution for Masses M_(1), M_(2) and M_(3) are connected by strings of negligible mass which pass over massless and frictionless pulleys P_(1) and P_(2) as shown in the figure. The masses move such that the portion of the string betweenP_(1) and P_(2) is parallel to the inclined plane and the portion of the string between P_(2) and M_(3) is horizontal. The masses M_(2) and M_(3) are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass M_(1) moves downwards with a uniform velocity, find (i) the mass of M_(1) in kg (ii) the tension in the horizontal portion of the string in Newton by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
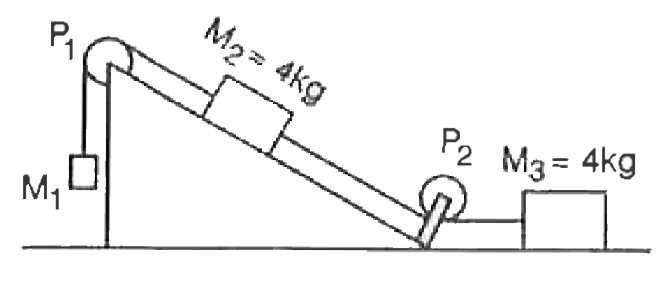
Masses M1,M2andM3 are connected by string of negligible mass which pass over massless and frictionless pulleys P1andP2 as shown in figure 7.15. The masses move such that the string between P1andP2 is parallel to the incline and the portion of the string between P2andM3 is horizontal. The masses M2andM3 are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of 37∘ with the horizontal. If the mass M1moves downwards with a uniform velocity, find (i) the mass of M1, (ii) the tension in the horizontal portion. (g=9.8ms−2,sin37∘=35)
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
View Solution
Knowledge Check
- Question 1 - Select One
A string of negligible mass going over a clamped pulley of mass m supports a block of M as shown in the figure. the force on the pulley by the clamp is given by:
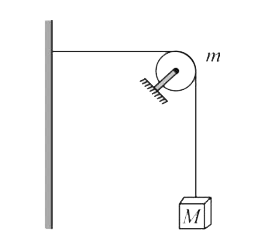A√2MgB√2mgC√(M+m)2+m2gD√(M+m)2+M2g
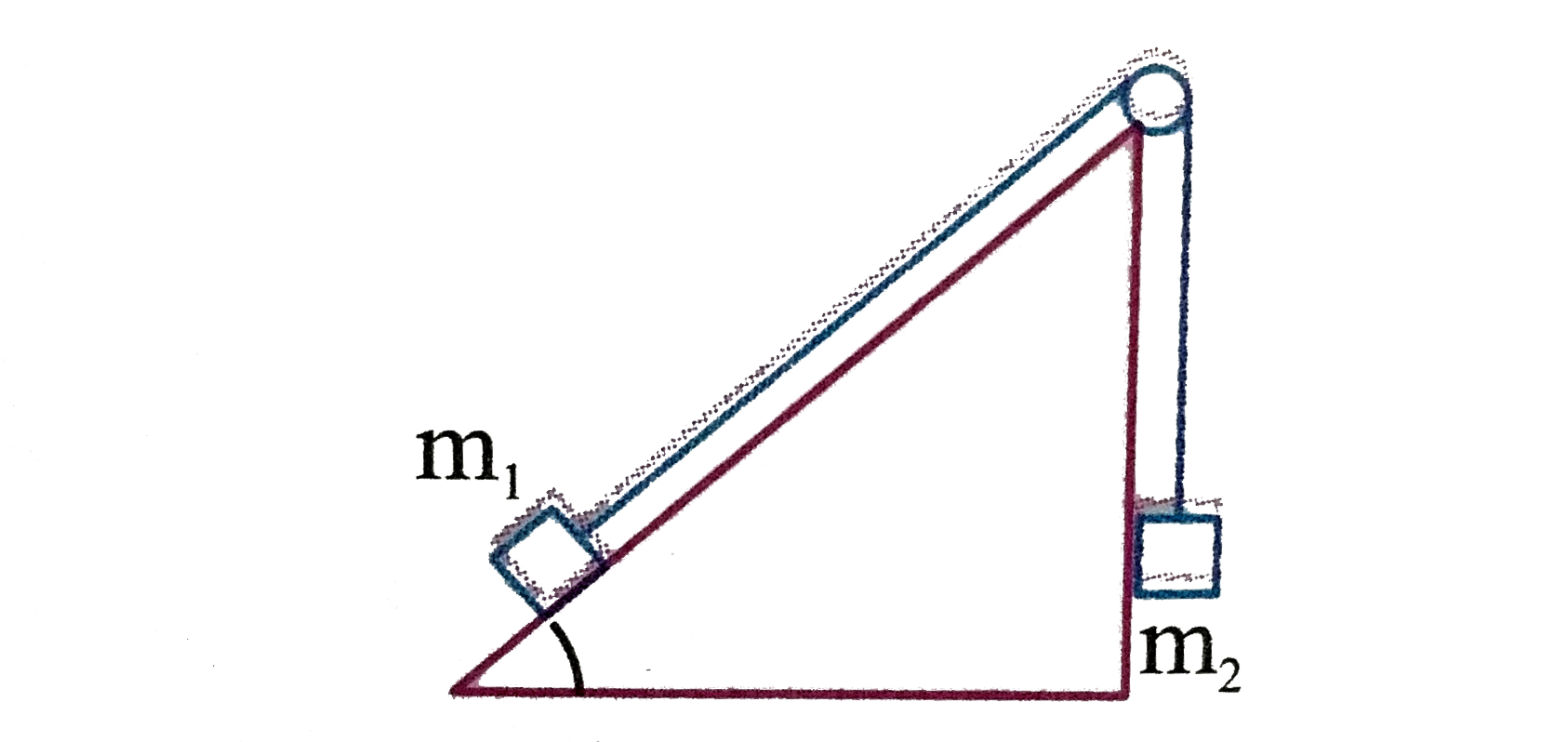
Blocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
View SolutionA string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by
View SolutionThree masses m1=m,m2=2mandm3=3m are hund on a string passing over a frictionless pulley as shown in Figure . The mass of the string in negligible . The system is released from rest.
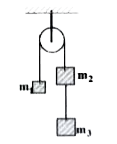
The tension in the string between masses m1andm2 isView SolutionThree masses m1=m,m2=2mandm3=3m are hund on a string passing over a frictionless pulley as shown in Figure . The mass of the string in negligible . The system is released from rest.
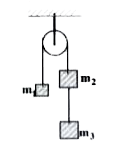
The tension in the string between masses m2andm3 isView SolutionTwo blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
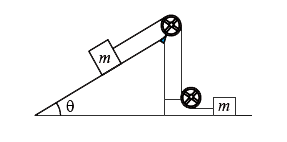
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View SolutionThree equal weights of 3 kg each are hanging on a string passing over a frictionless pulley as shown in figure. The tension in the string between masses II and III will be (Take = 10m/sec2)
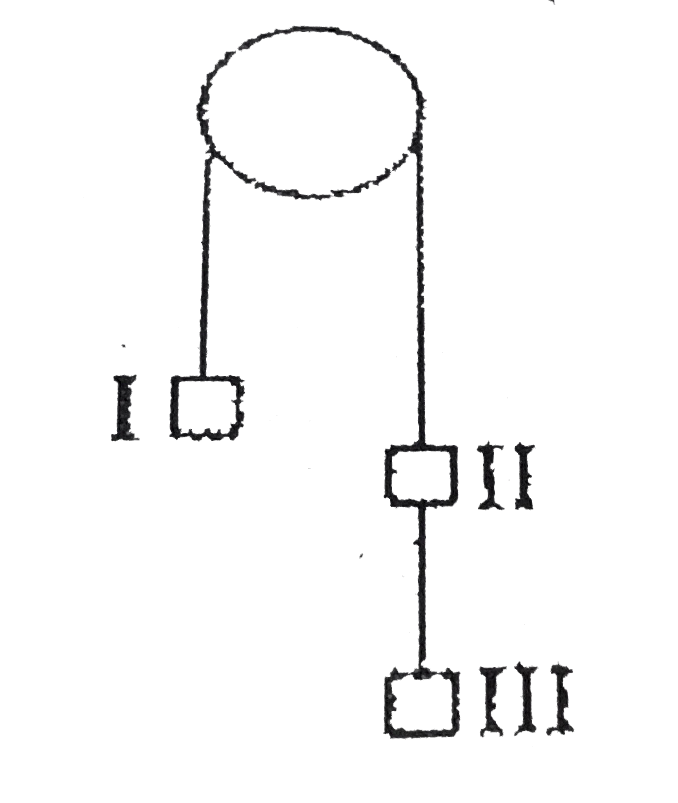
View Solution