it is estimated that per minute, each cm2 of earth recives about 2 calories of heat energy from the sun. This constant is called solar constant S. Express solar constant in SI units.
8kWm−2
1.4kWm−2
1.8kWm−2
2.5kWm_2
To express the solar constant in SI units, we need to convert the given values into appropriate SI units. Let's break down the problem step by step.
Step 1: Understand the given values
The solar constant S is given as:
- 2 calories per square centimeter per minute.
Step 2: Convert calories to joules
We know that:
1 calorie = 4.2 joules
Thus, for 2 calories:
2 calories=2×4.2 joules=8.4 joules
Step 3: Convert area from square centimeters to square meters
We know that:
1 cm = 0.01 m, therefore:
1 cm2=(0.01 m)2=0.0001 m2=10−4 m2
Step 4: Convert time from minutes to seconds
1 minute = 60 seconds.
Step 5: Combine the conversions
Now we can express the solar constant S in SI units:
S=8.4 joules10−4 m2⋅60 seconds
Step 6: Simplify the expression
Calculating the denominator:
10−4 m2⋅60 seconds=60×10−4 m2 seconds
Now substituting this back into the equation:
S=8.460×10−4 joules per meter squared per second
Step 7: Calculate the value
Calculating the numerical value:
S=8.460×104 joules per meter squared per second
S=0.14×104 joules per meter squared per second
S=1.4×103 joules per meter squared per second
Step 8: Convert joules per second to watts
Since 1 watt = 1 joule/second, we can express:
S=1.4×103 watts per meter squared
or
S=1.4 kW/m2
Final Answer
The solar constant S in SI units is:
S=1.4 kW/m2
---
The solar constant S is given as:
- 2 calories per square centimeter per minute.
We know that:
1 calorie = 4.2 joules
2 calories=2×4.2 joules=8.4 joules
We know that:
1 cm = 0.01 m, therefore:
1 cm2=(0.01 m)2=0.0001 m2=10−4 m2
1 minute = 60 seconds.
Now we can express the solar constant S in SI units:
S=8.4 joules10−4 m2⋅60 seconds
Calculating the denominator:
10−4 m2⋅60 seconds=60×10−4 m2 seconds
Now substituting this back into the equation:
S=8.460×10−4 joules per meter squared per second
Calculating the numerical value:
S=8.460×104 joules per meter squared per second
S=0.14×104 joules per meter squared per second
S=1.4×103 joules per meter squared per second
Since 1 watt = 1 joule/second, we can express:
S=1.4×103 watts per meter squared
or
S=1.4 kW/m2
The solar constant S in SI units is:
S=1.4 kW/m2
Similar Questions
A conductor of length L is placed along the x - axis , with one of its ends at x = 0 and the other at x = L. If the rate of flow of heat energy through the conduct is constant and its thermal resistance per unit length is also constant , then Which of the following graphs is/are correct ?
View SolutionSolar constant (S) depends upon the temperature of the Sun
View Solution
Knowledge Check
- Question 1 - Select One
Experimental investigations show that the intensity of solar radiation is maximum for a wavelength 480nm in the visible ragion. Estimate the surface temperature of sun. (Given Wien's constant b=2.88×10−3mK).
A4000KB6000KC8000KD106K
The radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
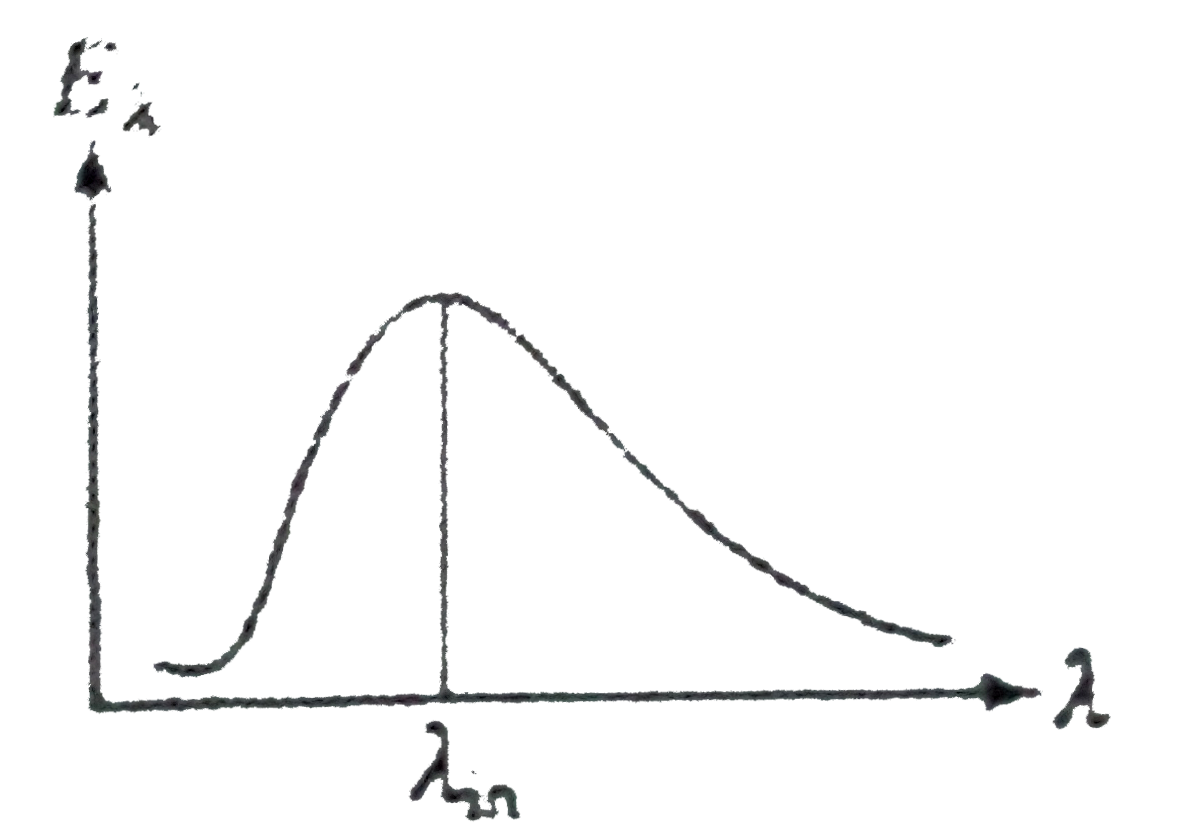
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) isView SolutionSolar constant is defined as energy received by Earth per cm2 per minute. Find the dimensions of solar constant.
View SolutionThe solar constant is the amount of heat energy received per second per unit area of a perfectly black surface placed at a mean distance of the Earth form the Sun, in the absence of Earth's atmosphere, the surface being held perpendicular to the direction of Sun's rays. Its value is 1388W/m2. If the solar constant for the earth is 's'. The surface temperature of the sun is TK,D is the diameter of the sun, R is the mean distance of the Earth from the sun. The sun subtends a small angle 'theta' at the earth. Then correct options is/are:-
View SolutionWould you expect the total energy of the solar system to be constant? What about the total angular momentum? Explain
View SolutionThe radiations emitted by the sun are analyzed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
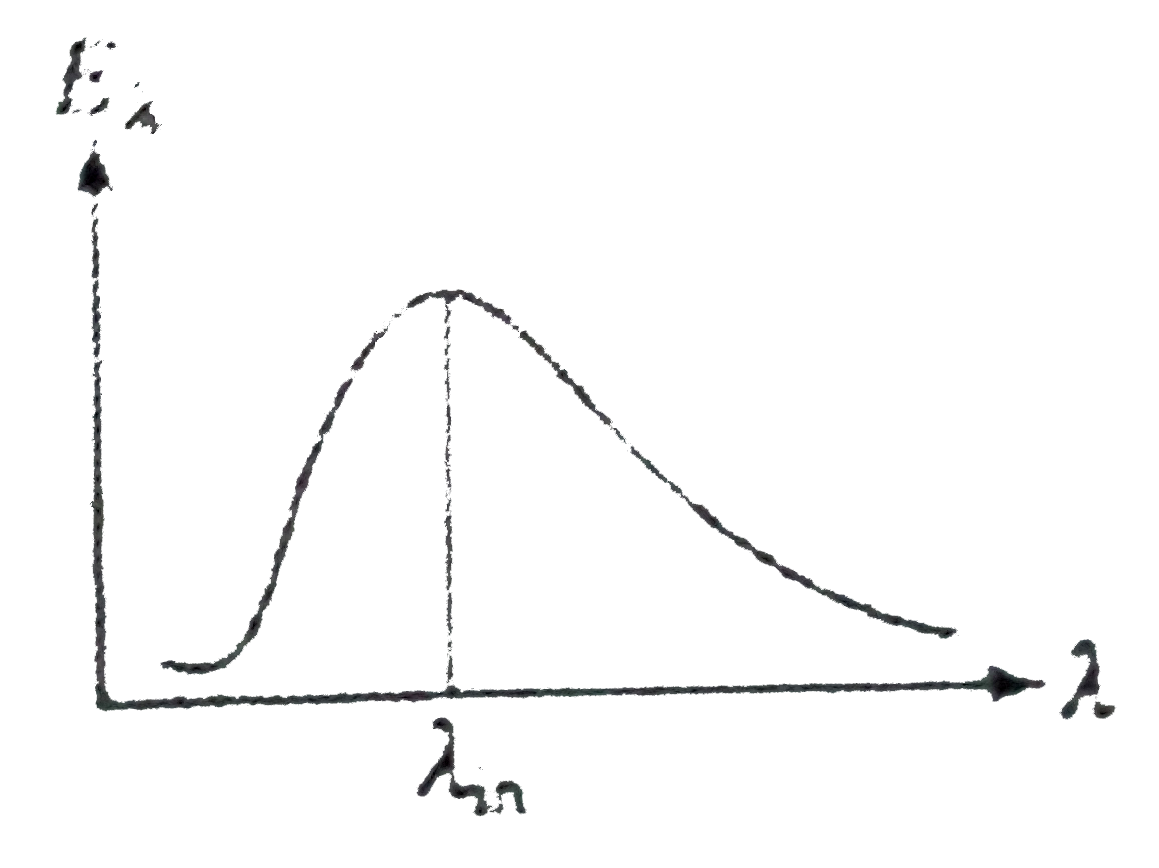
Assume the sun produces energy only by nuclear fusion of hydrogen nuclei and the fraction of nuclear mass of hydrogen that can be converted to energy is η. How long will the sun keep on emittied the energy if the mass of hydrogen at present in Sun's core is m?View SolutionThe solar constant for a planet is S. The surface temperature of the sun is TK. The sun subtends an angle θ at the planet:
View SolutionIf the ratio of specific heat of a gas of constant pressure to that at constant volume is γ, the change in internal energy of the mass of gas, when the volume changes from V to 2V at constant pressure p is
View Solution
