The distance of Neptune and Saturn from the Sun are respectively 1013 and 1012 meters and their periodic times are respectively Tn and Ts. If their orbits are circular, then the value of Tn/Ts is
10
100
10√10
1000
To solve the problem, we need to determine the ratio of the periodic times (T_n/T_s) of Neptune and Saturn based on their distances from the Sun. We can use Kepler's Third Law of Planetary Motion, which states that the square of the period of a planet is directly proportional to the cube of the semi-major axis of its orbit (which we can consider as the radius for circular orbits).
1. Identify the given data:
- Distance of Neptune from the Sun (R_n) = 1013 meters
- Distance of Saturn from the Sun (R_s) = 1012 meters
- Period of Neptune = T_n
- Period of Saturn = T_s
2. Apply Kepler's Third Law:
According to Kepler's Third Law:
T2nT2s=R3nR3s
This implies:
TnTs=(RnRs)3/2
3. Substitute the values of R_n and R_s:
TnTs=(10131012)3/2
4. Simplify the ratio:
TnTs=(1013−12)3/2=(101)3/2=103/2
5. Calculate 103/2:
103/2=101.5=10⋅√10=10√10
6. Final Result:
Thus, the value of TnTs is:
Tn/Ts=10√10
Conclusion:
The final answer is 10√10.
- Distance of Neptune from the Sun (R_n) = 1013 meters
- Distance of Saturn from the Sun (R_s) = 1012 meters
- Period of Neptune = T_n
- Period of Saturn = T_s
According to Kepler's Third Law:
T2nT2s=R3nR3s
This implies:
TnTs=(RnRs)3/2
TnTs=(10131012)3/2
TnTs=(1013−12)3/2=(101)3/2=103/2
103/2=101.5=10⋅√10=10√10
Thus, the value of TnTs is:
Tn/Ts=10√10
The final answer is 10√10.
Similar Questions
The distance of the two planets from the Sun are 1013m and 1012m, respectively. Find the ratio of time periods of the two planets.
View SolutionThe distance of the two planets from the Sun are 1013m and 1012m, respectively. Find the ratio of time periods of the two planets.
View SolutionTwo planets are at distance R1andR2 from the Sun. Their periods are T1andT2 then (T1T2)2 is equal to
View SolutionThe x and y coordinates of the particle at any time are x=5t−2t2andy=10t respectively, where x and y are in meters and t in seconds. The acceleration of the particle at t=2s is:
View SolutionThe x and y coordinates of the particle at any time are x=5t−2t2andy=10t respectively, where x and y are in meters and t in seconds. The acceleration of the particle at t=2s is:
View SolutionThe distance covered by an object (in meter) is given by
s=8t3−7t2+5t
Find its speed at t = 2 s.
View SolutionThe x and y coordinates if the particle at any time are x=5t−2t2 and t = 10t respectively, where x and y are in meters and t in second.The acceleation of the aprticle at t = 2 s is
View SolutionThe switch S is closed in the circuit shown at time t=0 . The current in the resistor at t=0 and t=∞ are respectively .
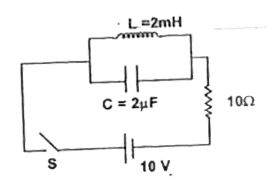
View SolutionTwo satellites A and B of masses m1 and m2(m1=2m2) are moving in circular orbits of radii r1 and r2(r1=4r2), respectively, around the earth. If their periods are TA and TB, then the ratio TA/TB is
View SolutionSuppose a series of n terms given by Sn=t1+t2+t3+. . . .+tn
then Sn−1=t1+t2+t3+. . . .+tn−1,n≥1 subtracting we get Sn−Sn−1=tn,n≥2 surther if we put n=1 is the first sum then S1=t1 thus w can write tn=Sn−Sn−1,n≥2 and t1=S1
Q. The sum of n terms of a series is a.2n−b. where a and b are constant then the series is
View Solution
