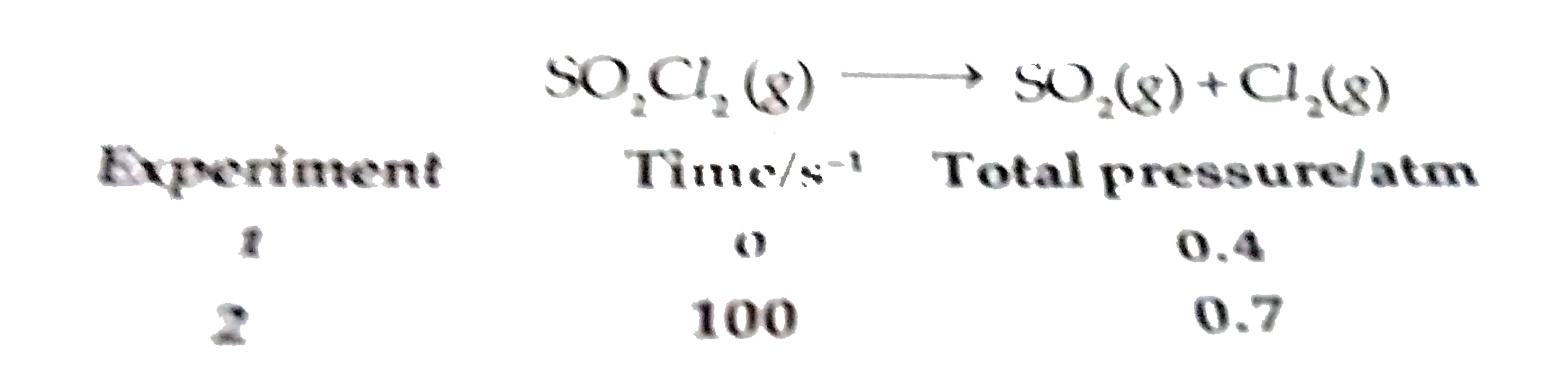The following data is obtained during the first order thermal decomposition of
at constant volume and temperature
The rate constant in is
0.0693
69.3
6.93
To find the rate constant (k) for the first-order thermal decomposition of the reaction 2A(g)→B(g)+C(s), we can follow these steps:
Step 1: Define Initial Conditions
Let the initial pressure of A at time t=0 be P0. Since the reaction produces solid C, it does not contribute to the total pressure.
Step 2: Write the Expression for Total Pressure
At time t, the pressure of A decreases as it decomposes:
- Pressure of A at time t = P0−2P (where P is the change in pressure due to the decomposition of A).
- Pressure of B at time t = P.
- Therefore, the total pressure Ptotal at time t is:
Ptotal=(P0−2P)+P=P0−P
Step 3: Use Given Data to Set Up Equations
From the problem, we have:
1. At the end of 10 minutes, Ptotal=300 mmHg.
2. After completion of the reaction, Ptotal=200 mmHg.
From the completion of the reaction, we know that all of A has decomposed:
P0−2P=200(1)
From the data at 10 minutes:
P0−P=300(2)
Step 4: Solve the Equations
Now, we can solve equations (1) and (2):
1. From equation (2):
P0=300+P
2. Substitute P0 in equation (1):
(300+P)−2P=200
Simplifying gives:
300−P=200⟹P=100
Step 5: Find P0
Substituting P back into the expression for P0:
P0=300+100=400 mmHg
Step 6: Calculate the Rate Constant k
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(P0P0−2P)
Substituting the values:
- t=10 minutes
- P0=400 mmHg
- P0−2P=400−200=200 mmHg
Now, substituting these values into the equation:
k=2.30310log(400200)
k=2.30310log(2)
Using log(2)≈0.3010:
k=2.30310×0.3010=0.0693 min−1
Final Answer
The rate constant k is approximately 0.0693 min−1.
---
Let the initial pressure of A at time t=0 be P0. Since the reaction produces solid C, it does not contribute to the total pressure.
At time t, the pressure of A decreases as it decomposes:
- Pressure of A at time t = P0−2P (where P is the change in pressure due to the decomposition of A).
- Pressure of B at time t = P.
- Therefore, the total pressure Ptotal at time t is:
Ptotal=(P0−2P)+P=P0−P
From the problem, we have:
1. At the end of 10 minutes, Ptotal=300 mmHg.
2. After completion of the reaction, Ptotal=200 mmHg.
P0−2P=200(1)
P0−P=300(2)
Now, we can solve equations (1) and (2):
1. From equation (2):
P0=300+P
2. Substitute P0 in equation (1):
(300+P)−2P=200
Simplifying gives:
300−P=200⟹P=100
Substituting P back into the expression for P0:
P0=300+100=400 mmHg
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(P0P0−2P)
Substituting the values:
- t=10 minutes
- P0=400 mmHg
- P0−2P=400−200=200 mmHg
k=2.30310log(400200)
k=2.30310log(2)
Using log(2)≈0.3010:
k=2.30310×0.3010=0.0693 min−1
The rate constant k is approximately 0.0693 min−1.
Similar Questions
Knowledge Check
The following data were obtained during the first order thermal decomposition of SO2CI2 at a constant volume.
SO2CI2(g)→SO2(g)+CI2(g)
ExperimentTime/s−1Total pressure/atm100.521000.6
What is the rate of reaction when total pressure is 0.65 atm?A0.35atms−1B2.235×10−3atms−1C7.8×10−4atms−1D1.55×10−4atms−1
The following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)

View SolutionThe following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)

View SolutionThe following data were obtained during the first thermal decompoistion of N2O5(g) at constant volume.
2N2O5(g)→2N2O4(g)+O2(g)
∣∣ ∣ ∣∣S.No.Time (s)Total pressure (atm)i.00.5ii.1000.512∣∣ ∣ ∣∣
Calculate the rate constant.
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5 (g) at constant volume :
2N2O5(g)→2N2O4(g)+O2(g)

Calculate the rate constant.
View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at constant volume :
ExperimentTime (s)Total Pressure (atm)100.321000.5
Calculate rate constant
[Given : log 6 = 0.7782, log 3 = 0.4771]
View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume.
SO2Cl2(g)→SO2(g)+Cl2(g)

What is the rate of reaction when total pressure of 0.65 atm?
View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)
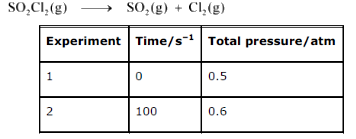
Calculate the rate of the reaction when total pressure is 0.65 atm
View Solution