Find the time after which the particle's initial velocity will be perpendicular to instantaneous velocity whebn it is projected with 30 m/s from horizontal ground by making an angle with vertical
6 second
second
3 second
Never possible
To solve the problem, we need to find the time after which the particle's initial velocity becomes perpendicular to its instantaneous velocity. Let's break down the steps to arrive at the solution.
Step 1: Understand the Initial Conditions
The particle is projected with an initial velocity u=30m/s at an angle of 60∘ with the vertical. This means the angle with the horizontal is 30∘.
Step 2: Resolve the Initial Velocity
We need to resolve the initial velocity into its horizontal and vertical components.
- Horizontal Component (ux):
ux=u⋅sin(30∘)=30⋅12=15m/s
- Vertical Component (uy):
uy=u⋅cos(30∘)=30⋅√32=15√3m/s
Step 3: Determine the Instantaneous Velocity
At any time t, the horizontal component of velocity remains constant (since there is no horizontal acceleration), while the vertical component changes due to gravity.
- Horizontal Component (vx):
vx=ux=15m/s
- Vertical Component (vy):
vy=uy−g⋅t=15√3−10t
Step 4: Find the Condition for Perpendicular Velocities
The initial velocity →u is perpendicular to the instantaneous velocity →v when their dot product is zero:
→u⋅→v=0
This can be expressed as:
ux⋅vx+uy⋅vy=0
Substituting the components:
15⋅15+(15√3)⋅(15√3−10t)=0
Step 5: Simplify the Equation
Expanding the equation:
225+15⋅15⋅3−150√3t=0
225+675−150√3t=0
900=150√3t
Step 6: Solve for Time t
Rearranging gives:
t=900150√3=6√3=2√3seconds
Step 7: Final Answer
Thus, the time after which the particle's initial velocity will be perpendicular to the instantaneous velocity is:
t=2√3seconds≈3.46seconds
The particle is projected with an initial velocity u=30m/s at an angle of 60∘ with the vertical. This means the angle with the horizontal is 30∘.
We need to resolve the initial velocity into its horizontal and vertical components.
ux=u⋅sin(30∘)=30⋅12=15m/s
uy=u⋅cos(30∘)=30⋅√32=15√3m/s
At any time t, the horizontal component of velocity remains constant (since there is no horizontal acceleration), while the vertical component changes due to gravity.
vx=ux=15m/s
vy=uy−g⋅t=15√3−10t
The initial velocity →u is perpendicular to the instantaneous velocity →v when their dot product is zero:
→u⋅→v=0
This can be expressed as:
ux⋅vx+uy⋅vy=0
15⋅15+(15√3)⋅(15√3−10t)=0
Expanding the equation:
225+15⋅15⋅3−150√3t=0
225+675−150√3t=0
900=150√3t
Rearranging gives:
t=900150√3=6√3=2√3seconds
Thus, the time after which the particle's initial velocity will be perpendicular to the instantaneous velocity is:
t=2√3seconds≈3.46seconds
Similar Questions
Two particle are projected with same initial velocities at an angle 30∘ and 60∘ with the horizontal .Then
View SolutionA body is projected with a velocity of 30m/s to have to horizontal range of 45m. Find the angle of projection .
View SolutionA body is projected with an initial Velocity 20 m/s at 60° to the horizontal. Its velocity after 1 sec is
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
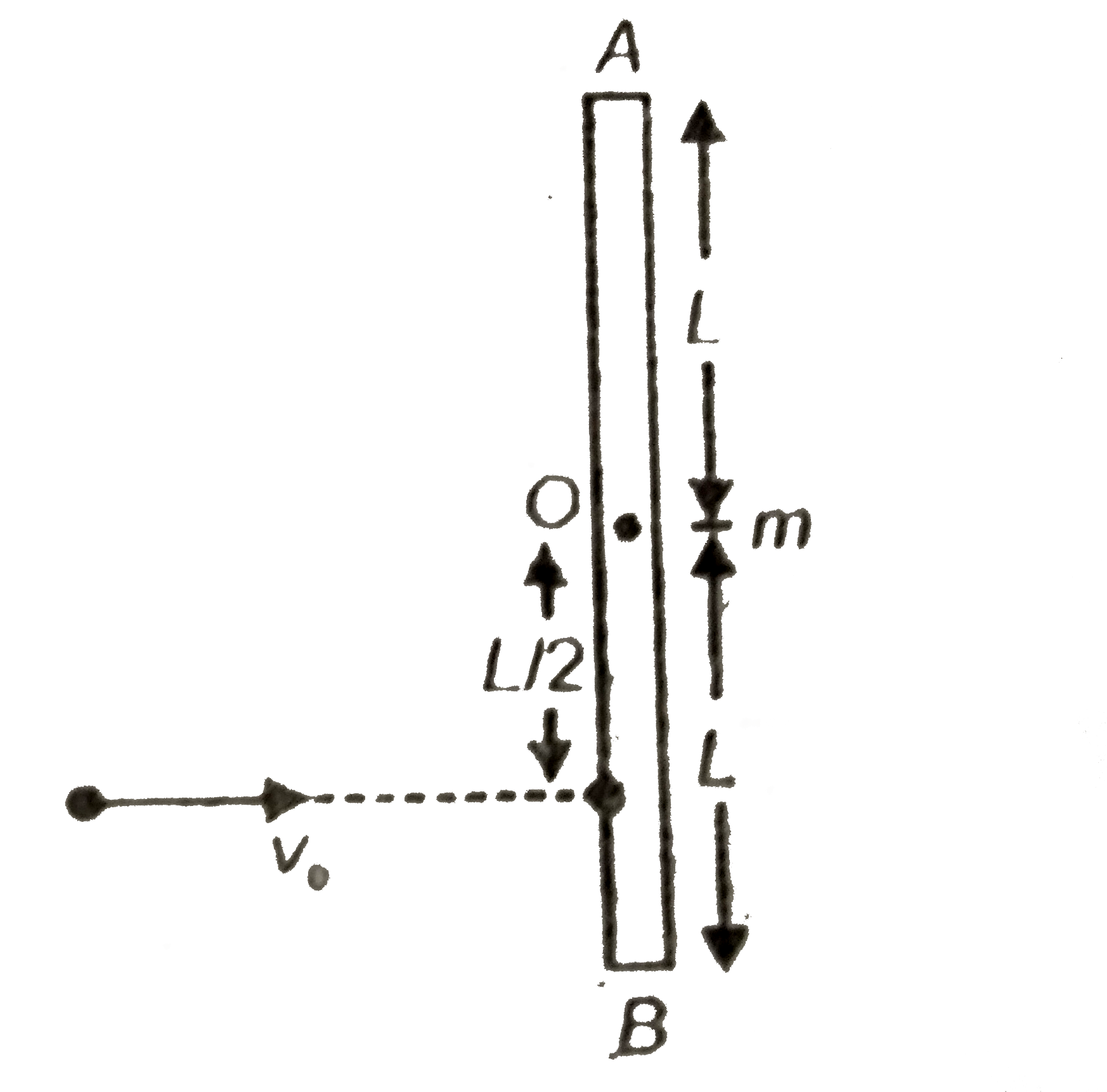
Distance of point P on rod from B which is at rest immediately afte collision is
View SolutionWhen a particle is projected at some angle with the horizontal, the path of the particle is parabolic. In the process the horizontal velocity remains constant but the magnitude of vertical velocity changes. At any instant during flight the acceleration of the particle remains g in vertically downward direction. During flight at any point the path of particle can be considered as a part of circle and radius of that circle is called the radius of curvature of the path
Consider that a particle is projected with velocity u=10m/s at an angle θ=60∘ with the horizontal and take value of g=10m/s2. Now answer the following questions.
The radius of curvature of path of particle at the instant when the velocity vector of the particle becomes perpendicular to initial velocity vector is
View SolutionTangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
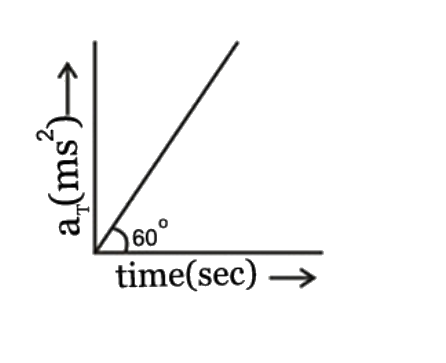
View SolutionA projectile projected with initial velocity 20m/s and at and angle of 30∘ from horizontal. Find the total work done when it will hit the ground.
View SolutionA body is projected with an initial velocity of 58.8 m/s at angle 60° with the vertical. The vertical component of velocity after 2 sec is
View SolutionFind the ratio of de Broglie wavelengths of proton and α-particle of same energy
View Solution
