Question

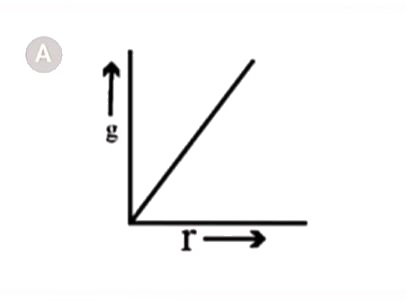
If the density of a planet is constant, then the curve between value of g on its surface and its radius r will be-

Options

A.
B.
C.
D.

Answer

A

Explanation

To solve the problem, we need to establish the relationship between the gravitational acceleration $$g$$ at the surface of a planet and its radius $$r$$, given that the density of the planet is constant.

1. Understanding the relationship: The gravitational acceleration \( g \) at the surface of a planet is given by the formula:
\( g = \frac{G \cdot M}{R^2} \)
where \( G \) is the gravitational constant, \( M \) is the mass of the planet, and \( R \) is the radius of the planet.

2. Expressing mass in terms of density: Since the density \( \rho \) of the planet is constant, we can express the mass \( M \) in terms of density and volume:
\( M = \rho \cdot V \)
The volume \( V \) of a sphere is given by:
\( V = \frac{4}{3} \pi R^3 \)
Therefore, we can write:
\( M = \rho \cdot \frac{4}{3} \pi R^3 \)

3. Substituting mass back into the equation for \( g \): Now, substituting the expression for \( M \) into the equation for \( g \):
\( g = \frac{G \cdot \left(\rho \cdot \frac{4}{3} \pi R^3\right)}{R^2} \)

4. Simplifying the equation: This simplifies to:
\( g = \frac{G \cdot \rho \cdot \frac{4}{3} \pi R^3}{R^2} = \frac{4}{3} \pi G \rho R \)
Here, we can see that \( g \) is directly proportional to \( R \):
\( g \propto R \)

5. Interpreting the relationship: Since \( g \) is directly proportional to \( R \), if we plot \( g \) against \( R \), we will get a straight line that passes through the origin.

Conclusion:
Thus, the curve between the value of \( g \) on the surface of the planet and its radius \( r \) will be a straight line passing through the origin.

Final Answer:
The answer is option A: A straight line passing through the origin.

---