Two blocks A and B of masses 3 kg and 6 kg are connected by a massless spring of force constant 1800 N m−1 and then they are placed on a smooth horizontal surface. The blocks are pulled apart to stretch the spring by 5 cm and then released. What is the relative velocity (in ms−1) of the blocks when the spring comes to its natural length?
The correct Answer is:1.5
To solve the problem, we will use the principles of conservation of energy and conservation of momentum. Here’s the step-by-step solution:
Step 1: Understand the Initial and Final Conditions
Initially, the spring is stretched by x=5cm=0.05m. The potential energy stored in the spring when stretched is given by:
PE=12kx2
where k=1800N/m.
Step 2: Calculate the Initial Potential Energy
Substituting the values into the potential energy formula:
PE=12×1800×(0.05)2
Calculating this gives:
PE=12×1800×0.0025=2.25J
Step 3: Set Up the Conservation of Energy Equation
When the spring returns to its natural length, all the potential energy converts into kinetic energy. The kinetic energy of the two blocks can be expressed as:
KE=12m1v21+12m2v22
where m1=3kg and m2=6kg.
Setting the initial potential energy equal to the total kinetic energy:
2.25=12×3v21+12×6v22
Simplifying this gives:
2.25=32v21+3v22
Multiplying through by 2 to eliminate the fractions:
4.5=3v21+6v22(Equation 1)
Step 4: Use Conservation of Momentum
Since there are no external forces acting on the system, we can apply the conservation of momentum:
m1v1=m2v2
Substituting the masses gives:
3v1=6v2
From this, we can express v1 in terms of v2:
v1=2v2(Equation 2)
Step 5: Substitute Equation 2 into Equation 1
Now substitute v1=2v2 into Equation 1:
4.5=3(2v2)2+6v22
This simplifies to:
4.5=3×4v22+6v22
4.5=12v22+6v22
4.5=18v22
Solving for v22:
v22=4.518=0.25
Taking the square root:
v2=0.5m/s
Step 6: Calculate v1
Using Equation 2:
v1=2v2=2×0.5=1m/s
Step 7: Calculate the Relative Velocity
The relative velocity vrel of block A with respect to block B is given by:
vrel=v1+v2=1+0.5=1.5m/s
Final Answer
The relative velocity of the blocks when the spring comes to its natural length is:
1.5m/s
Initially, the spring is stretched by x=5cm=0.05m. The potential energy stored in the spring when stretched is given by:
PE=12kx2
where k=1800N/m.
Substituting the values into the potential energy formula:
PE=12×1800×(0.05)2
Calculating this gives:
PE=12×1800×0.0025=2.25J
When the spring returns to its natural length, all the potential energy converts into kinetic energy. The kinetic energy of the two blocks can be expressed as:
KE=12m1v21+12m2v22
where m1=3kg and m2=6kg.
2.25=12×3v21+12×6v22
Simplifying this gives:
2.25=32v21+3v22
Multiplying through by 2 to eliminate the fractions:
4.5=3v21+6v22(Equation 1)
Since there are no external forces acting on the system, we can apply the conservation of momentum:
m1v1=m2v2
Substituting the masses gives:
3v1=6v2
From this, we can express v1 in terms of v2:
v1=2v2(Equation 2)
Now substitute v1=2v2 into Equation 1:
4.5=3(2v2)2+6v22
This simplifies to:
4.5=3×4v22+6v22
4.5=12v22+6v22
4.5=18v22
Solving for v22:
v22=4.518=0.25
Taking the square root:
v2=0.5m/s
Using Equation 2:
v1=2v2=2×0.5=1m/s
The relative velocity vrel of block A with respect to block B is given by:
vrel=v1+v2=1+0.5=1.5m/s
The relative velocity of the blocks when the spring comes to its natural length is:
1.5m/s
Similar Questions
Two blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks A and B of masses 5kg and 2kg respectively connected by a spring of force constant =100Nm−1 are placed on an inclined plane of inclined 30∘ as shown in figure If the system is released from rest
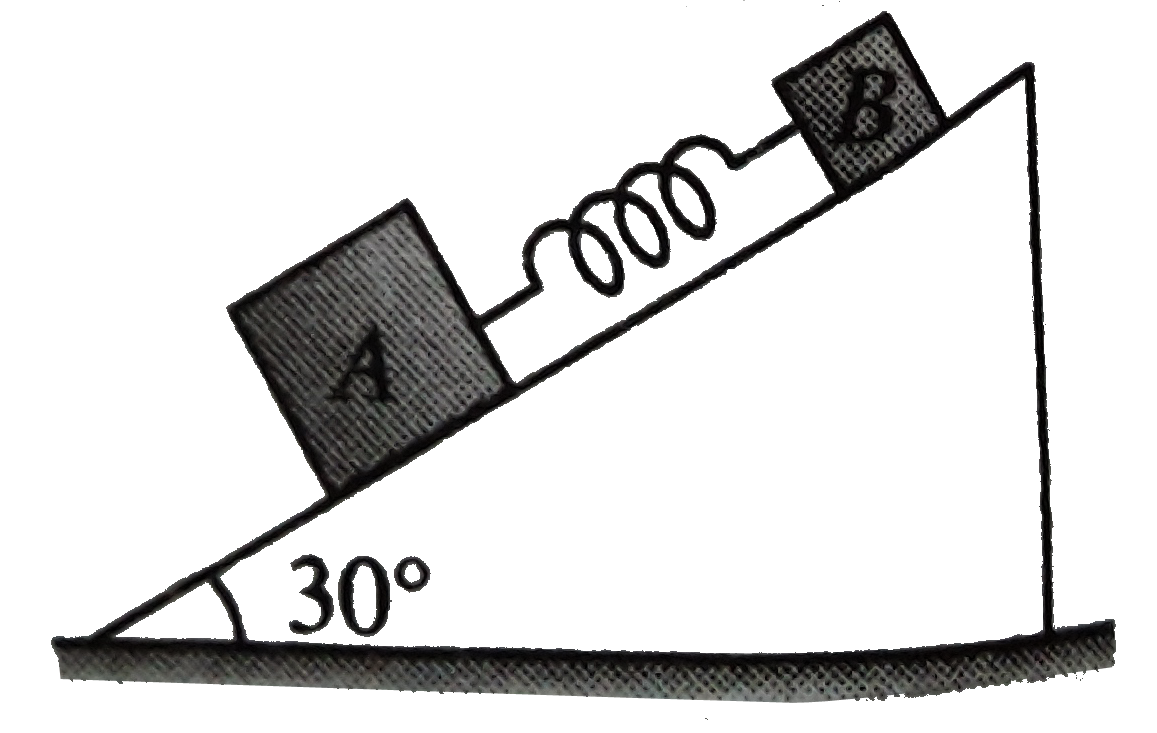
View Solution
Knowledge Check
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400N
Two uniform discs A and B of equal radii but having different masses 1 kg and 2 kg respectively, are connected (at centres) by a massless spring of spring constant k=1000Nm−1 and then placed on a sufficiently rough horizontal surface. If initially, the system is released from rest with the spring being compressed by 10 cm, then the speed of A when the spring comes back to its natural length, is

View SolutionTwo blocks A and B of masses 1kg and 2kg are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Find the ratio of their,
(a) speed
(b) magnitude of momentum and
(c) kinetic energy at any instant.
View SolutionTwo blocks A and B of masses mA and mB are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Show that the kinetic energies of the blocks are, at any instant inversely proportional to their masses.
View SolutionTwo blocks of masses 6 kg and 3 kg are attached to the two ends of a massless spring of spring constant 2π2N/m. If spring is compressed and released on a smooth horizontal surface then find the time period (in seconds) of each block.
View SolutionTwo blocks of masses 7 kg and 3 kg are connected by a spring of stiffness 1000Nm−1 and placed on a smooth horizontal surface. They are acted by horizontal forces of 72 N and 32 N in opposite directions as shown in the figure. When accelerations of the blocks are equal and constant, the extension of the spring is
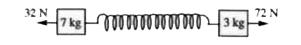
View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of oscillation is
View SolutionTwo block of mass 1kg and 2kg are connected by a string AB of mass 1kg. The blocks are placed on a smooth horizontal surface. Block of mass 1kg is pulled by a horizontal force F of magnitude 8N. Find the tension in the string at points A and B

View Solution
