A thin glass prism of μ=1.5 is immersed in water of μ=1.33 . The ratio of deviation of the ray in water to that in air for the same prism is
1:4
1:2
1:8
1:3
The correct Answer is:A
To solve the problem of finding the ratio of deviation of a ray in water to that in air for a thin glass prism, we can follow these steps:
Step 1: Understand the formula for deviation
The deviation D for a prism can be expressed using the formula:
D=(n−1)⋅A
where n is the relative refractive index of the prism with respect to the medium it is in, and A is the angle of the prism.
Step 2: Calculate the deviation in air
For the prism in air, the refractive index of air is approximately 1. Therefore, the relative refractive index n of the glass prism with respect to air is:
nair=μglassμair=1.51=1.5
Now, substituting this into the deviation formula gives:
Dair=(1.5−1)⋅A=0.5⋅A
Step 3: Calculate the deviation in water
For the prism immersed in water, the refractive index of water is given as 1.33. Thus, the relative refractive index n of the glass prism with respect to water is:
nwater=μglassμwater=1.51.33
Now substituting this into the deviation formula gives:
Dwater=(1.51.33−1)⋅A
Calculating 1.51.33−1:
Dwater=(1.5−1.33)⋅A1.33=0.171.33⋅A
Step 4: Find the ratio of deviations
Now, we can find the ratio of the deviation in water to the deviation in air:
Ratio=DwaterDair=(0.171.33⋅A)(0.5⋅A)
The A cancels out:
Ratio=0.171.33⋅0.5=0.170.665
Calculating this gives:
Ratio≈0.255
Step 5: Approximate the ratio
To express this as a fraction:
Ratio≈13
Final Answer
Thus, the ratio of the deviation of the ray in water to that in air for the same prism is approximately:
13
The deviation D for a prism can be expressed using the formula:
D=(n−1)⋅A
where n is the relative refractive index of the prism with respect to the medium it is in, and A is the angle of the prism.
For the prism in air, the refractive index of air is approximately 1. Therefore, the relative refractive index n of the glass prism with respect to air is:
nair=μglassμair=1.51=1.5
Now, substituting this into the deviation formula gives:
Dair=(1.5−1)⋅A=0.5⋅A
For the prism immersed in water, the refractive index of water is given as 1.33. Thus, the relative refractive index n of the glass prism with respect to water is:
nwater=μglassμwater=1.51.33
Now substituting this into the deviation formula gives:
Dwater=(1.51.33−1)⋅A
Calculating 1.51.33−1:
Dwater=(1.5−1.33)⋅A1.33=0.171.33⋅A
Now, we can find the ratio of the deviation in water to the deviation in air:
Ratio=DwaterDair=(0.171.33⋅A)(0.5⋅A)
The A cancels out:
Ratio=0.171.33⋅0.5=0.170.665
Calculating this gives:
Ratio≈0.255
To express this as a fraction:
Ratio≈13
Thus, the ratio of the deviation of the ray in water to that in air for the same prism is approximately:
13
Similar Questions
A thin lens (μ=1.5) of focal length + 12 cm is immersed in water (μ=1.33). What is its new focal length ?
View SolutionA thin prism of angle 6.0∘,ω'=0.07andμy'=1.50 is combined with another thin prism having ω=0.08andμy=1.60. The combination produces no deviation in the mean ray. (a) Find the angle of the second prism. (b) Find the net angular dispersion produced by the combination when a beam of white light passes through it. (c) If the prisms are similarly directed, what will be the deviation in the mean ray ? (d) Find the angular dispersion in the situation described in (c).
View Solution
Knowledge Check
A convex lens of focal legnth 0.2m and made of glass (μ=1.50) is immersed in water (μ=1.33). Find the change in the focal length of the lens.
A5.8mB0.58cmC0.58mD5.8cmA thin prism of angle 15∘ made of glass of refractive index μ1=1.5 is combined with another prism of glass of refractive index μ2=1.75. The combination of the prism produces dispersion without deviation. The angle of the second prism should be
A5∘B7∘C10∘D12∘
A prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. By rotating the prism, the minimum angle of deviation is measured to be 40∘. What is the refractive index of the prism ? If the prism is placed in water (μ=1.33), predict the new angle of minimum deviation of the parallel beam. The refracting angle of prism is 60∘.
View Solution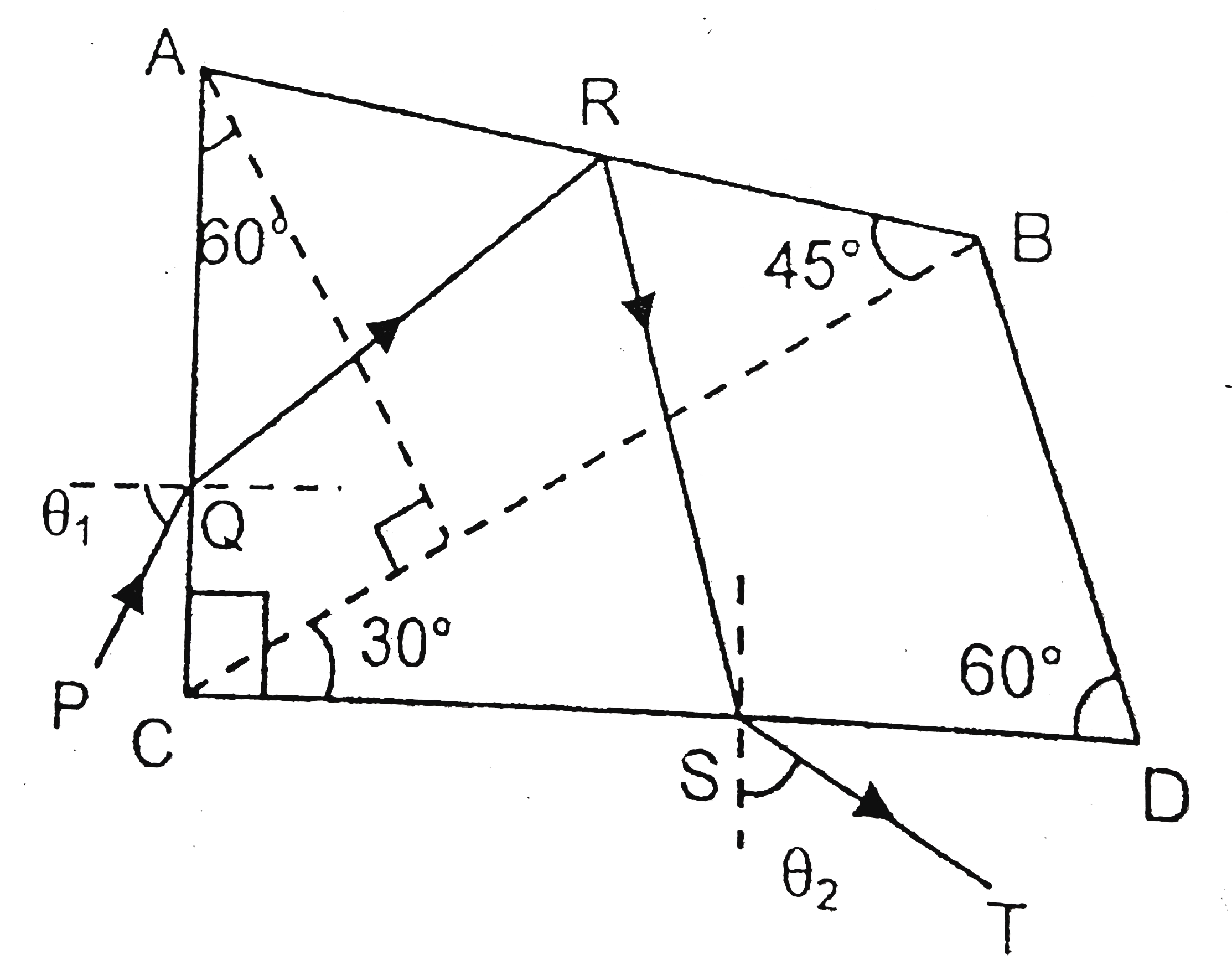
The figure shows a constant deviation prism ABCD. The incident ray is PQ and the emergent ray is ST. Although it is made up of one piece of glass, but it is equivalent to two 30∘−60∘−90∘ prism and one 45∘−45∘90∘ prism.The angle θ1 is the angle of incidence on face AB. The path of the ray inside the prism is indicated in the figure. for this prism μ=2sinθ1.
Q. The total deviation of incident ray when it emerges out of the prism is
View SolutionA concave mirror of focal length f (in air) is immersed in water (μ=4/3). The focal length of the mirror in water will be
View SolutionA glass prism of refractive index 1.5 is immersed in water of refractive index 4/3. A light ray incident normally on face AB is totally reflected at face AC if

View SolutionA flint glass prism and a crown glass prism are to be combined in such a way that the deviation of the mean ray is zero. The refractive index of flint and crown glasses for the mean ray are 1.620 and 1.518 respectively. If the refracting angle of the flint prism is 6.0∘, what would be the refracting angle of the crown prism ?
View SolutionA equilateral prism of flint glass (μg=3/2) is placed water (μw=4/3).
At what angle should a ray of light fall on the face of the prism so that inside the prism the ray is perpendicular to the bisector of the angle of the prism.
Through what angle will the ray turn after passing through both faces of the prism?
View Solution
