A uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
√10g(R+r)17r2
√10g(R−r)17r2
√10g(R+r)17
√10(R+r)17
The correct Answer is:A
To find the angular velocity of a uniform ball of radius r rolling without slipping down from the top of a sphere of radius R at the moment it breaks off, we can follow these steps:
Step 1: Understand the Geometry of the Problem
The ball rolls down the sphere and breaks off at an angle θ with the vertical. The distance from the center of the sphere to the center of the ball when it breaks off is R+r.
Step 2: Apply Energy Conservation
Initially, the ball is at rest at height h=R+r. As it rolls down, it gains kinetic energy. The potential energy lost is converted into kinetic energy. The height h at the moment it breaks off can be expressed as:
h=(R+r)−(R+r)cosθ=(R+r)(1−cosθ)
Step 3: Write the Energy Conservation Equation
Using the work-energy theorem, the work done by gravity equals the change in kinetic energy:
mgh=K.E.
The kinetic energy consists of translational and rotational parts:
mgh=12mv2+12Iω2
For a uniform ball, the moment of inertia I is given by 25mr2. The relationship between linear velocity v and angular velocity ω is v=rω.
Step 4: Substitute and Simplify
Substituting I and ω:
mgh=12mv2+12(25mr2)(v2r2)
This simplifies to:
mgh=12mv2+15mv2=710mv2
Cancelling m from both sides gives:
gh=710v2
Step 5: Substitute for h
Substituting for h:
g(R+r)(1−cosθ)=710v2
From this, we can express v2:
v2=10g(R+r)(1−cosθ)7
Step 6: Centripetal Force Condition
At the point of breaking off, the centripetal force required for circular motion is provided by the component of the gravitational force acting on the ball. The equation is:
mgcosθ=mv2R+r
Cancelling m gives:
gcosθ=v2R+r
Substituting for v2:
gcosθ=10g(R+r)(1−cosθ)7(R+r)
This simplifies to:
cosθ=10(1−cosθ)7
Solving for cosθ:
7cosθ=10−10cosθ
17cosθ=10⟹cosθ=1017
Step 7: Calculate v
Substituting cosθ back into the equation for v2:
v2=10g(R+r)(1−1017)7=10g(R+r)(717)7=10g(R+r)17
Step 8: Find Angular Velocity ω
Using v=rω:
ω=vr=√10g(R+r)17r=√10g(R+r)17r2
Final Answer
The angular velocity ω of the ball at the moment it breaks off the sphere is:
ω=√10g(R+r)17r2
The ball rolls down the sphere and breaks off at an angle θ with the vertical. The distance from the center of the sphere to the center of the ball when it breaks off is R+r.
Initially, the ball is at rest at height h=R+r. As it rolls down, it gains kinetic energy. The potential energy lost is converted into kinetic energy. The height h at the moment it breaks off can be expressed as:
h=(R+r)−(R+r)cosθ=(R+r)(1−cosθ)
Using the work-energy theorem, the work done by gravity equals the change in kinetic energy:
mgh=K.E.
The kinetic energy consists of translational and rotational parts:
mgh=12mv2+12Iω2
For a uniform ball, the moment of inertia I is given by 25mr2. The relationship between linear velocity v and angular velocity ω is v=rω.
Substituting I and ω:
mgh=12mv2+12(25mr2)(v2r2)
This simplifies to:
mgh=12mv2+15mv2=710mv2
Cancelling m from both sides gives:
gh=710v2
Substituting for h:
g(R+r)(1−cosθ)=710v2
From this, we can express v2:
v2=10g(R+r)(1−cosθ)7
At the point of breaking off, the centripetal force required for circular motion is provided by the component of the gravitational force acting on the ball. The equation is:
mgcosθ=mv2R+r
Cancelling m gives:
gcosθ=v2R+r
Substituting for v2:
gcosθ=10g(R+r)(1−cosθ)7(R+r)
This simplifies to:
cosθ=10(1−cosθ)7
Solving for cosθ:
7cosθ=10−10cosθ
17cosθ=10⟹cosθ=1017
Substituting cosθ back into the equation for v2:
v2=10g(R+r)(1−1017)7=10g(R+r)(717)7=10g(R+r)17
Using v=rω:
ω=vr=√10g(R+r)17r=√10g(R+r)17r2
The angular velocity ω of the ball at the moment it breaks off the sphere is:
ω=√10g(R+r)17r2
Similar Questions
A uniform ball of radius r is placed on the top of a sphere of radius R = 10 r. It is given a slight push due to which it starts rolling down the sphere without slipping. The spin angular velocity of the ball when it breaks off from the sphere is ω=√pq(gr), where g is the acceleration due to gravity and p and q are the smallest integers. What is the value of p+q?
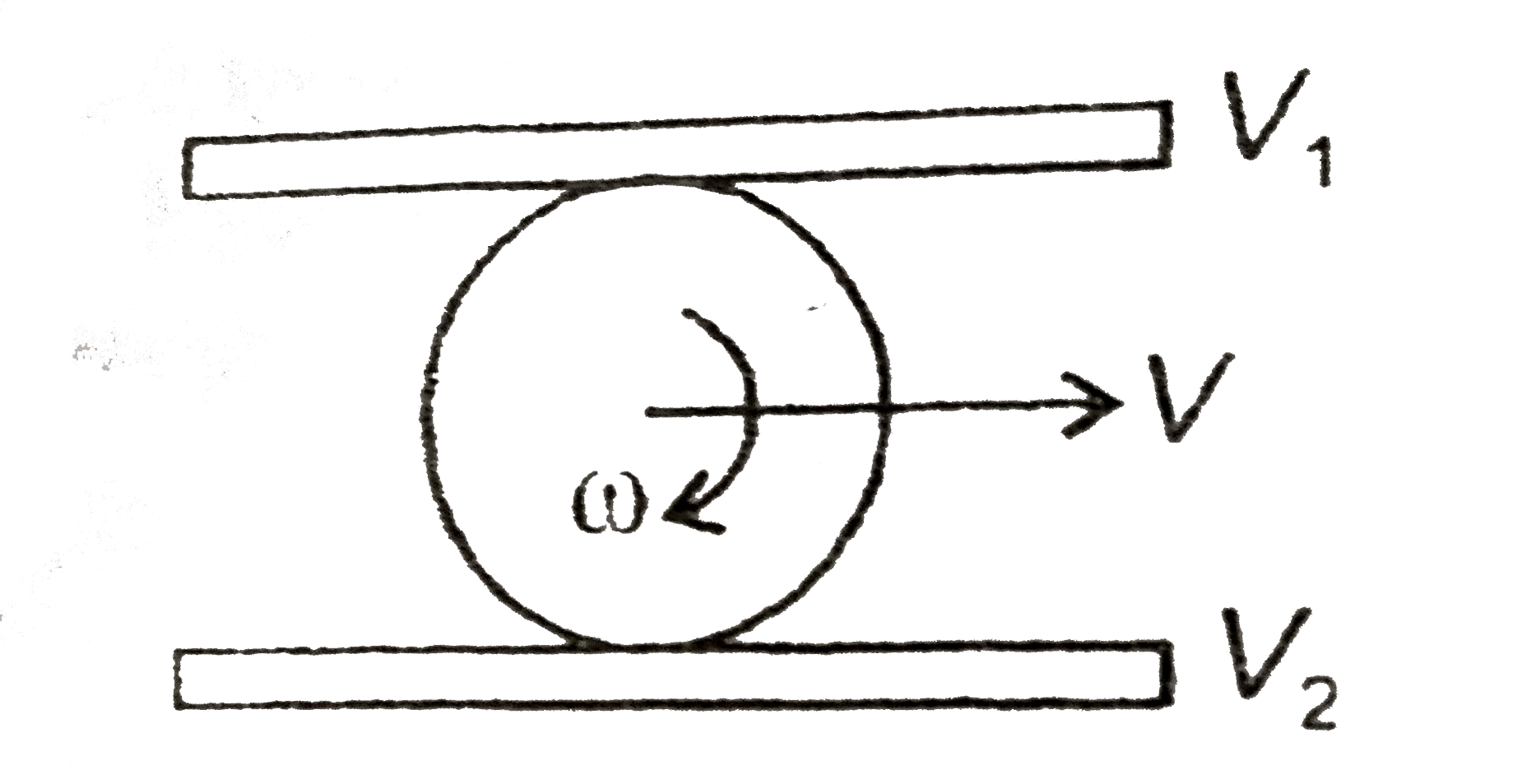
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View SolutionA uniform ball of radius R rolls without slipping between the rails such that the horizontal distance is √3R between the two contact points of te rails of the ball. Figure (a) shows front view of the ball and figure (b) shows the side view of the ball. vCM is the velocity of centre of mass of the ball and ω is the angular velocity of the ball after rolling down a distance 2h along the incline then
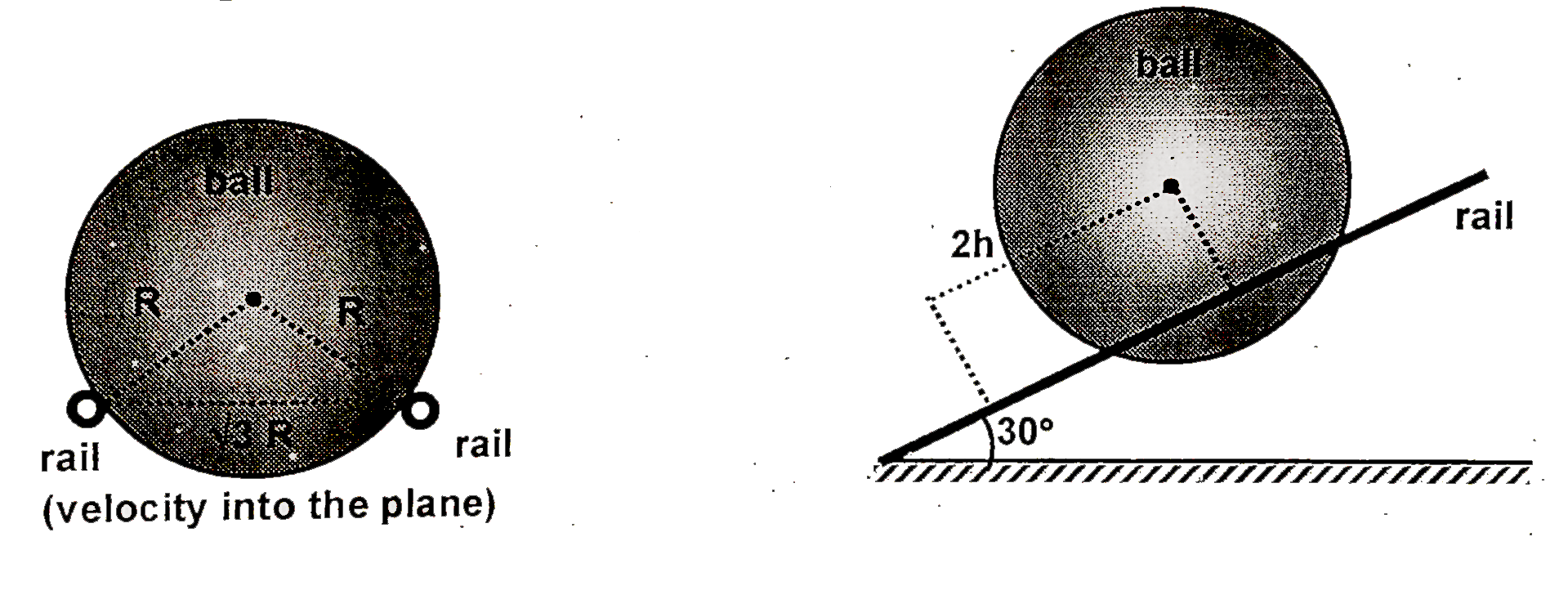
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If its radius is R, then the angular momentum of the sphere about the point of contact is.
View Solution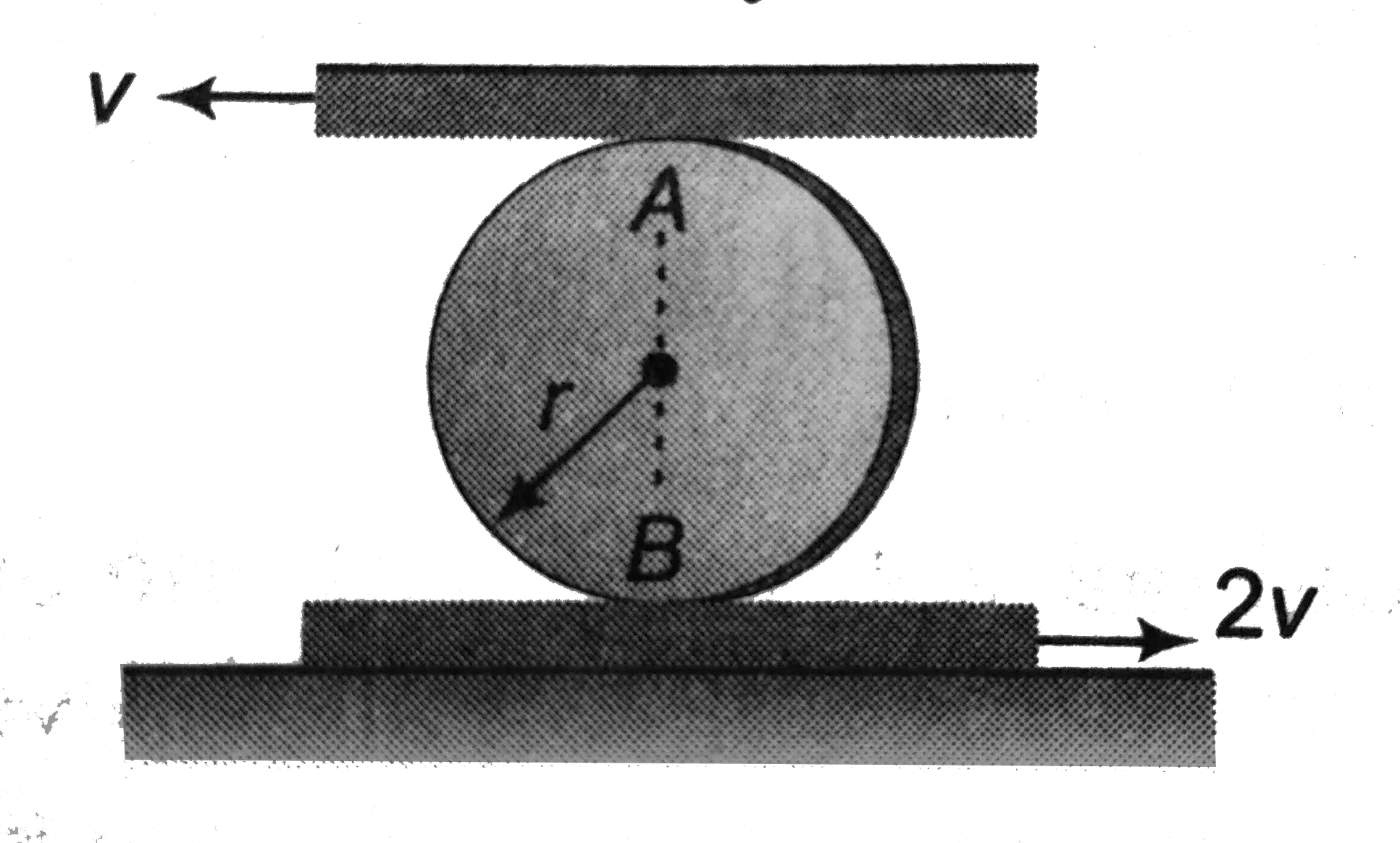
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View SolutionA disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is

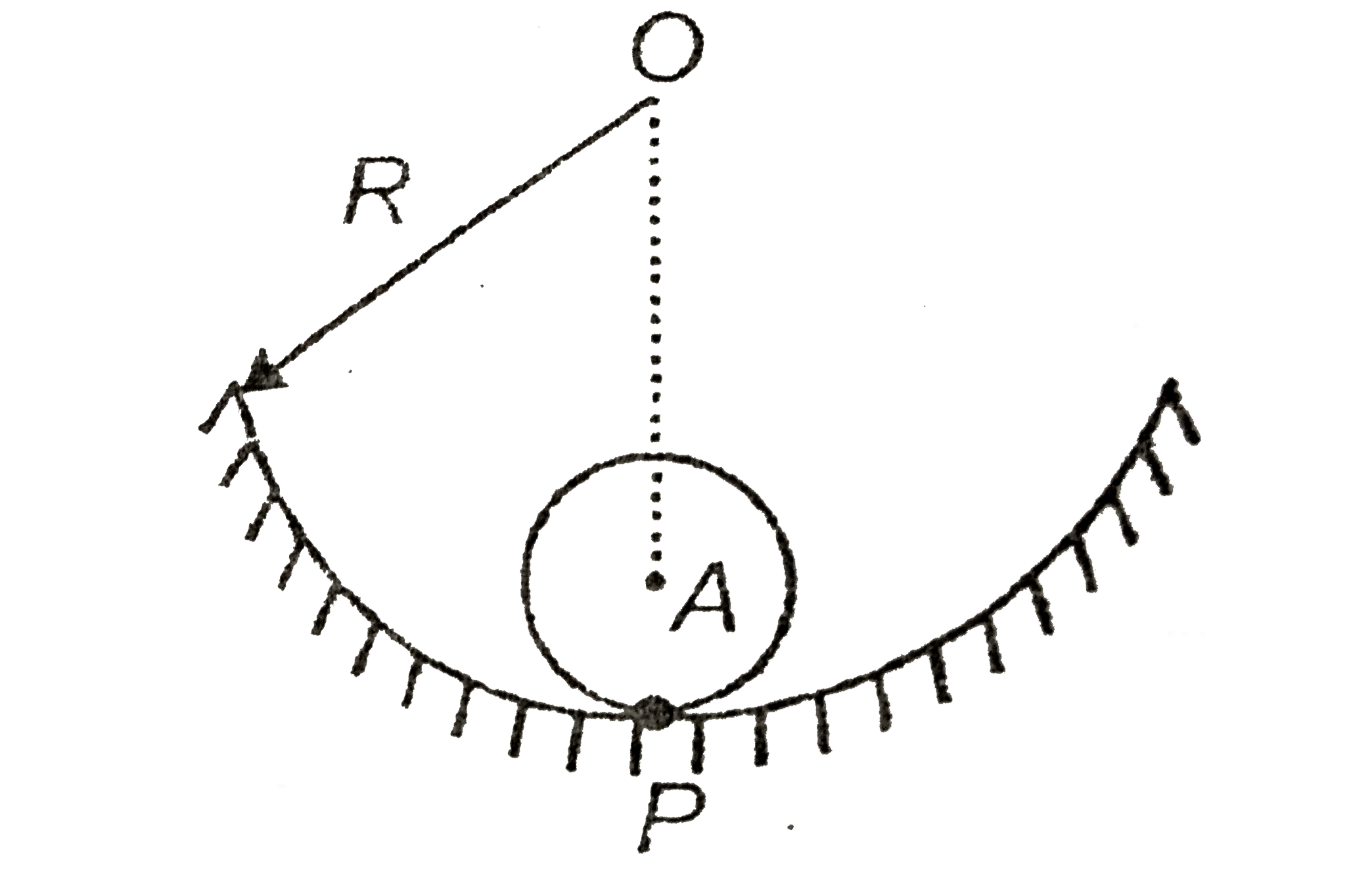
View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
View SolutionIn order to get a billiard ball to roll without sliding from the start, where should the cue hit ? Calculate the height from centre of the sphere. Take R as the radius of sphere.
View SolutionA solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

View Solution
