A uniform ball of radius r is placed on the top of a sphere of radius R = 10 r. It is given a slight push due to which it starts rolling down the sphere without slipping. The spin angular velocity of the ball when it breaks off from the sphere is ω=√pq(gr), where g is the acceleration due to gravity and p and q are the smallest integers. What is the value of p+q?
The correct Answer is:127
To solve the problem, we will analyze the motion of a uniform ball rolling down a larger sphere. We will derive the spin angular velocity of the ball when it breaks off from the sphere.
1. Understanding the Setup:
- We have a uniform ball of radius r placed on top of a sphere of radius R=10r.
- The ball is given a slight push and starts rolling down the sphere without slipping.
2. Conservation of Energy:
- When the ball rolls down, it loses potential energy and gains kinetic energy.
- The potential energy lost when the ball descends from height h is given by:
ΔPE=mgH
- The height H can be expressed in terms of the angle θ as:
H=R−Rcosθ=R(1−cosθ)=10r(1−cosθ)
- Thus, the potential energy lost becomes:
ΔPE=mg⋅10r(1−cosθ)
3. Kinetic Energy:
- The total kinetic energy when the ball is rolling down consists of translational and rotational components:
KE=12mv2+12Iω2
- For a solid sphere, the moment of inertia I is given by:
I=25mr2
- Using the rolling condition v=rω, we can express ω in terms of v:
ω=vr
- Substituting ω into the kinetic energy equation gives:
KE = \frac{1}{2} mv^2 + \frac{1}{2} \left(\frac{2}{5} m r^2\right \left(\frac{v}{r}\right)^2 = \frac{1}{2} mv^2 + \frac{1}{5} mv^2 = \frac{7}{10} mv^2
4. Setting Up the Energy Equation:
- Equating the potential energy lost to the kinetic energy gained:
mg⋅10r(1−cosθ)=710mv2
- Canceling m from both sides:
g⋅10r(1−cosθ)=710v2
5. Centripetal Force Condition:
- At the point of breaking off, the normal force N becomes zero. The gravitational force component providing centripetal acceleration is:
mgcosθ=mv2R
- Substituting R=11r:
mgcosθ=mv211r
- Canceling m:
gcosθ=v211r
6. Substituting for v2:
- From the energy equation, we can express v2:
v2=10g(1−cosθ)7⋅10r
- Substituting this into the centripetal force equation:
gcosθ=10g(1−cosθ)711r
7. Solving for cosθ:
- Rearranging gives:
11gcosθ=10g(1−cosθ)7
- Multiplying through by 7:
77gcosθ=10g−10gcosθ
- Combining terms:
87gcosθ=10g
- Thus:
cosθ=1087
8. Finding ω:
- Substitute cosθ back into the expression for v2:
v2=10g(1−1087)7⋅10r
- Simplifying gives:
v2=10g⋅77877⋅10r
- Finally, substituting v=rω:
r2ω2=10g⋅77877⋅10r
- Solving for ω:
ω2=1100g609r
9. Identifying p and q:
- Comparing with the given form ω=√pqgr:
p=1100,q=609
- Therefore, p+q=1100+609=1709.
Final Answer:
The value of p+q is 1709.
- We have a uniform ball of radius r placed on top of a sphere of radius R=10r.
- The ball is given a slight push and starts rolling down the sphere without slipping.
- When the ball rolls down, it loses potential energy and gains kinetic energy.
- The potential energy lost when the ball descends from height h is given by:
ΔPE=mgH
- The height H can be expressed in terms of the angle θ as:
H=R−Rcosθ=R(1−cosθ)=10r(1−cosθ)
- Thus, the potential energy lost becomes:
ΔPE=mg⋅10r(1−cosθ)
- The total kinetic energy when the ball is rolling down consists of translational and rotational components:
KE=12mv2+12Iω2
- For a solid sphere, the moment of inertia I is given by:
I=25mr2
- Using the rolling condition v=rω, we can express ω in terms of v:
ω=vr
- Substituting ω into the kinetic energy equation gives:
KE = \frac{1}{2} mv^2 + \frac{1}{2} \left(\frac{2}{5} m r^2\right \left(\frac{v}{r}\right)^2 = \frac{1}{2} mv^2 + \frac{1}{5} mv^2 = \frac{7}{10} mv^2
- Equating the potential energy lost to the kinetic energy gained:
mg⋅10r(1−cosθ)=710mv2
- Canceling m from both sides:
g⋅10r(1−cosθ)=710v2
- At the point of breaking off, the normal force N becomes zero. The gravitational force component providing centripetal acceleration is:
mgcosθ=mv2R
- Substituting R=11r:
mgcosθ=mv211r
- Canceling m:
gcosθ=v211r
- From the energy equation, we can express v2:
v2=10g(1−cosθ)7⋅10r
- Substituting this into the centripetal force equation:
gcosθ=10g(1−cosθ)711r
- Rearranging gives:
11gcosθ=10g(1−cosθ)7
- Multiplying through by 7:
77gcosθ=10g−10gcosθ
- Combining terms:
87gcosθ=10g
- Thus:
cosθ=1087
- Substitute cosθ back into the expression for v2:
v2=10g(1−1087)7⋅10r
- Simplifying gives:
v2=10g⋅77877⋅10r
- Finally, substituting v=rω:
r2ω2=10g⋅77877⋅10r
- Solving for ω:
ω2=1100g609r
- Comparing with the given form ω=√pqgr:
p=1100,q=609
- Therefore, p+q=1100+609=1709.
The value of p+q is 1709.
Similar Questions
A uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionA uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionIf g is the acceleration due to gravity and R is the radius of earth, then the dimensional formula for g R is
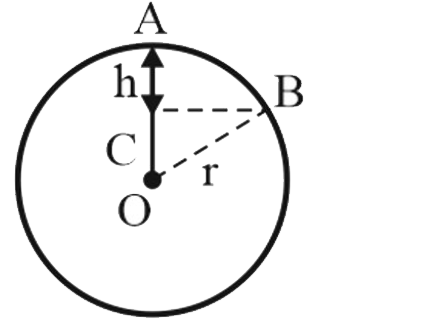
View SolutionIn figure, a particle is placed at the highest point A of a smooth sphere of radius r. It is given slight push, and it leaves the sphere at B, at a depth h vertically below A. The value of h is
View SolutionThe height at which the acceleration due to gravity becomes g9 (where g =the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :
View SolutionThe height at which the acceleration due to gravity becomes g9 (where g =the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :
View SolutionA particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
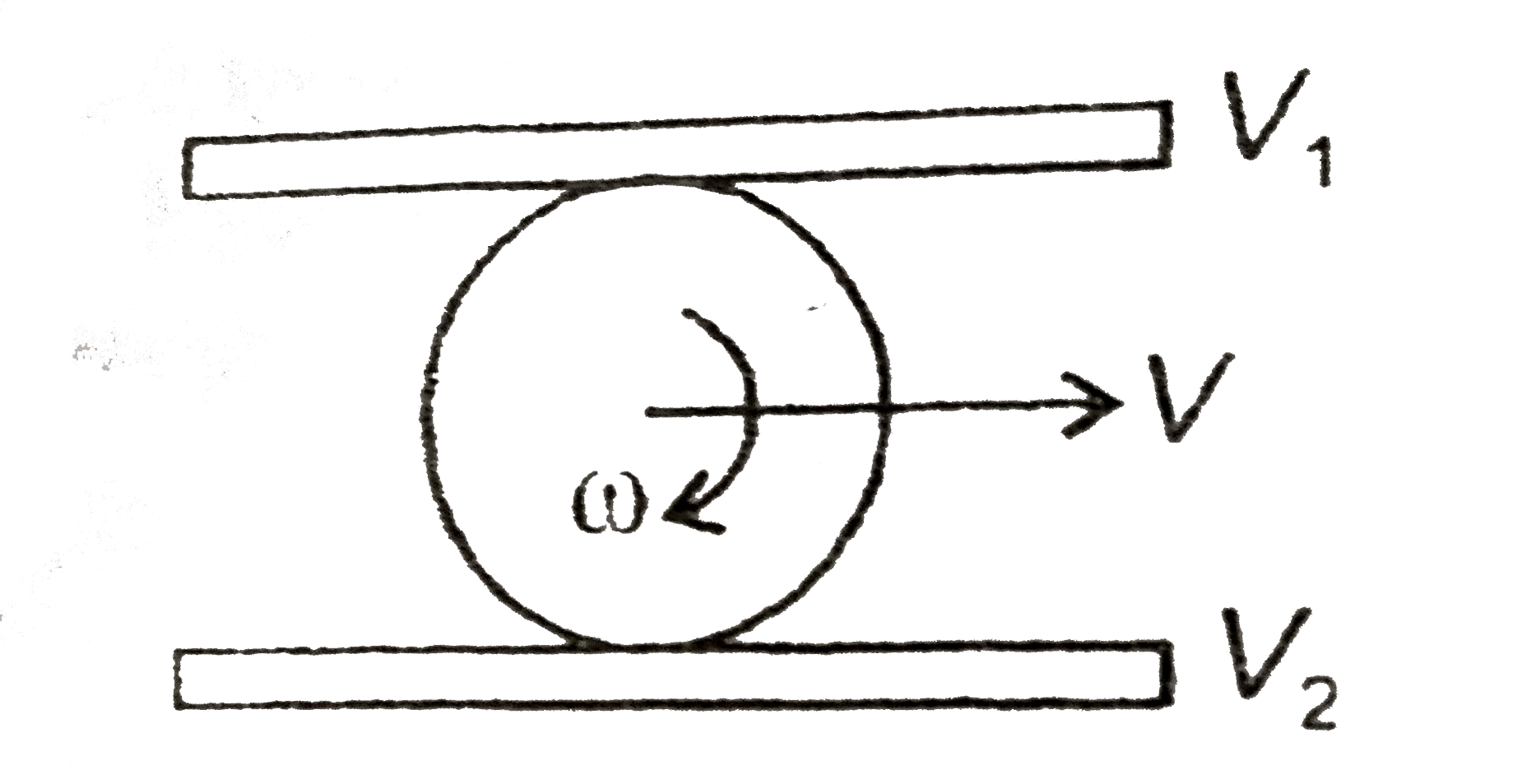
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View SolutionIf earth is supposed to be sphere of radius R, if g20 is value of acceleration due to gravity at latitude of 30∘ and g at the equator, then value of g−g30∘ is
View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View Solution
