A boy of mass 50 kg is climbing a vertical pole at a constant speed. If coefficient of fricition between his palms and the pole is 0.75, then the normal reaction between him and the pole is (take g =10m/s2)
700 N
625.67 N
550 N
666.67 N
The correct Answer is:D
To solve the problem, we need to find the normal reaction force (N) between the boy and the vertical pole as he climbs at a constant speed.
1. Identify the Forces Acting on the Boy:
- The weight of the boy (W) acting downwards:
W=mg
where m=50kg and g=10m/s2.
- The frictional force (F_f) acting upwards, which is responsible for counteracting the weight of the boy.
- The normal reaction force (N) exerted by the pole on the boy's palms.
2. Calculate the Weight of the Boy:
W=mg=50kg×10m/s2=500N
3. Understand the Motion:
- Since the boy is climbing at a constant speed, the net force acting on him is zero. Therefore, the upward frictional force must equal the downward weight:
Ff=W
Ff=500N
4. Relate Frictional Force to Normal Reaction Force:
- The frictional force can be expressed in terms of the normal reaction force (N) and the coefficient of friction (μ):
Ff=μN
where μ=0.75.
5. Set Up the Equation:
- From the previous equations, we have:
500N=0.75N
6. Solve for Normal Reaction Force (N):
N=500N0.75=5000.75=666.67N
Final Answer:
The normal reaction force (N) between the boy and the pole is 666.67N.
---
- The weight of the boy (W) acting downwards:
W=mg
where m=50kg and g=10m/s2.
- The frictional force (F_f) acting upwards, which is responsible for counteracting the weight of the boy.
- The normal reaction force (N) exerted by the pole on the boy's palms.
W=mg=50kg×10m/s2=500N
- Since the boy is climbing at a constant speed, the net force acting on him is zero. Therefore, the upward frictional force must equal the downward weight:
Ff=W
Ff=500N
- The frictional force can be expressed in terms of the normal reaction force (N) and the coefficient of friction (μ):
Ff=μN
where μ=0.75.
- From the previous equations, we have:
500N=0.75N
N=500N0.75=5000.75=666.67N
The normal reaction force (N) between the boy and the pole is 666.67N.
Similar Questions
If coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
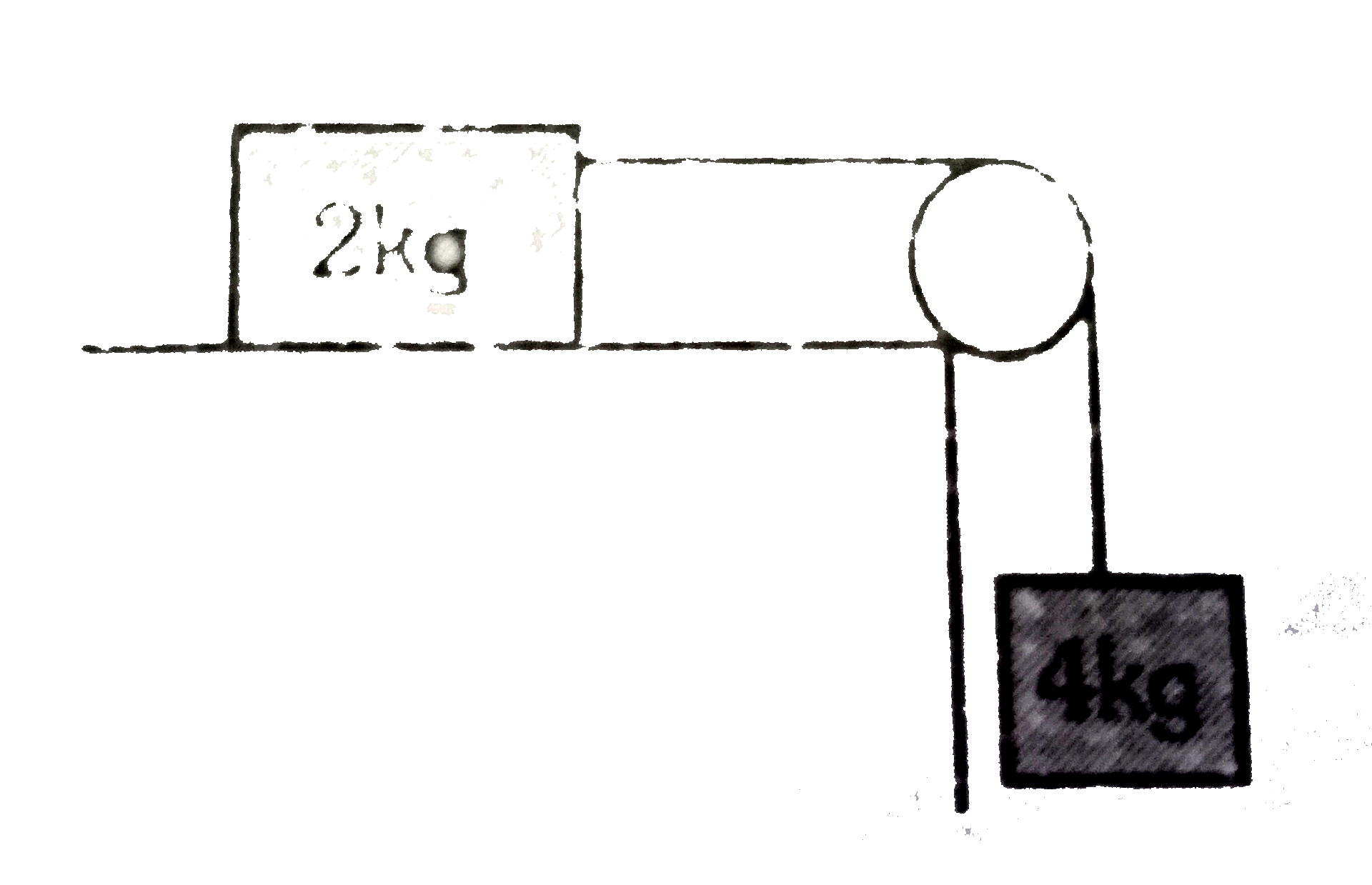
View SolutionA fireman of mass 60 kg slides down a pole. He is pressing the pole with a force of 600N. The coefficient of friction between the hands and the pole is 0.5, with what acceleration will the fireman slide down (g=10ms2)
View SolutionA car is moving on a horizontal circular road of radius 0.1 km with constant speed. If coefficient of friction between tyres of car and road is 0.4, then speed of car may be (g=10m/s2)
View SolutionA car is moving on a horizontal circular track of radius 0.2 km with a constant speed. If coefficient of friction between tyres of car and road is 0.45, then maximum speed of car may be [Take g=10m/s2]
View SolutionIf the system is in equilibrum, find the Normal Reaction between 2kg and 4 kg blocks in Newton. (Take g = 10 m/sec2)

View SolutionA cylinder of 10 kg is sliding in a plane with an initial velocity of 10 m / s . If the coefficient of friction between the surface and cylinder is 0.5 then before stopping, it will cover. (g=10m/s2)
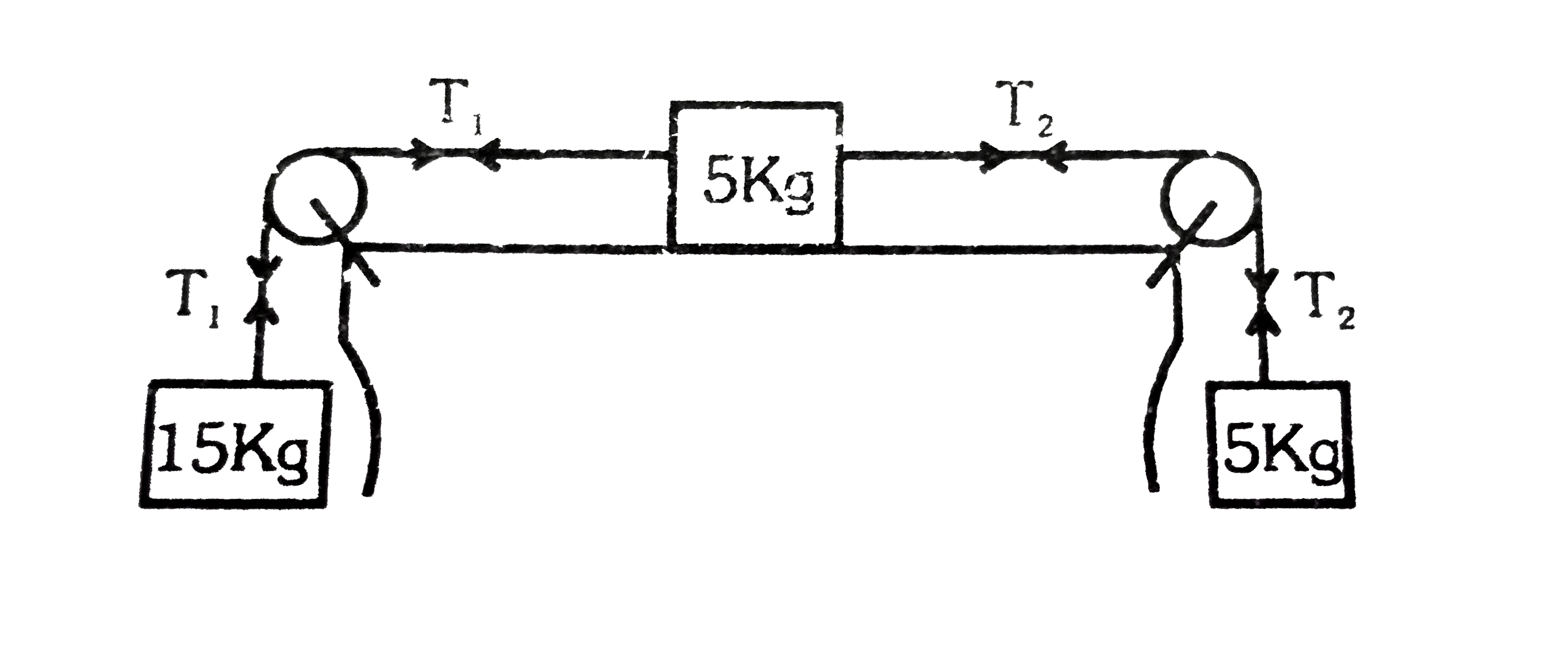
View SolutionThe fricition coefficient between the table and block shown in fig. is 0.2 find the acceleration of the system (Take g=10m/s2)
View SolutionA block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionA constant horizontal force of 5N in magnitude is applied tangentially to the top most of a ring of mass 10 kg and radius 10 cm kept on a rough horizontal surface with coefficient of friction between surface and ring being 0.2. The friction force on the ring would be: (g=10m/s2)
View Solution
