A cylinder of 10 kg is sliding in a plane with an initial velocity of 10 m / s . If the coefficient of friction between the surface and cylinder is 0.5 then before stopping, it will cover.
10m
7.5m
5m
2.5m
The correct Answer is:A
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given data
- Mass of the cylinder (m) = 10 kg
- Initial velocity (u) = 10 m/s
- Coefficient of friction (μ) = 0.5
- Acceleration due to gravity (g) = 10 m/s²
Step 2: Calculate the frictional force
The frictional force (F_f) acting on the cylinder can be calculated using the formula:
Ff=μ⋅m⋅g
Substituting the values:
Ff=0.5⋅10kg⋅10m/s2
Ff=0.5⋅100
Ff=50N
Step 3: Calculate the acceleration due to friction
The frictional force causes a deceleration (negative acceleration) on the cylinder. Using Newton's second law:
F=m⋅a
We can rearrange this to find acceleration (a):
a=Ffm
Substituting the values:
a=50N10kg
a=5m/s2
Since this is a deceleration, we will consider it as negative:
a=−5m/s2
Step 4: Use the kinematic equation to find the distance covered before stopping
We will use the kinematic equation:
v2=u2+2as
Where:
- v = final velocity = 0 m/s (when the cylinder stops)
- u = initial velocity = 10 m/s
- a = acceleration = -5 m/s²
- s = distance covered
Rearranging the equation to solve for s:
0=(10)2+2(−5)s
0=100−10s
10s=100
s=10010
s=10m
Final Answer
The cylinder will cover a distance of 10 meters before stopping.
---
- Mass of the cylinder (m) = 10 kg
- Initial velocity (u) = 10 m/s
- Coefficient of friction (μ) = 0.5
- Acceleration due to gravity (g) = 10 m/s²
The frictional force (F_f) acting on the cylinder can be calculated using the formula:
Ff=μ⋅m⋅g
Ff=0.5⋅10kg⋅10m/s2
Ff=0.5⋅100
Ff=50N
The frictional force causes a deceleration (negative acceleration) on the cylinder. Using Newton's second law:
F=m⋅a
We can rearrange this to find acceleration (a):
a=Ffm
a=50N10kg
a=5m/s2
a=−5m/s2
We will use the kinematic equation:
v2=u2+2as
Where:
- v = final velocity = 0 m/s (when the cylinder stops)
- u = initial velocity = 10 m/s
- a = acceleration = -5 m/s²
- s = distance covered
0=(10)2+2(−5)s
0=100−10s
10s=100
s=10010
s=10m
The cylinder will cover a distance of 10 meters before stopping.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-II
112 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - SWOE
44 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
Similar Questions
Block of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-
View SolutionA block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
View SolutionA block of mass 2kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 5s. The coefficient of friction between the block and ice is (g=10 ms−2)
View SolutionBlock of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-
View SolutionA fireman of mass 60 kg slides down a pole. He is pressing the pole with a force of 600N. The coefficient of friction between the hands and the pole is 0.5, with what acceleration will the fireman slide down (g=10ms2)
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionA constant horizontal force of 5N in magnitude is applied tangentially to the top most of a ring of mass 10 kg and radius 10 cm kept on a rough horizontal surface with coefficient of friction between surface and ring being 0.2. The friction force on the ring would be: (g=10m/s2)
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
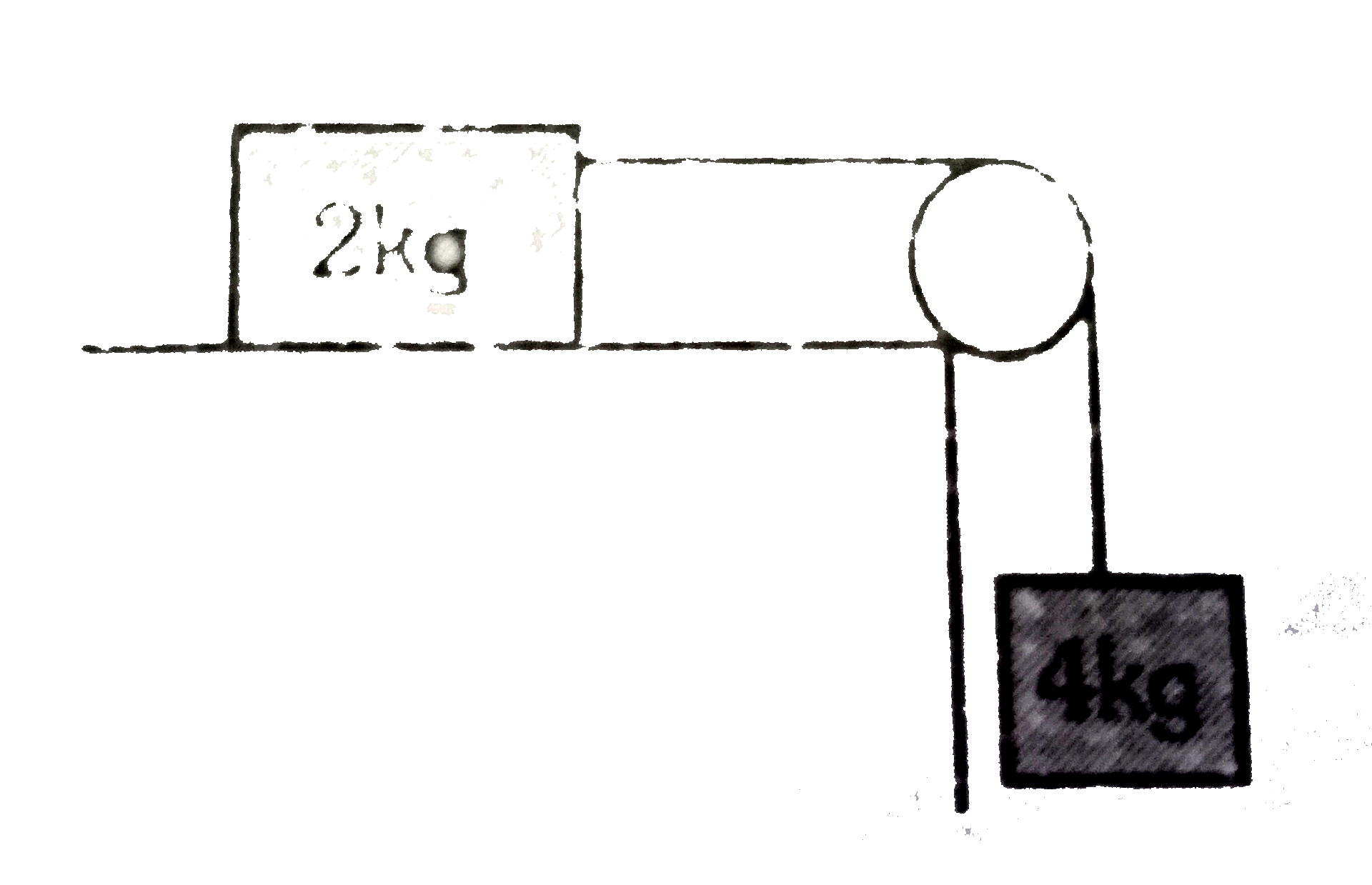
View SolutionA body of mass 2 kg is being dragged with uniform velocity of 2 m / s on a rough horizontal plane. The coefficient of friction between the body and the surface is 0.20. The amount of heat generated in 5 sec is
. (4.2joule/calandg=9.8m/s2)

View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View Solution
