One mole of an ideal gas (CV=20JK−1mol−1) initially at STP is heated at constant volume to twice the initial temeprature. For the process W and q will be
W = 0, q 5.46 kJ
W = 0 , q 0
W = -5.46kJ , q = 5.46 kJ
W = 5.46 kJ , q = 5.46 kJ
The correct Answer is:A
To solve the problem, we need to determine the work done (W) and the heat (q) for the process where one mole of an ideal gas is heated at constant volume from an initial temperature (T1) to twice that temperature (T2).
1. Identify Initial Conditions:
- Given:
- Moles of gas (n) = 1 mole
- Heat capacity at constant volume (C_v) = 20 J/K·mol
- Initial temperature (T1) = 273 K (Standard Temperature)
- Final temperature (T2) = 2 * T1 = 2 * 273 K = 546 K
2. Calculate Change in Temperature (ΔT):
- ΔT = T2 - T1
- ΔT = 546 K - 273 K = 273 K
3. Calculate Work Done (W):
- Since the process occurs at constant volume, the change in volume (ΔV) is 0.
- Work done (W) is given by the formula:
W=PΔV
- Since ΔV = 0, we have:
W=0
4. Calculate Heat (q):
- The heat added (q) during the process at constant volume is given by:
q=nCvΔT
- Substituting the known values:
q=1mol×20J/K⋅mol×273K
- Calculate:
q=20×273=5460J
5. Convert Heat to Kilojoules:
- To convert joules to kilojoules, divide by 1000:
q=54601000=5.46kJ
Final Results:
- Work done (W) = 0 J
- Heat added (q) = 5.46 kJ
- Given:
- Moles of gas (n) = 1 mole
- Heat capacity at constant volume (C_v) = 20 J/K·mol
- Initial temperature (T1) = 273 K (Standard Temperature)
- Final temperature (T2) = 2 * T1 = 2 * 273 K = 546 K
- ΔT = T2 - T1
- ΔT = 546 K - 273 K = 273 K
- Since the process occurs at constant volume, the change in volume (ΔV) is 0.
- Work done (W) is given by the formula:
W=PΔV
- Since ΔV = 0, we have:
W=0
- The heat added (q) during the process at constant volume is given by:
q=nCvΔT
- Substituting the known values:
q=1mol×20J/K⋅mol×273K
- Calculate:
q=20×273=5460J
- To convert joules to kilojoules, divide by 1000:
q=54601000=5.46kJ
- Work done (W) = 0 J
- Heat added (q) = 5.46 kJ
Similar Questions
One mole of ideal gas (CP,m=15JK−1mole−1) follow the process as shown in figure.
View SolutionWhen one mole of an ideal gas is compressed to half of its initial volume and simultaneously heated to twice its initial temperature, the change in entropy of gas (DelataS) is:
View SolutionOne mole of an ideal gas at an initial temperature true of TK does 6R joule of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is 5/3, the final temperature of the gas will be
View SolutionOne mole of an ideal gas at an initial temperature true of TK does 6R joule of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is 5/3, the final temperature of the gas will be
View SolutionOne mole of an ideal gas at 27∘C expanded isothermally from an initial volume of 1 litre to 10 litre. The ΔU for this process is : (R=2calK−1mol−1)
View SolutionOne mole of an ideal gas at 250 K is expanded isothermally from an initial volume of 5 litre to 10 litres. The ΔE for this process is (R=2cal.Mol−1K−1)
View SolutionInitially one mole of ideal gas (Cv=52R) at 0.1 atm and 300 K is put through the following cycle:
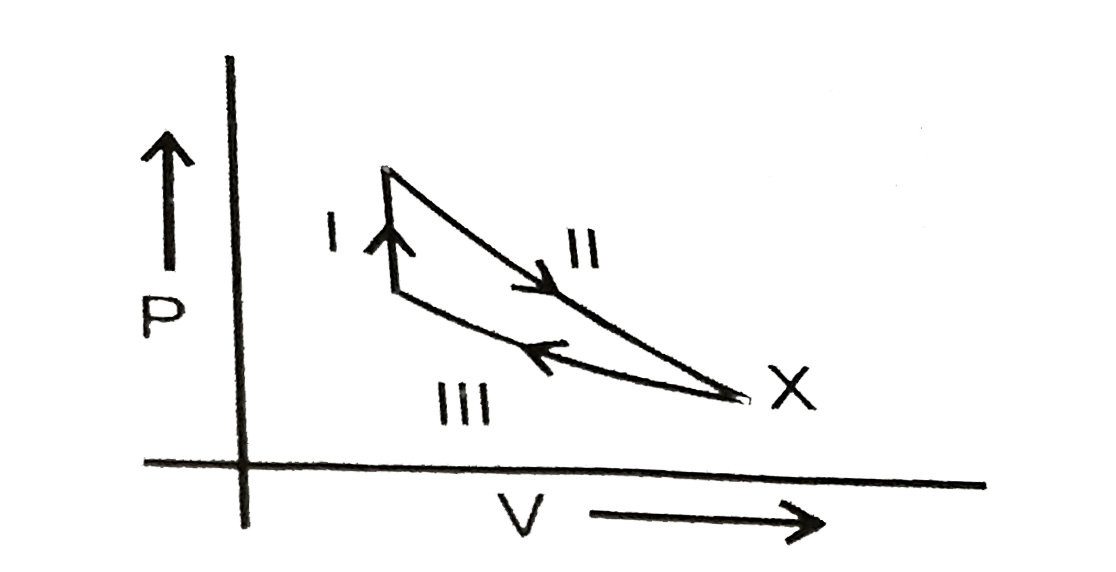
Step-I : Heating to twice its initial pressure at constant volume.
Step-II : Adiabatic expansion to its initial temperature.
Step-III : Isothermal compression back to 1.00 atm.
what is the volume at state X?
View SolutionThree moles of an ideal gas (Cp=72R) at pressure, PA and temperature TA is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original volume. Finally gas is compressed at constant volume to its original pressure PA.
(a) Sketch P-V and P-T diagrams for the complete process.
(b) Calculate the net work done by the gas, and net heat supplied to the gas during the complete process.
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View Solution
