Two long parallel wires are 30 cm apart carrying currents 10 A and 15 A respectively in the same direction. The force acting over a length of 5 m of the wires is
5×10−4N, (attraction)
1×10−4N, (attraction)
5×10−4N, (repulsion)
1×10−4N, (repulsion)
The correct Answer is:A
To solve the problem of finding the force acting on two long parallel wires carrying currents in the same direction, we will follow these steps:
Step 1: Understand the Concept
Two long parallel wires carrying currents in the same direction will exert an attractive force on each other. The formula for the force per unit length between two parallel wires is given by:
F/L=μ0I1I22πR
where:
- F is the force,
- L is the length of the wire,
- μ0 is the permeability of free space (4π×10−7T m/A),
- I1 and I2 are the currents in the wires,
- R is the distance between the wires.
Step 2: Identify the Given Values
From the problem, we have:
- Current in wire 1, I1=10A
- Current in wire 2, I2=15A
- Distance between the wires, R=30cm=0.3m
- Length of the wires considered, L=5m
Step 3: Calculate the Force per Unit Length
Using the formula for force per unit length:
F/L=μ0I1I22πR
Substituting the known values:
F/L=(4π×10−7)×(10)×(15)2π×0.3
Step 4: Simplify the Equation
The π terms cancel out:
F/L=(4×10−7)×(10)×(15)2×0.3
Calculating the numerator:
F/L=(4×10−7)×1500.6
Calculating 4×150=600:
F/L=600×10−70.6
This simplifies to:
F/L=1000×10−7=10−4N/m
Step 5: Calculate the Total Force Over the Length of 5 m
Now, to find the total force acting over a length of 5 m:
F=(F/L)×L=(10−4N/m)×(5m)=5×10−4N
Step 6: Determine the Nature of the Force
Since the currents are in the same direction, the force is attractive.
Final Answer
The force acting over a length of 5 m of the wires is:
5×10−4N (attractive force)
Two long parallel wires carrying currents in the same direction will exert an attractive force on each other. The formula for the force per unit length between two parallel wires is given by:
- F is the force,
- L is the length of the wire,
- μ0 is the permeability of free space (4π×10−7T m/A),
- I1 and I2 are the currents in the wires,
- R is the distance between the wires.
From the problem, we have:
- Current in wire 1, I1=10A
- Current in wire 2, I2=15A
- Distance between the wires, R=30cm=0.3m
- Length of the wires considered, L=5m
Using the formula for force per unit length:
The π terms cancel out:
Now, to find the total force acting over a length of 5 m:
Since the currents are in the same direction, the force is attractive.
The force acting over a length of 5 m of the wires is:
Similar Questions
Knowledge Check
Two parallel wires 2 m apart carry currents of 2 A and 5 A respectively in same direction, the force per unit length acting between these two wires is
A2×10−6Nm−1B3×10−6Nm−1C1×10−6Nm−1D4×10−6Nm−1Two long and parallel straight wires A and B are carrying currents of 4A and 7A in the same directions are separated by a distance of 5cm. The force acting on a 8cm section of wire A is
A3×10−6NB6×10−6NC9×10−6ND12×10−6N
Two infinite, parallel wires are a distance 10 cm apart and carry equal current 20 A in the same direction. The magnetic force on a 1 cm long segment of one wire due to the other wire is ___________ ×10−6N. (Permeabilityi of vacuum μ0=4π×10−7N/A2)
View SolutionTwo long parallel wires placed 0.08 m apart, carry currents 3 A and 5 A in the same direction. what is the distance from the conductor carrying the larger current to the point where the resultant magnetic field is zero?
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View SolutionTwo long straight parallel conductors 10 cm apart, carry currents of 5A each in the same direction. Then the magnetic induction at a point midway between them is
View SolutionWhen two wires have current in same direction then force is
View SolutionTwo long parallel straight wires X and Y separated by a distance 5cm in air carry currents of 10A and 5A respectively in opposite directions. Calculate the magnitude and direction of force on a 20cm length of the wire Y. Figure
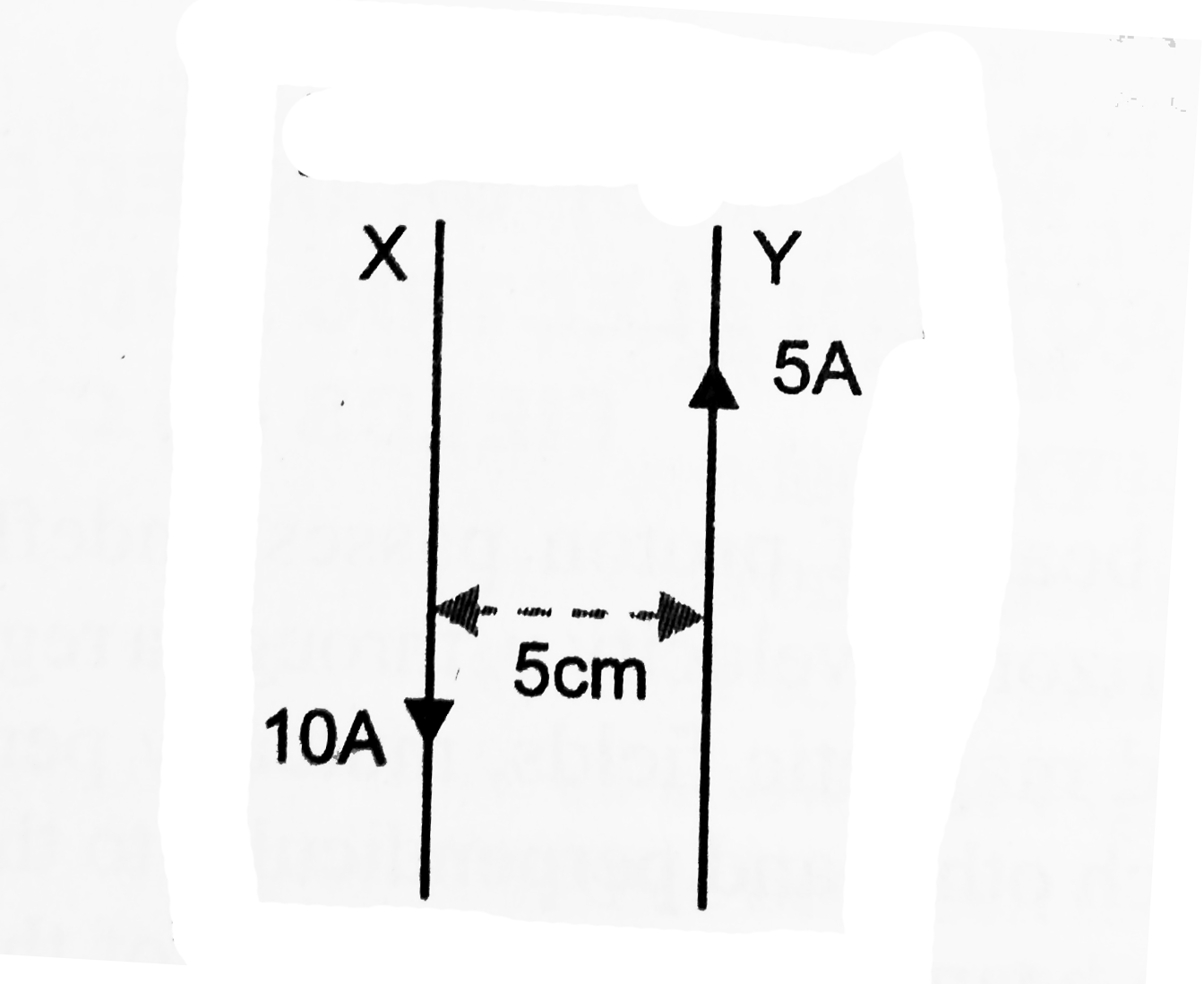
View Solution