Two long parallel wires placed 0.08 m apart, carry currents 3 A and 5 A in the same direction. what is the distance from the conductor carrying the larger current to the point where the resultant magnetic field is zero?
0.5 m
0.04 m
0.05 m
0.4m
The correct Answer is:C
To solve the problem step by step, we need to find the distance from the wire carrying the larger current (5 A) to the point where the resultant magnetic field is zero.
Step 1: Understand the setup
We have two long parallel wires, one carrying a current of 3 A and the other carrying a current of 5 A. The distance between the two wires is 0.08 m (or 8 cm). We need to find the distance from the wire carrying 5 A to the point where the magnetic fields due to both wires cancel each other out.
Step 2: Define the variables
Let:
- x = distance from the wire carrying 5 A to the point where the magnetic field is zero.
- The distance from the wire carrying 3 A to this point will then be 0.08−x.
Step 3: Write the formula for the magnetic field
The magnetic field B due to a long straight wire at a distance r is given by the formula:
B=μ0I2πr
where:
- μ0 = permeability of free space (a constant),
- I = current in the wire,
- r = distance from the wire.
Step 4: Calculate the magnetic fields
1. Magnetic field due to the 3 A wire (B1):
B1=μ0⋅32π(0.08−x)
This field is directed into the plane.
2. Magnetic field due to the 5 A wire (B2):
B2=μ0⋅52πx
This field is directed out of the plane.
Step 5: Set the magnetic fields equal for cancellation
For the resultant magnetic field to be zero, the magnitudes of B1 and B2 must be equal:
B1=B2
Substituting the expressions we derived:
μ0⋅32π(0.08−x)=μ0⋅52πx
The μ0 and 2π cancel out:
30.08−x=5x
Step 6: Cross-multiply to solve for x
Cross-multiplying gives:
3x=5(0.08−x)
Expanding the right side:
3x=0.4−5x
Combining like terms:
3x+5x=0.4
8x=0.4
x=0.48=0.05 m
Step 7: Conclusion
The distance from the wire carrying the larger current (5 A) to the point where the resultant magnetic field is zero is 0.05 m.
We have two long parallel wires, one carrying a current of 3 A and the other carrying a current of 5 A. The distance between the two wires is 0.08 m (or 8 cm). We need to find the distance from the wire carrying 5 A to the point where the magnetic fields due to both wires cancel each other out.
Let:
- x = distance from the wire carrying 5 A to the point where the magnetic field is zero.
- The distance from the wire carrying 3 A to this point will then be 0.08−x.
The magnetic field B due to a long straight wire at a distance r is given by the formula:
B=μ0I2πr
where:
- μ0 = permeability of free space (a constant),
- I = current in the wire,
- r = distance from the wire.
1. Magnetic field due to the 3 A wire (B1):
B1=μ0⋅32π(0.08−x)
This field is directed into the plane.
B2=μ0⋅52πx
This field is directed out of the plane.
For the resultant magnetic field to be zero, the magnitudes of B1 and B2 must be equal:
B1=B2
Substituting the expressions we derived:
μ0⋅32π(0.08−x)=μ0⋅52πx
The μ0 and 2π cancel out:
30.08−x=5x
Cross-multiplying gives:
3x=5(0.08−x)
Expanding the right side:
3x=0.4−5x
Combining like terms:
3x+5x=0.4
8x=0.4
x=0.48=0.05 m
The distance from the wire carrying the larger current (5 A) to the point where the resultant magnetic field is zero is 0.05 m.
Similar Questions
Knowledge Check
Two parallel wires 2 m apart carry currents of 2 A and 5 A respectively in same direction, the force per unit length acting between these two wires is
A2×10−6Nm−1B3×10−6Nm−1C1×10−6Nm−1D4×10−6Nm−1
Two long parallel wires are 30 cm apart carrying currents 10 A and 15 A respectively in the same direction. The force acting over a length of 5 m of the wires is
View SolutionTwo parallel wires P and Q placed at a separation
d=6cm carry electric currents i_1= 5A and i_2= 2A in <br> opposite directions as shown in figure. Find the<br> point on the line PQ where the resultant magnetic field
is zero.

View SolutionTwo long straight parallel conductors 10 cm apart, carry currents of 5A each in the same direction. Then the magnetic induction at a point midway between them is
View SolutionTwo long and parallel straight wires A and B carrying currents of 8⋅0A and 5⋅0A in the same direction are separated by a distance of 4⋅0cm. Estimate the force on a 10cm section of wire A.
View SolutionLet two long parallel wires, a distance d apart, carry equal currents I in the same direction. One wires at x=0, the other at x=d (as shown in Fig) Determine magnetic field at any point x-axis between the wires as a function of x.

View SolutionTwo infinitely long current carrying conductors X and Y are kept parallel to each other, 24 cm apart in vacuum. They carry currents of 5 A and 7 A respectively, in the same direction, as shown in figure bleow. Find the position of a neutral point, i.e., a point where
resultant magnetic flux density is zero. ( lgnore earth's magnetic field ).
View SolutionTwo infinitely long current carrying conductors X and Y are kept parallel to each other, 24 cm apart in vacuum. They carry currents of 5 A and 7 A respectively, in the same direction, as shown in figure below. Find the position of a neutral point, i.e., a point where resultant magnetic flux density is zero. (Ignore earth.s magnetic field).
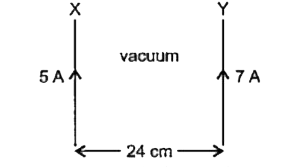
View Solution
