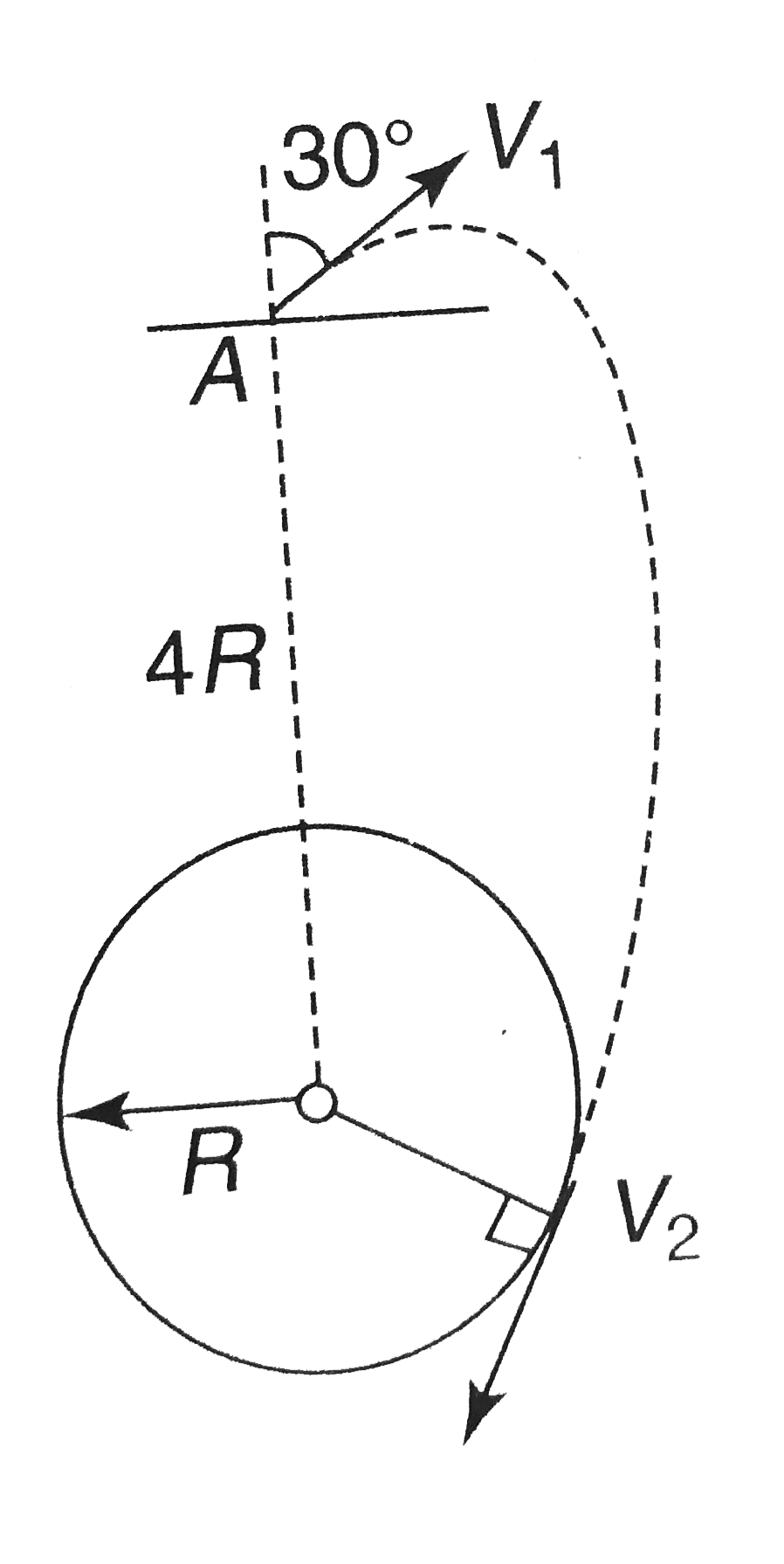
A particle is projected from point A, that is at a distance 4R form the centre of the earth, with speed V1 in a direction making 30∘ with the line joining the centre of the earth and point A, as shown. Consider gravitational interaction only between these two. (Use GMR=6.4×107m2/s2). The speed V1 if particle pasess grazing the surface of the earth is
4√2km s−1
3√2km s−1
6√2km s−1
5√2km s−1
The correct Answer is:A
Step by step video & image solution for A particle is projected from point A, that is at a distance 4R form the centre of the earth, with speed V_(1) in a direction making 30^(@) with the line joining the centre of the earth and point A, as shown. Consider gravitational interaction only between these two. (Use (GM)/R=6.4xx10^(7) m^(2)//s^(2)). The speed V_(1) if particle pasess grazing the surface of the earth is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
View SolutionA particle is projected vertically with speed V from the surface of the earth . Maximum height attained by the particle , in term of the radius of earth R,V and g is ( V < escape velocity , g is the acceleration due to gravity on the surface of the earth )
View Solution
Knowledge Check
The gravitational field intensity at a point 10,000km from the centre of the earth is 4.8Nkg−1. The gravitational potential at that point is
A−4.8×107Jkg−1B−2.4×107Jkg−1C4.8×106Jkg−1D3.6×106Jkg−1
If d is the distance between the centre of the earth of mass M1 and the moon of mass M2, then the velocity with which a body should be projected from the mid point of the line joining the earth and the moon, so that it just escape is
View SolutionIt takes time 8 min for light to reach from the sun to the earth surface. If speed of light is taken to be 3×108 m s−1, find the distance from the sun to the earth in km.
View SolutionTwo satellites S1 and S2 revolve around the earth at distances 3R and 6R from the centre of the earth. Find the ratio of their (a) linear speeds and (b) angular speeds.
View SolutionTwo particles of equal mass 'm' are projected from the ground with speed v1 and v2 at angles θ1 and θ2 at the same times as shown in figure. The centre of mass of the two particles.

View SolutionThe minimum and maximum distance of a satellite from the centre of the earth are 2R and 4R respectively, where R is the radius of earth and M is the mass of the earth. The radius of curvature at the point of maximum distance is
View SolutionA particle is projected vertically upward with with velocity √23GMR from the surface of Earth. The height attained by it is (G, M, R have usual meanings)
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View Solution
