Two slits and illuminated by a white light source give a white central maxima. A transparent sheet of refractive index 1.25 and thickness is placed in front of . Another transparent sheet of refractive index 1.50 and thickness is placed in front of . If central maxima is not effected, then ratio of the thickness of the two sheets will be :
The correct Answer is:B
To solve the problem, we need to find the ratio of the thickness of two transparent sheets placed in front of two slits, such that the central maxima remains unaffected.
1. Understanding Optical Path Length:
The optical path length (OPL) is given by the product of the refractive index (μ) of the medium and the actual path length (t). The formula for optical path length is:
OPL=μ×t
2. Identifying the Given Values:
- For the first slit S1:
- Refractive index μ1=1.25
- Thickness t1
- For the second slit S2:
- Refractive index μ2=1.50
- Thickness t2
3. Calculating the Optical Path Lengths:
- The optical path length for the first sheet in front of S1:
OPL1=μ1×t1=1.25t1
- The optical path length for the second sheet in front of S2:
OPL2=μ2×t2=1.50t2
4. Condition for Central Maxima:
For the central maxima to remain unaffected, the optical path lengths must be equal:
OPL1=OPL2
Therefore, we have:
1.25t1=1.50t2
5. Rearranging the Equation:
To find the ratio of the thicknesses t1t2:
t1t2=1.501.25
6. Simplifying the Ratio:
t1t2=1.50÷1.251.25÷1.25=1.50÷1.251=1.501.25=65=1210=21
7. Final Result:
The ratio of the thickness of the two sheets is:
t1t2=2:1
Conclusion:
Thus, the ratio of the thickness of the two sheets t1 and t2 is 2:1.
The optical path length (OPL) is given by the product of the refractive index (μ) of the medium and the actual path length (t). The formula for optical path length is:
OPL=μ×t
- For the first slit S1:
- Refractive index μ1=1.25
- Thickness t1
- For the second slit S2:
- Refractive index μ2=1.50
- Thickness t2
- The optical path length for the first sheet in front of S1:
OPL1=μ1×t1=1.25t1
- The optical path length for the second sheet in front of S2:
OPL2=μ2×t2=1.50t2
For the central maxima to remain unaffected, the optical path lengths must be equal:
OPL1=OPL2
Therefore, we have:
1.25t1=1.50t2
To find the ratio of the thicknesses t1t2:
t1t2=1.501.25
t1t2=1.50÷1.251.25÷1.25=1.50÷1.251=1.501.25=65=1210=21
The ratio of the thickness of the two sheets is:
t1t2=2:1
Thus, the ratio of the thickness of the two sheets t1 and t2 is 2:1.
Similar Questions
Find Brewster.s angle for a transparent liquid having refractive index 1.5.
View SolutionIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
View SolutionTo make the central fringe at the centerO , mica sheet of refractive index 1.5 is introduced Choose the corect statement.
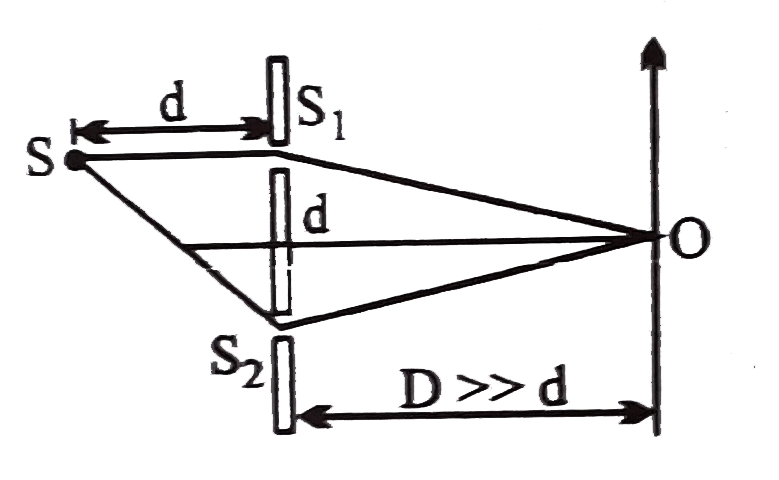
View SolutionYoung's double slit experiment is conducted in a liquid of refractive index μ1 as shown in figure. A thin transparent slab of refractive index μ2 is placed in front of the slit s2. The magnitude of optical path difference at 'O' is
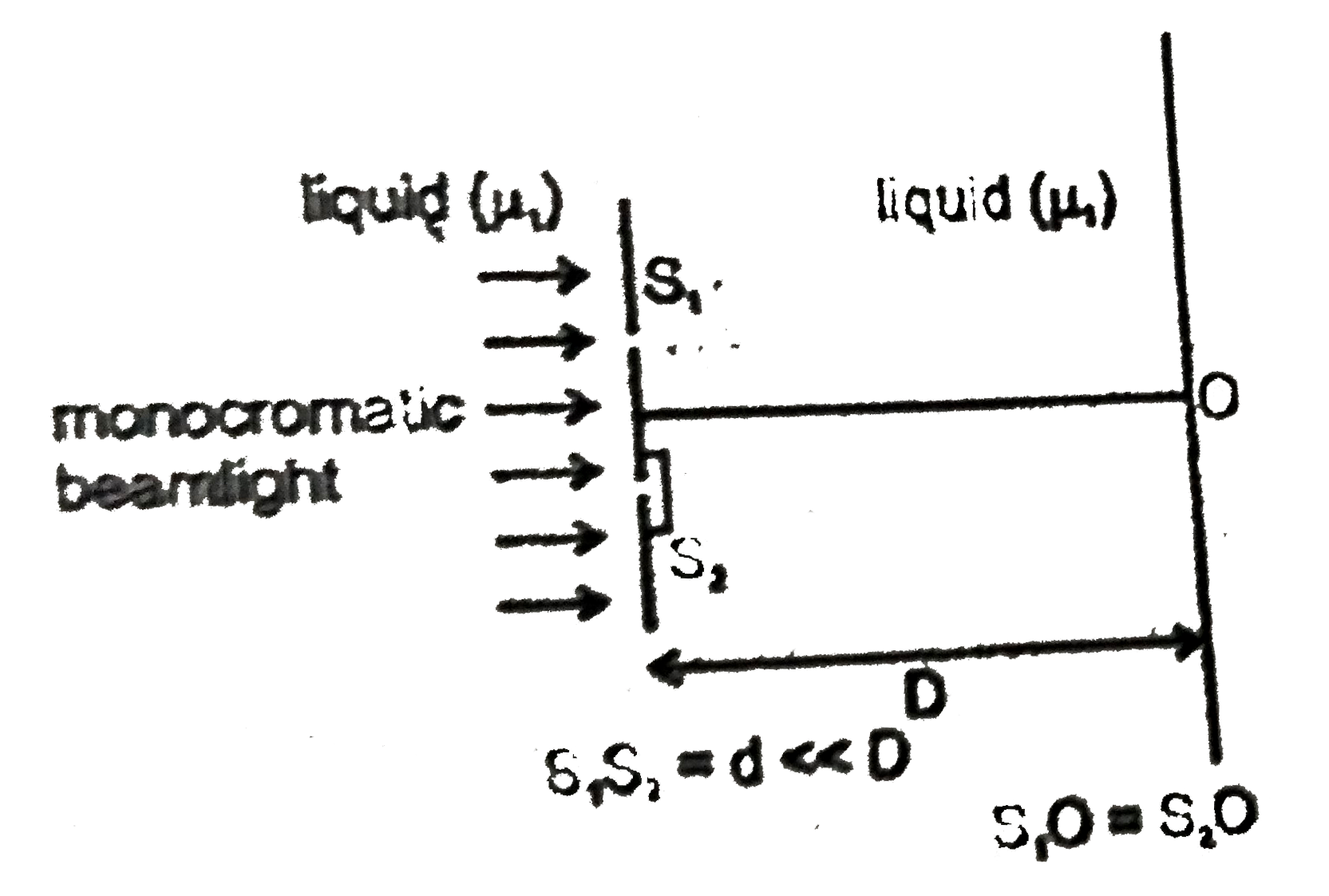
View SolutionPhase difference at the central point changes by π/3 when as thick film having a refractive index 1.5 and thickness 0.4μm is placed in front of upper slit of a YDSE set up. If the wavelength (in nm) of the light used is 600 k, find k.
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S1and S2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S1 and S2 medium of refractive index n1=2 is present and to the right of S1 and S2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.

In order to get central maxima at the centre of screen, the thickness of slab required is :
View SolutionIn figure S is a monochromatic source of light emitting light of wavelength of wavelength λ (in air). Light on slits S1 from S and then reaches in the slit S2 and S3 through a medium of refractive index μ1. Light from slit S2 and S3 reaches the screen through a medium of refractive index μ3. A thin transparent film of refractive index μ2 and thickness t is used placed in front of S2. Point P is symmetrical w.r.t. S2 and S3. Using the values d=1mm,D=1m,μ1=4/3,
μ2=3/2,μ3=9/5, and t=49×10−5m,
a. find distance of central maxima from P,
b. If the film in front of S2 is removed, then by what distance and in which direction will be central maxima shift ?
 .
.
View Solution_S01_025_Q01.png)
In Young's double slit experiment the slits, S1&S2 are illuminated by a parallel beam of light of wavelength 4000 Å from the medium of refractive index n1=1.2 A thin film of thickness 1.2 μm and refractive index n=1.5 is placed infrom of S1 perpedicular to path of light. the refractive index of medium between plane of slits & screen is n2=1.4 if the light coming from the film and S1&S2 have equal intensities I then intensity at geometrical centre of the screen O is
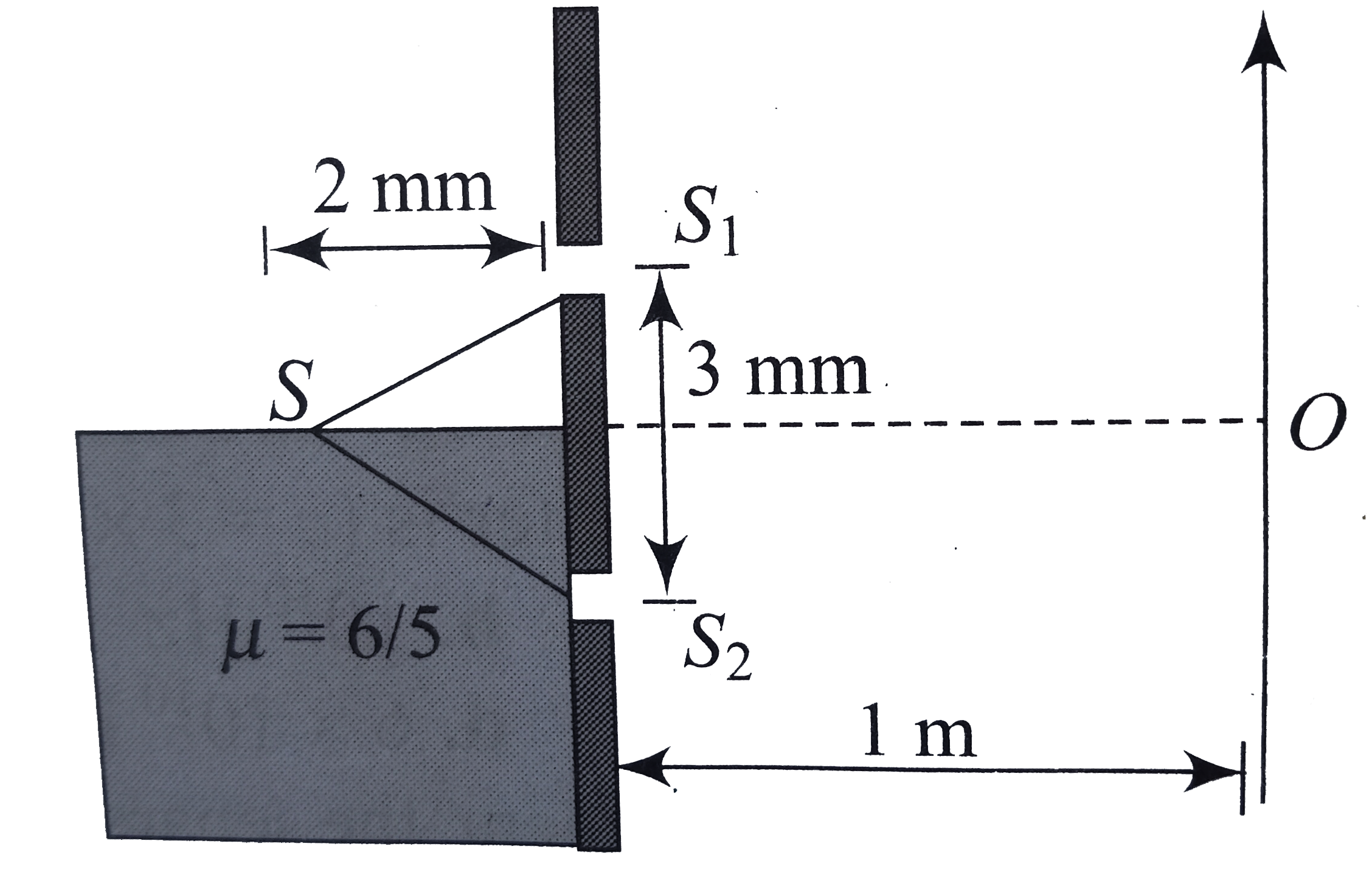
View SolutionIn Young's double-slit experiment, a point source is placed on a solid slab of refractive index 6/5 at a distance of 2 mm from two slits spaced 3 mm apart as shown and at equal distacne from both the slits. The screen is at a distance of 1 m from the slits. Wavelength of light used is 500 nm.
a. Find the position of the central maximum.
b. Find the order of the fringe formed at O.
c. A film of refractive index 1.8 is to be placed in front of S1 so that central maxima is formed where 200th maxima was formed. Find the thickness of film.
View SolutionIn YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
View Solution
