In YDSE arangement shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000∘Δ (in air). S1 and S2 are two slits separate by d=1mm and D=1m . Left of slits S1andS2 medium of refractive index μ1=2 is presernt refractive index μ2=32 is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of slab μ3 varies with distance from its starting face as shown in figure.

If the thickness of the slab is selected 1μm , then the position of the central maxima will be (y - coordinate)
13mm
−13mm
16mm
−16mm
The correct Answer is:C

Area (A)=μ3(dx)=(1+3)t2=2t
From the above equation
O=1×10−6+32ydD−0.5t32×ydD=0.5t−1×10−6
=0.5×10−6−1×10−6=−0.5×10−6
y=−10−62×23×Dd=−10−6×13×1×10−3=−13×10−3
y=−13mm
Topper's Solved these Questions
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - I(H.W)
20 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - II(H.W)
19 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - V
37 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - NARAYNACHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)
19 Videos
Similar Questions
The displacements of two interfering light waves are y1=2sinωt and y2=5sin(ωt+π3) the resultant amptitude is
View SolutionIn Young's double slit experiment the intensity of light at a point on the screen where the path difference λ is K. The intensity of light at a point where the path difference is λ6 [λ is the wavelength of light used] is
View SolutionTwo beam of light having intensities I and 4I interfere to produce a fringe pattern on a screen. The phase difference between the beams is π2 at point A and π at point B. Then the difference between resultant intensities at A and B is : (2001,2M)
View SolutionAssertion : the following circuit represents 'OR' gate

Reason : for the above circuit Y=¯¯¯X=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯A+B+A+B
View SolutionIn figure S is a monochromatic source of light emitting light of wavelength of wavelength lambda (in air). Light on slits S_(1) from S and then reaches in the slit S_(2) and S_(3) through a medium of refractive index mu_(1) . Light from slit S_(2) and S_(3) reaches the screen through a medium of refractive index mu_(3) . A thin transparent film of refractive index mu_(2) and thickness t is used placed in front of S_(2) . Point P is symmetrical w.r.t. S_(2) and S_(3) . Using the values d = 1 mm, D = 1 m, mu_(1) = 4//3 , mu_(2) = 3//2, mu_(3) = 9//5 , and t = (4)/(9) xx 10^(-5) m , a. find distance of central maxima from P, b. If the film in front of S_(2) is removed, then by what distance and in which direction will be central maxima shift ? .
View SolutionIn a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
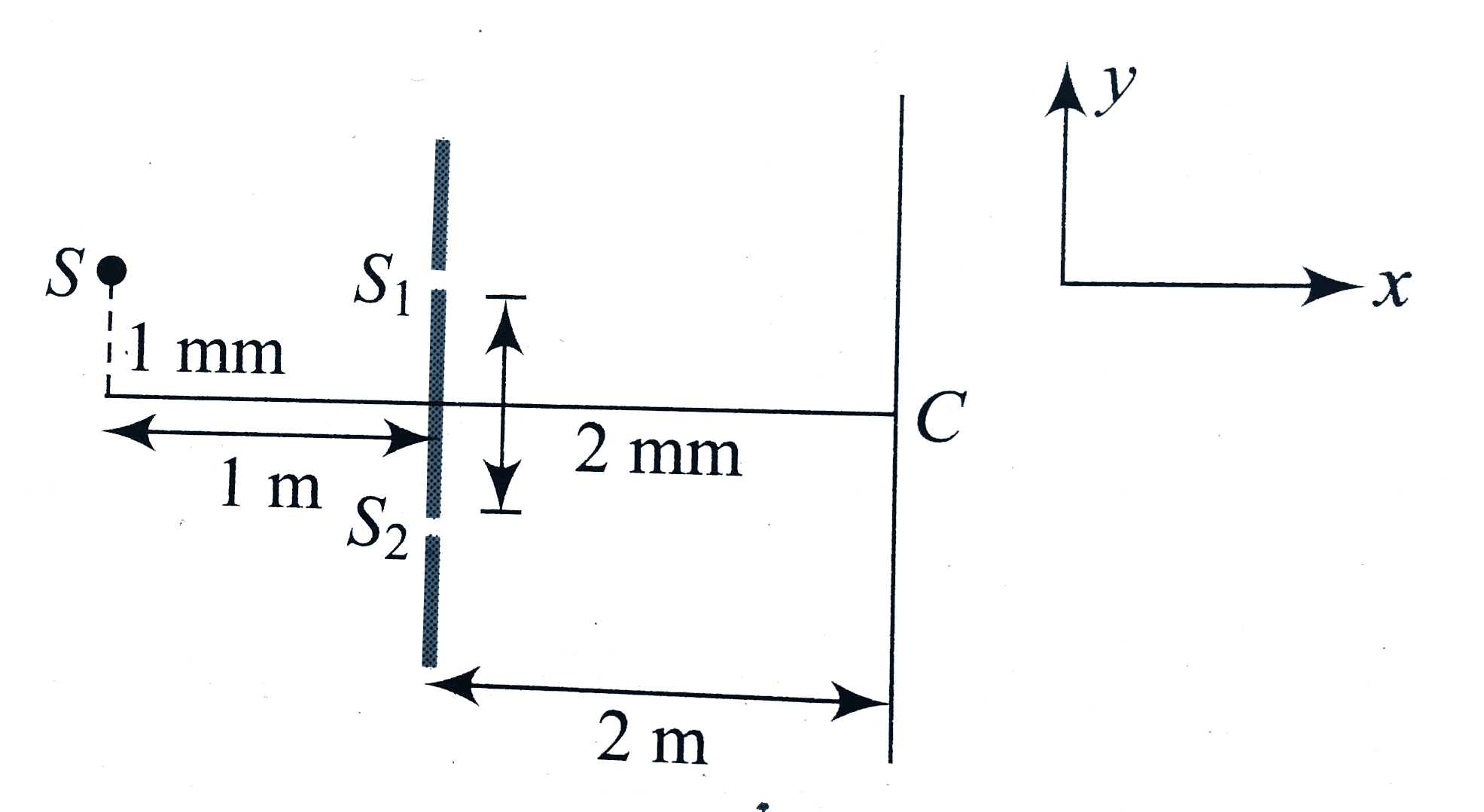
At t=1 s, a slab of thickness 2×10−3mm an refractive index 1.5 is placed just in front of S1. The central maximum is formed at
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S_1 and S_2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S_1 and S_2 medium of refractive index n_1 = 2 is present and to the right of S_1 and S_2 medium of n_2 = 3/2 , is present. A thin slab of thickness 't' is placed in front of S_1 . The refractive index of n_3 of the slab varies with distance from it's starting face as shown in figure. In order to get central maxima at the centre of screen, the thickness of slab required is :
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S_1 and S_2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S_1 and S_2 medium of refractive index n_1 = 2 is present and to the right of S_1 and S_2 medium of n_2 = 3/2 , is present. A thin slab of thickness 't' is placed in front of S_1 . The refractive index of n_3 of the slab varies with distance from it's starting face as shown in figure. If thickness of the slab is selected 1 mum , then position of central maxima will be : (y-coordinate)
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S_1 and S_2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S_1 and S_2 medium of refractive index n_1 = 2 is present and to the right of S_1 and S_2 medium of n_2 = 3/2 , is present. A thin slab of thickness 't' is placed in front of S_1 . The refractive index of n_3 of the slab varies with distance from it's starting face as shown in figure. Fringe width on the screen is
View SolutionIn a YDSE two him transparent sheet are used in front of the slits S_(1) & S_(2) having mu_(1)=1.6 and mu_(2)=1.4 respectively.If both sheets have thickness t ,the central maximum is observed at a distance of 5mm from center O .Now the sheets are replaced by another two sheets each of refractive index (mu_(1)-mu_(2))/(2) but having thickness t_(1)&t_(2)=(t_(1)-t_(2))/(2) .Now central maximum is observed at distance of 8mm from center O on the same side as before.Find the thickness t_(1) (in mu m) [Given:d=1mm,D=1m]
View Solution_S01_025_Q01.png)
In Young's double slit experiment the slits, S1&S2 are illuminated by a parallel beam of light of wavelength 4000 Å from the medium of refractive index n1=1.2 A thin film of thickness 1.2 μm and refractive index n=1.5 is placed infrom of S1 perpedicular to path of light. the refractive index of medium between plane of slits & screen is n2=1.4 if the light coming from the film and S1&S2 have equal intensities I then intensity at geometrical centre of the screen O is
View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
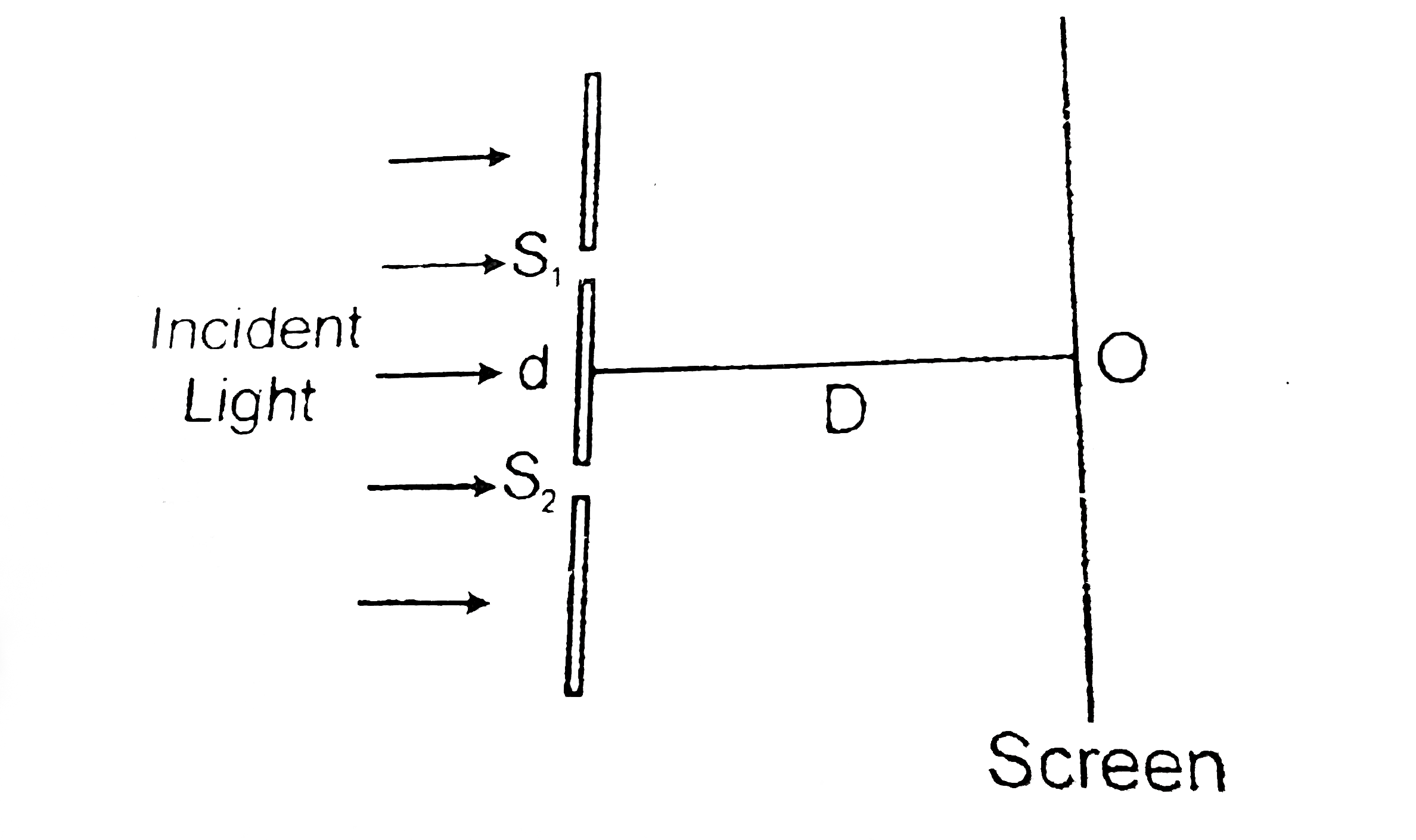
Due to placement of film in front of S1, how many bright fringes cross the point O of screen excluding the one which was at O earlier :
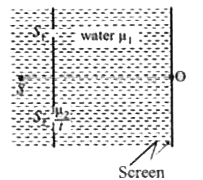
View SolutionA YDSE is conducted in water (μ1) as shown in figure. A glass plate of thickness t and refractive index μ2 is placed in the path of S2. The optical path difference at O is
View SolutionIn Young's double slit experiment S1 and S2 are two slits. Films of thickness t1 and t2 and refractive indices μ1 and μ2 are placed in front of S1 and S2 respectively. If μ1t1=μ2t2, then the central maximum will :
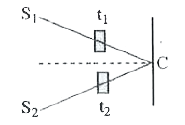
View SolutionIn Young.s double slit experiment S1 andS2 are two slits. Films of thicknesses t1 and t2 refractive indices μ1andμ2 are placed in front ofS1andS2 repectively. If μ1t1=μ2t2 , then the central maximum will
View Solution
