A cord of length 64m is used to connected a 100kg astronaut to spaceship whose mass is much larger than that of the astronuat. Estimate the value of the tension in the cord. Assume that the spaceship is orbiting near earth surface. Assume that the spaceship and the astronaut fall on a straight line from the earth centre. the radius of the earth is 6400km.
3×10−2N
2×10−2N
4×10−2N
5×10−2N
The correct Answer is:A
To solve the problem of finding the tension in the cord connecting the astronaut to the spaceship, we can follow these steps:
Step 1: Identify the Forces Acting on the Astronaut
The astronaut experiences two main forces:
1. The gravitational force (Fg) acting downwards towards the Earth.
2. The tension (T) in the cord acting upwards towards the spaceship.
Step 2: Write the Equation for Centripetal Force
Since the astronaut is in orbit, the net force acting on him must provide the necessary centripetal force (Fc). The equation can be written as:
T−Fg=Fc
Where:
- Fg=GMEm(R+L)2 (gravitational force)
- Fc=m(R+L)ω2 (centripetal force)
Step 3: Calculate Angular Velocity (ω)
The angular velocity (ω) can be derived from the gravitational force acting on the spaceship:
GMEmR2=mRω2
From this, we can isolate ω:
ω=√GMER3
Step 4: Substitute ω into the Centripetal Force Equation
Substituting ω back into the centripetal force equation:
Fc=m(R+L)(√GMER3)2
This simplifies to:
Fc=m(R+L)GMER3
Step 5: Substitute Fg and Fc into the Tension Equation
Now we can substitute Fg and Fc into the tension equation:
T=Fc+Fg
Substituting the expressions we derived:
T=m(R+L)GMER3+GMEm(R+L)2
Step 6: Simplify the Equation
To simplify, we can factor out GMEm:
T=GMEm((R+L)R3+1(R+L)2)
Step 7: Substitute Known Values
Given:
- Mass of astronaut m=100kg
- Length of the cord L=64m
- Radius of the Earth R=6400km=6400×103m
- Gravitational constant G=6.674×10−11m3/kg s2
- Mass of Earth ME≈5.972×1024kg
Step 8: Calculate the Tension
Now we can plug in the values into the simplified tension equation to find T.
Final Calculation
After performing the calculations, we find:
T≈3×10−2N
Conclusion
The estimated value of the tension in the cord is approximately 0.03N.
---
The astronaut experiences two main forces:
1. The gravitational force (Fg) acting downwards towards the Earth.
2. The tension (T) in the cord acting upwards towards the spaceship.
Since the astronaut is in orbit, the net force acting on him must provide the necessary centripetal force (Fc). The equation can be written as:
T−Fg=Fc
Where:
- Fg=GMEm(R+L)2 (gravitational force)
- Fc=m(R+L)ω2 (centripetal force)
The angular velocity (ω) can be derived from the gravitational force acting on the spaceship:
GMEmR2=mRω2
From this, we can isolate ω:
ω=√GMER3
Substituting ω back into the centripetal force equation:
Fc=m(R+L)(√GMER3)2
This simplifies to:
Fc=m(R+L)GMER3
Now we can substitute Fg and Fc into the tension equation:
T=Fc+Fg
Substituting the expressions we derived:
T=m(R+L)GMER3+GMEm(R+L)2
To simplify, we can factor out GMEm:
T=GMEm((R+L)R3+1(R+L)2)
Given:
- Mass of astronaut m=100kg
- Length of the cord L=64m
- Radius of the Earth R=6400km=6400×103m
- Gravitational constant G=6.674×10−11m3/kg s2
- Mass of Earth ME≈5.972×1024kg
Now we can plug in the values into the simplified tension equation to find T.
After performing the calculations, we find:
T≈3×10−2N
The estimated value of the tension in the cord is approximately 0.03N.
Similar Questions
A particle is dropped down in a deep hole which extends to the centre of the earth. Calculate the velocity at a depth of one km from the surface of this carth ? Assume that g=10m/s2 and radius of the earth = 6400 km.
View SolutionAn astronaut orbiting in a spaceship round the earth, has centripetal acceleration 2.45m/s2. Find the height of the spaceship. (Take R = 6400 km).
View SolutionAn astronaut of mass m is working on a satellite orbiting the earth at a distance h from the earth's surface the radius of the earth is R while its mass is M the gravitational pull FG on the astronaut is
View SolutionA spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?
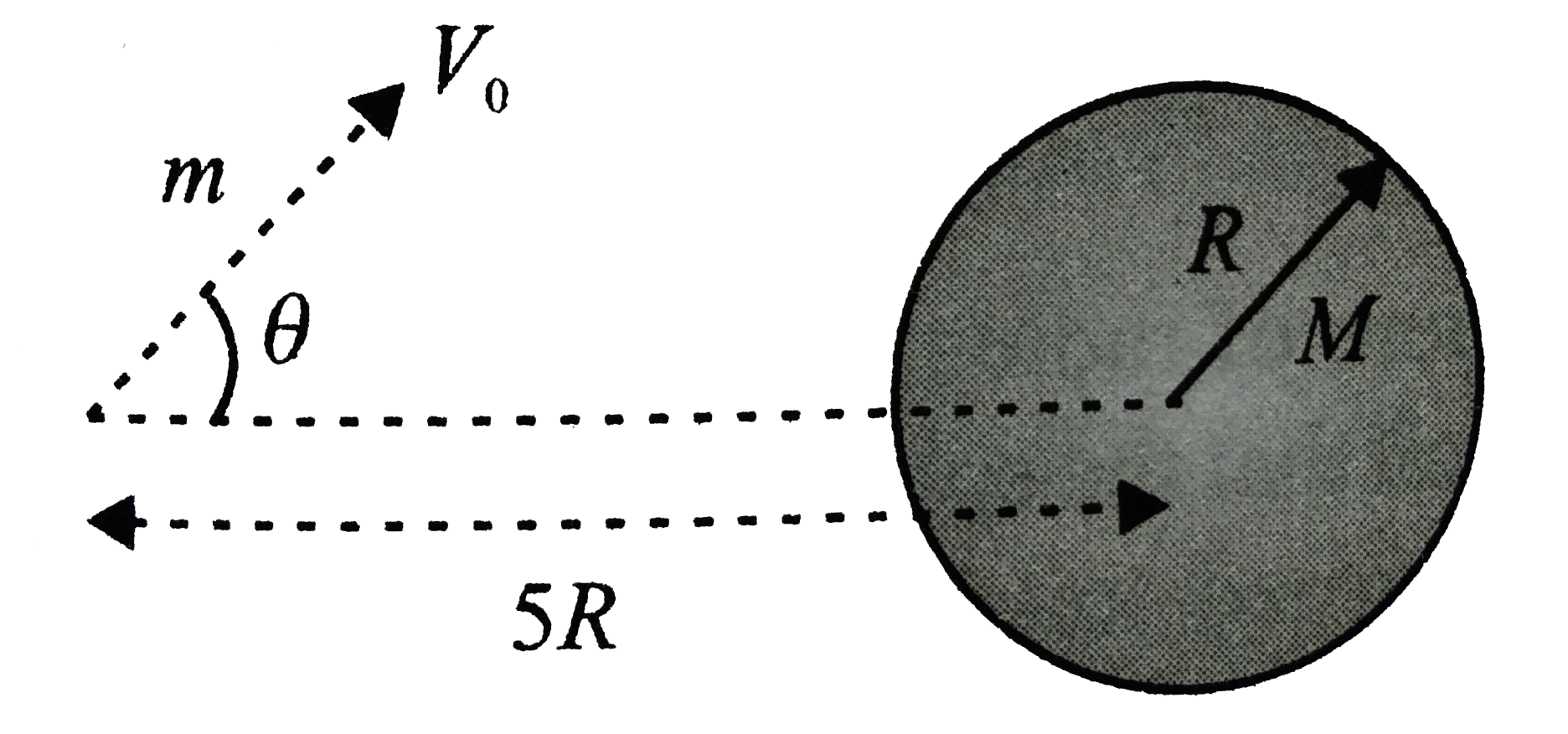
View SolutionA spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?

View SolutionA satellite is to be put into an orbit 600km above the surface of the earth. If its vertical velocity after launching is 2400m/s at this height, calculate the magnitude and direction in the impulse required to put the satellite directly increase. The mass of the satellite is 60kg and the radius of the earth is 6400km. Take g=10ms−2
View SolutionA spaceship is launched into a circular orbit close to the earth's surface . What additional velocity has now to be imparted to the spaceship in the orbit to overcome the gravitational pull. Radius of earth =6400km, g=9.8m/s2.
View SolutionA space klship is launched into a circular orbit close earth's surface. What additional velocity has now to imparted to the spaceship in the orbit to overcome gravitational pull?
(Radius of earth =6400 km,g=9.8m/s2)
View SolutionA space-ship is launched into a circular orbit close to the Earth,s surface. What additional speed should now be imparted to the spaceship so that it overcome the gravitational pull of the Earth.
Take kinetic energy of the space-ship,
K = total energy of space-ship =GMm2R
where m = mass of space-ship, M= mass of the earth and R = radius of the earth.
View Solution(a) Assuming the earth to be a sphere of uniform density, calculate the value of acceleration due to gravity at a point (i) 1600km above the earth, (ii) 1600km below the earth, (b) Also find the rate of variation of acceleration due to gravity above and below the earth's surface. Radius of earth =6400km,g9.8m/s2.
View Solution
