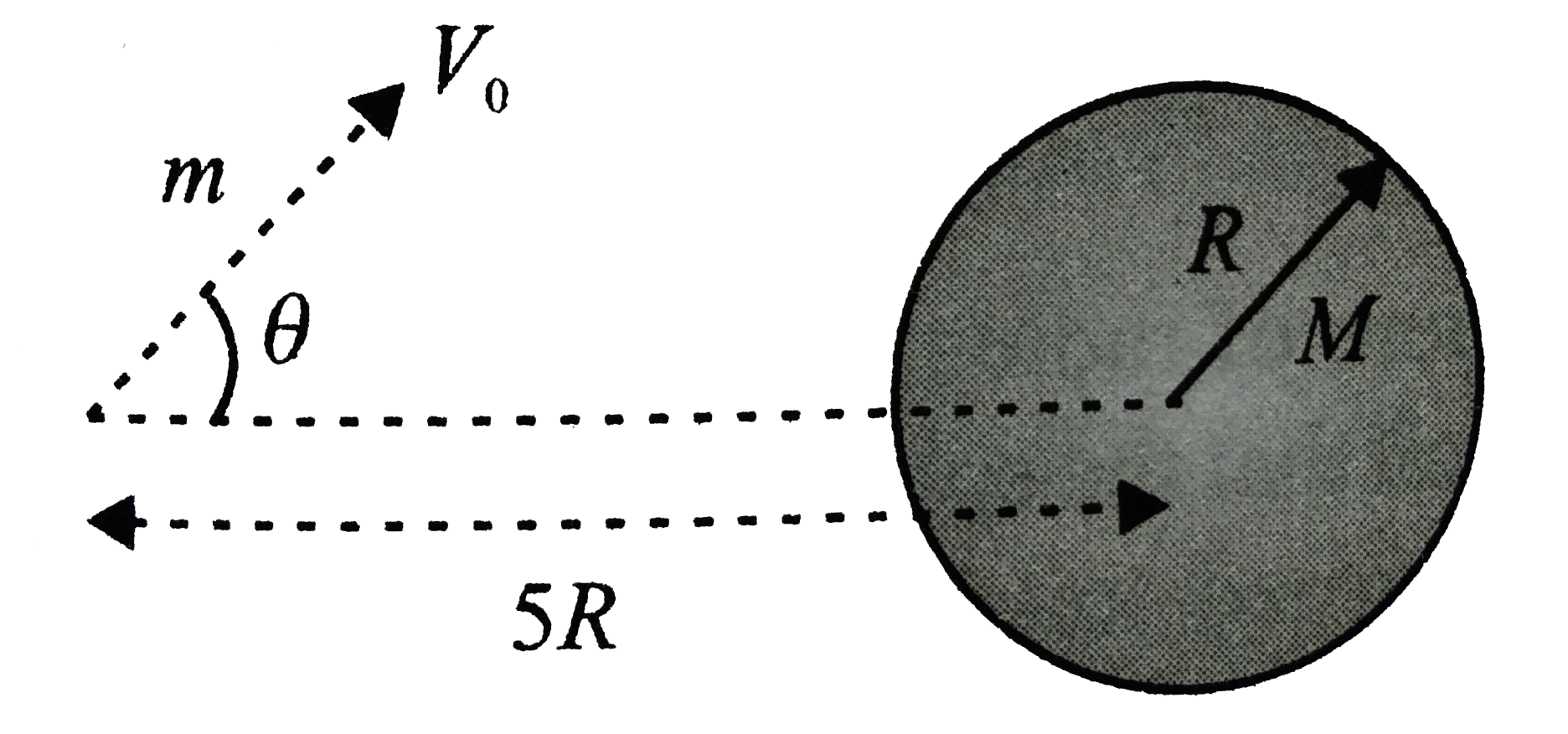
A spaceship is sent to investigate a planet of mass $M$ and radius $R$ . While hanging motionless in space at a distance $5 R$ from the centre of the planet, the spaceship fires an instrument package of mass $m$ , which is much smaller than the mass of the spaceship. For what angle $θ$ will the package just graze the surface of the planet?

Video Solution

Text Solution

Verified by Experts

The correct Answer is: ${sin}^{- 1} (\frac{1}{5} \sqrt{1 + \frac{8 G M}{5} v_{0}^{2} R}))$

Let the speed of the instrument package be $v$ when it grazes the surface of the planet.

Conserving angular momentum of the package about the centre of the planet
$m v_{0} \times 5 R sin t η = m v R$
$\Rightarrow v = 5 v_{0} sin θ$
Conserving mechanical energy, we get ...........i
$- \frac{G M m}{5 R} + \frac{1}{2} m v_{0}^{2} = - \frac{G M m}{R} + \frac{1}{w} m v^{2}$
$\Rightarrow \frac{1}{2} m (v^{2} - v_{0}^{2}) = \frac{4 G M m}{5 R}$
$\Rightarrow v^{2} = v_{0}^{2} = \frac{8 G M}{5 R}$ ..............ii
Substituting the value of $v$ from eqn i in Eqn ii we have
$25 v_{0}^{2} sin θ - v_{0}^{2} = \frac{8 G M}{5 R}$
$\Rightarrow θ = {sin}^{- 1} ⎛ ⎝ \frac{1}{5} \sqrt{1 + \frac{8 G M}{5 v_{0}^{2} R}} ⎞ ⎠$

Updated on:21/07/2023

|

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

A mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass m is
A $\frac{G M m}{\sqrt{2} R^{2}}$
B $\frac{G M m}{2 R^{2}}$
C $\frac{G M m}{2 \sqrt{2} R^{2}}$
D $\frac{G M m}{4 R^{2}}$

CENGAGE PHYSICS ENGLISH-GRAVITATION-Subjective

Home
Ask Doubt
Profile