When 500 calories heat is given to the gas X in an isobaric process, its work done comes out as 142.8 calories . The gas X is
O2
NH3
He
SO2
The correct Answer is:A
To solve the problem step by step, we will analyze the information given and apply the relevant thermodynamic principles.
Step 1: Understand the Process
In an isobaric process (constant pressure), the heat added to the system (gas X) is related to the change in enthalpy (ΔH) and the work done (W) by the system.
Step 2: Identify the Given Values
- Heat added (Q) = 500 calories
- Work done (W) = 142.8 calories
Step 3: Apply the First Law of Thermodynamics
According to the first law of thermodynamics, the change in internal energy (ΔU) can be expressed as:
ΔU=Q−W
Substituting the values:
ΔU=500 calories−142.8 calories=357.2 calories
Step 4: Relate ΔH and ΔU
In an isobaric process, the relationship between enthalpy (ΔH) and internal energy (ΔU) is given by:
ΔH=ΔU+PΔV
Since we are at constant pressure, we can also express this in terms of heat capacities:
ΔH=nCpΔTandΔU=nCvΔT
Step 5: Find the Ratio of Heat Capacities
The ratio of the heat capacities can be expressed as:
CpCv=ΔHΔU
Substituting the values we calculated:
CpCv=500 calories357.2 calories≈1.4
Step 6: Determine the Type of Gas
The ratio CpCv is related to the degrees of freedom of the gas. For a diatomic gas, this ratio is typically 75=1.4. Thus, gas X is likely a diatomic gas.
Step 7: Identify the Gas
Among common diatomic gases, oxygen (O₂) is a well-known example. Therefore, the gas X is oxygen.
Final Answer
The gas X is Oxygen (O₂).
---
In an isobaric process (constant pressure), the heat added to the system (gas X) is related to the change in enthalpy (ΔH) and the work done (W) by the system.
- Heat added (Q) = 500 calories
- Work done (W) = 142.8 calories
According to the first law of thermodynamics, the change in internal energy (ΔU) can be expressed as:
ΔU=Q−W
Substituting the values:
ΔU=500 calories−142.8 calories=357.2 calories
In an isobaric process, the relationship between enthalpy (ΔH) and internal energy (ΔU) is given by:
ΔH=ΔU+PΔV
Since we are at constant pressure, we can also express this in terms of heat capacities:
ΔH=nCpΔTandΔU=nCvΔT
The ratio of the heat capacities can be expressed as:
CpCv=ΔHΔU
Substituting the values we calculated:
CpCv=500 calories357.2 calories≈1.4
The ratio CpCv is related to the degrees of freedom of the gas. For a diatomic gas, this ratio is typically 75=1.4. Thus, gas X is likely a diatomic gas.
Among common diatomic gases, oxygen (O₂) is a well-known example. Therefore, the gas X is oxygen.
The gas X is Oxygen (O₂).
Similar Questions
Knowledge Check
How much work can be done by 100 calories of heat?
A100 JB420 JC42 JD4200 J
In a isobaric process the work done by a di-atomic gas is 10 J , the heat given to the gas will be :
View SolutionHow much work can be done by 100 calories of heat?
View SolutionIn thermodynamic process, 200 Joules of heat is given to a gas and 100 Joules of work is also done on it. The change in internal energy of the gas is
View SolutionA sample of gas is going through cyclic process, work done by gas is
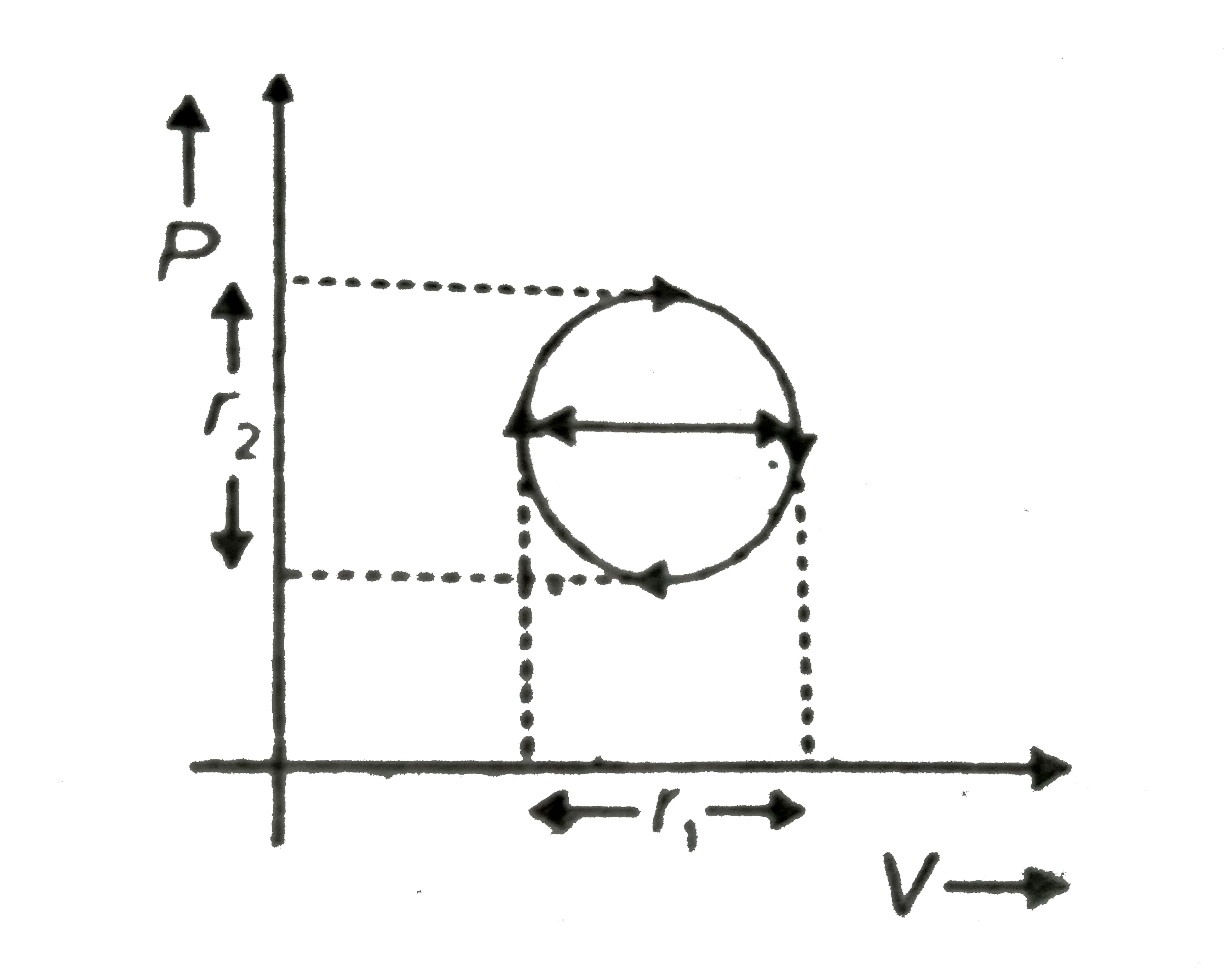
View SolutionWork done (in kJ) by the gas in the following cyclic process is
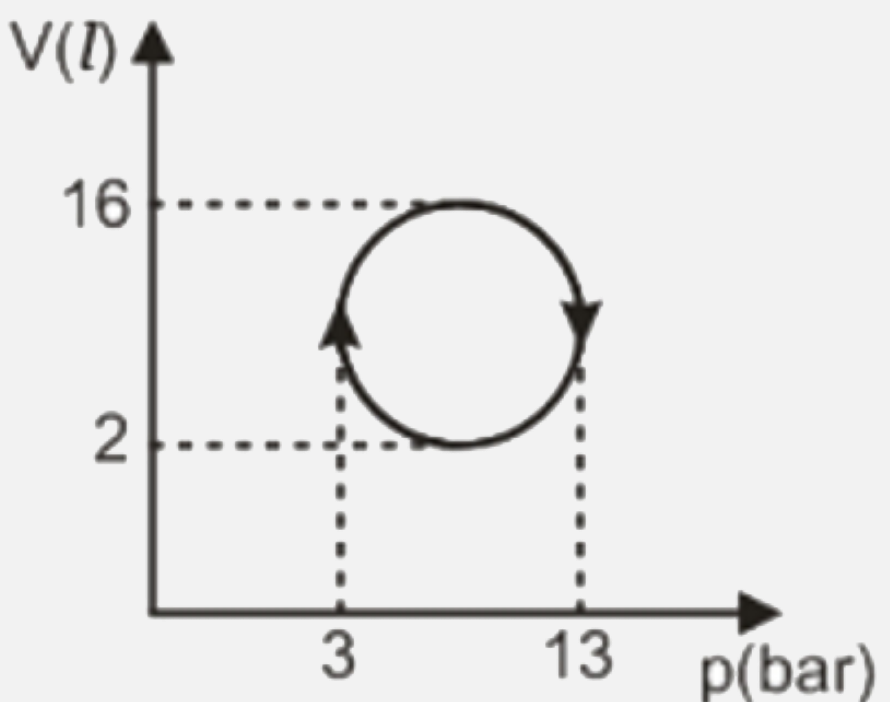
View SolutionThe thermodynamic process in which no work is done on or by the gas is
View SolutionTo raise the temperature of a certain mass of gas by 50∘C at a constant pressure , 160 calories of heat is required . When the sam mass of gas is cooled by 100∘C at constant volume 240 calories of heat is released . How many degrees of freedom does each molecule of this gas have (assume gas to be ideal) ?
View Solution
