In a isobaric process the work done by a di-atomic gas is 10 J , the heat given to the gas will be :
35 J
30 J
45 J
60 J
The correct Answer is:A
To solve the problem, we need to find the heat given to a diatomic gas during an isobaric process when the work done by the gas is 10 J.
1. Understand the Isobaric Process:
In an isobaric process, the pressure remains constant. The work done (W) by the gas can be expressed as:
W=n⋅R⋅T
where n is the number of moles, R is the universal gas constant, and T is the temperature.
2. Heat in an Isobaric Process:
The heat (Q) added to the gas at constant pressure is given by:
Q=n⋅Cp⋅ΔT
where Cp is the specific heat at constant pressure.
3. Relate Work Done and Heat:
From thermodynamic principles, we can relate the work done and heat added in an isobaric process:
WQ=RCp
Rearranging this gives us:
Q=W⋅CpR
4. Determine Cp for a Diatomic Gas:
For a diatomic gas, the degrees of freedom (f) is 5. The specific heat at constant pressure can be expressed as:
Cp=f+22R=5+22R=72R
5. Substituting Cp into the Heat Equation:
Substitute Cp into the equation for Q:
Q=W⋅(72R)R
The R cancels out:
Q=W⋅72
6. Calculate Heat (Q):
Given that W=10J:
Q=10⋅72=10⋅3.5=35J
Final Answer:
The heat given to the gas is Q=35J.
---
In an isobaric process, the pressure remains constant. The work done (W) by the gas can be expressed as:
W=n⋅R⋅T
where n is the number of moles, R is the universal gas constant, and T is the temperature.
The heat (Q) added to the gas at constant pressure is given by:
Q=n⋅Cp⋅ΔT
where Cp is the specific heat at constant pressure.
From thermodynamic principles, we can relate the work done and heat added in an isobaric process:
WQ=RCp
Rearranging this gives us:
Q=W⋅CpR
For a diatomic gas, the degrees of freedom (f) is 5. The specific heat at constant pressure can be expressed as:
Cp=f+22R=5+22R=72R
Substitute Cp into the equation for Q:
Q=W⋅(72R)R
The R cancels out:
Q=W⋅72
Given that W=10J:
Q=10⋅72=10⋅3.5=35J
The heat given to the gas is Q=35J.
Similar Questions
In isobaric process of ideal gas (f=5) work done by gas is equal of 10J. Then heat given to gas during process:
View SolutionDuring an isobaric heating process the work done by oxygen gas is 4 J. Calculate the amount of heat transferred to the gas. [γ=1.4]
View SolutionThe ratio of work done by an ideal diatomic gas to the heat supplied by the gas in an isobatic process is
View SolutionDuring an expansion of ideal gas the work done by gas is 100J and the heat capacity to process is found to be +2J/∘C. Find ΔE fo gas if the final temperature of gas is 25∘C higher than its initial temperature.
View SolutionStatement 1: Heat supplied to a gas is process is 100 J and work done by the gas in the same process is 120 J, then pressure of he gas in the process should increase.
because
Statement2: Work done by the gas is greater than the heat supplied to the gas. Hence, internal energy of the gas should decrease.
View SolutionIn an isobaric process, heat is supplied to a monoatomic ideal gas. The fraction of heat that goes itno mechanical work is
View SolutionThe work done by the gas in the process shown in given P-V diagram is
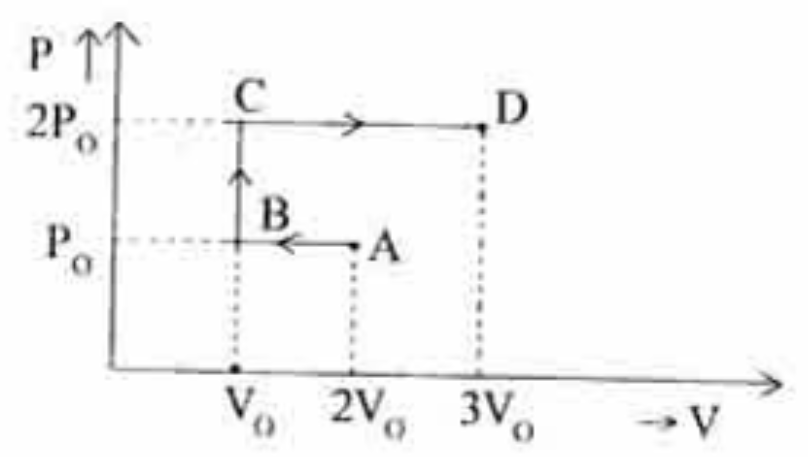
View SolutionAn ideal gas with adiabatic exponent (γ=1.5) undergoes a process in which work done by the gas is same as increase in internal energy of the gas. Here R is gas constant. The molar heat capacity C of gas for the process is:
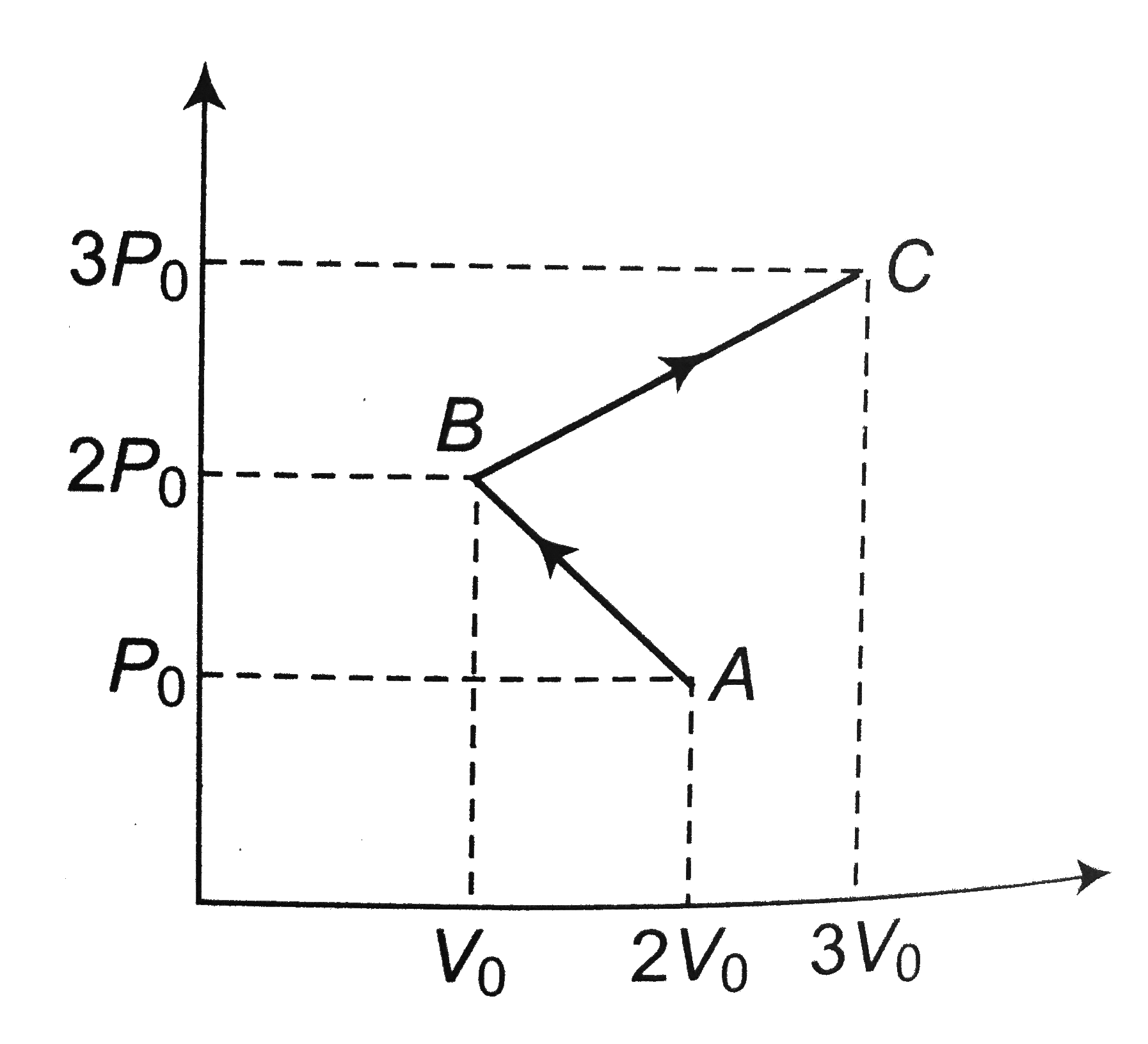
View SolutionFind the work done by the gas in the process ABC.
View SolutionIn a given process work done on a gas is 40 J and increase in its internal energy is 10J. Find heat given or taken to/from the gas in this process.
View Solution
