A block of mass 1 kg is connected with a smooth plank of the same mass is performing oscillations. The value of the spring constant is 200Nm−1 The block and the plank are free to move and there is no friction anywhere. The angular frequency of the oscillation is ω rad s−1 Find the value of ω
The correct Answer is:20
To find the angular frequency ω of the oscillating system consisting of a block and a plank, we can follow these steps:
Step 1: Identify the parameters
We have:
- Mass of the block, m=1kg
- Mass of the plank, m=1kg
- Spring constant, k=200N/m
Step 2: Understand the system
The system consists of two masses (the block and the plank) connected by a spring. Since there is no friction, both masses can move freely.
Step 3: Use the concept of reduced mass
For a system with two masses m1 and m2, the reduced mass μ is given by:
μ=m1⋅m2m1+m2
In our case, both masses are equal:
m1=m2=1kg
Thus, the reduced mass μ becomes:
μ=1⋅11+1=12kg=0.5kg
Step 4: Calculate the angular frequency ω
The angular frequency ω for a mass-spring system is given by:
ω=√kμ
Substituting the values of k and μ:
ω=√2000.5=√400
Step 5: Find the final value of ω
Calculating the square root:
ω=20rad/s
Conclusion
Thus, the angular frequency of the oscillation is:
ω=20rad/s
---
We have:
- Mass of the block, m=1kg
- Mass of the plank, m=1kg
- Spring constant, k=200N/m
The system consists of two masses (the block and the plank) connected by a spring. Since there is no friction, both masses can move freely.
For a system with two masses m1 and m2, the reduced mass μ is given by:
μ=m1⋅m2m1+m2
In our case, both masses are equal:
m1=m2=1kg
Thus, the reduced mass μ becomes:
μ=1⋅11+1=12kg=0.5kg
The angular frequency ω for a mass-spring system is given by:
ω=√kμ
Substituting the values of k and μ:
ω=√2000.5=√400
Calculating the square root:
ω=20rad/s
Thus, the angular frequency of the oscillation is:
ω=20rad/s
Similar Questions
A mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
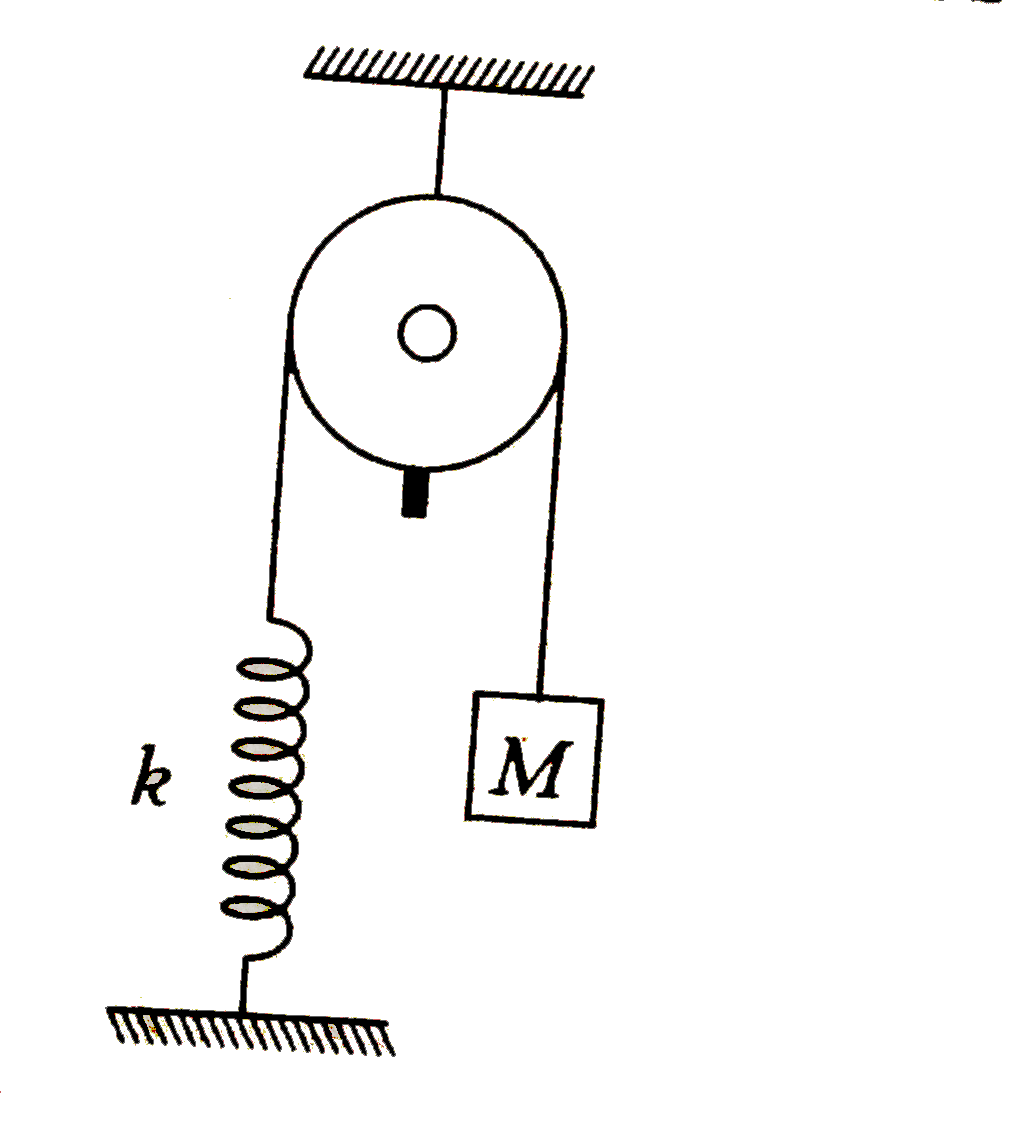 View Solution
View SolutionSpring of spring constant 1200Nm−1 is mounted on a smooth fricationless surface and attached to a block of mass 3kg. Block is pulled 2cm to the right and released. The angular frequency of oscillation is
_S01_037_Q01.png) View Solution
View SolutionA block of mass m is connected rigidly with a smooth wedge (plank) by a light spring of stiffness k. If the wedge is moved with constant velocity v0, find the work done by the external agent till the maximum compression of the spring.
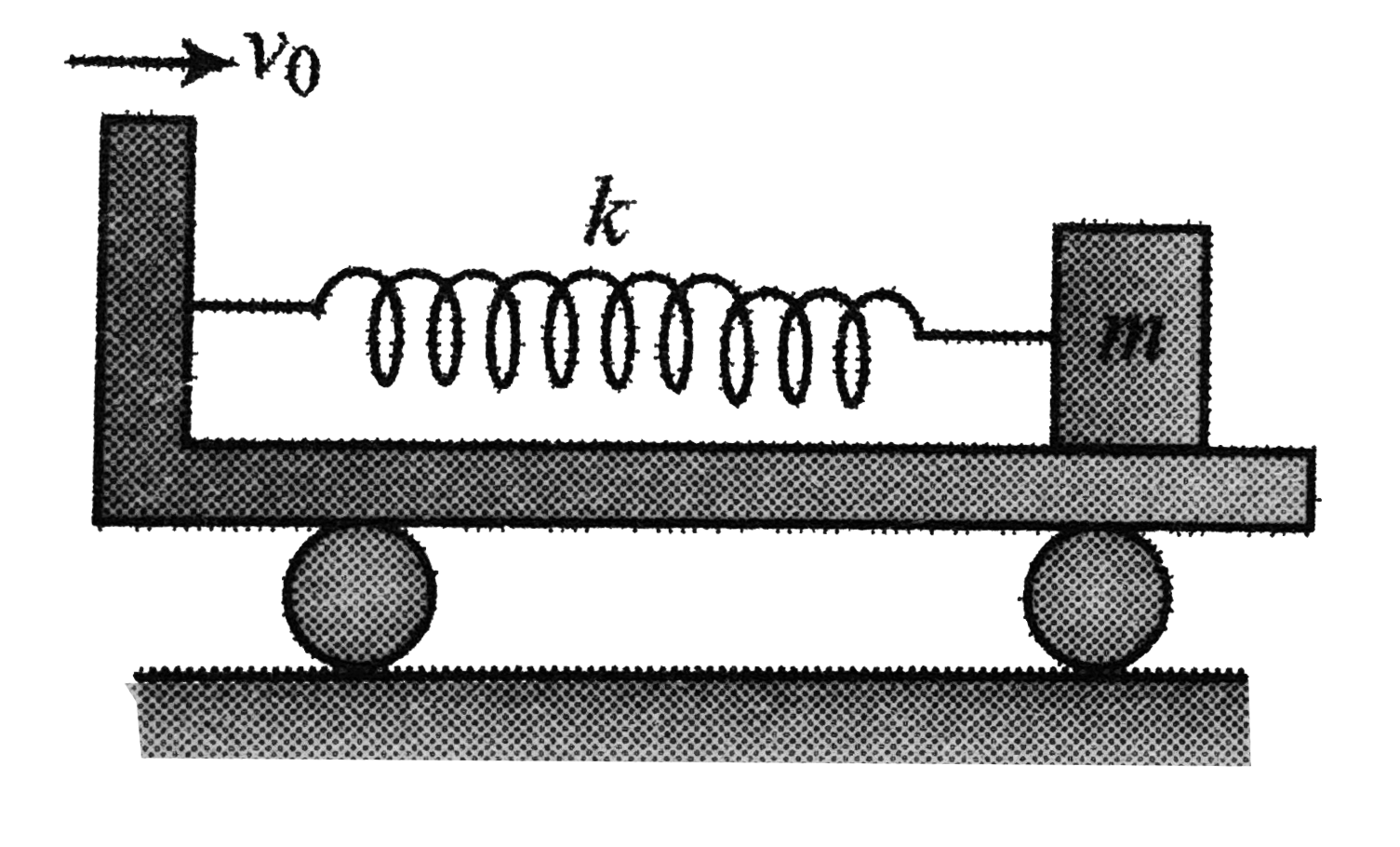 View Solution
View SolutionA block of mass m connected with a smooth prismatic wedge of mass M is released from rest when the spring is relaxed. Find the angular frequency of oscillation.
 View Solution
View SolutionA block of mass 0.01 kg is attached to a spring of force constant 10−1Nm−1 . If the energy of oscillation is 10−5 J, find the angular frequency and amplitude of oscillation.
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View SolutionA block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 View Solution
View SolutionA block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest
 View Solution
View SolutionA block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest
 View Solution
View Solution
