Question

An thin Plano - convex glass lens $(\mu =1.5)$ has its plane surface silvered and R is the radius of curvature of curved part, then which of the following ray diagram is true for an object placed at O ?
(O is at a distance of 2 R from the lens)

Options

A.
B.
C.
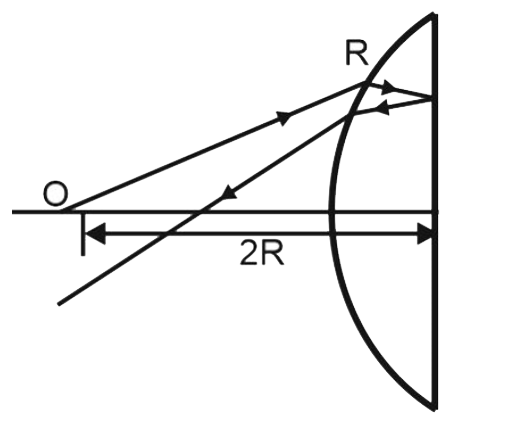
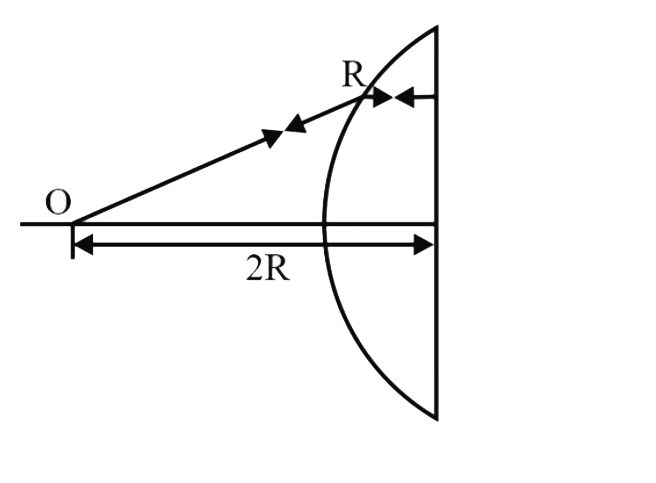
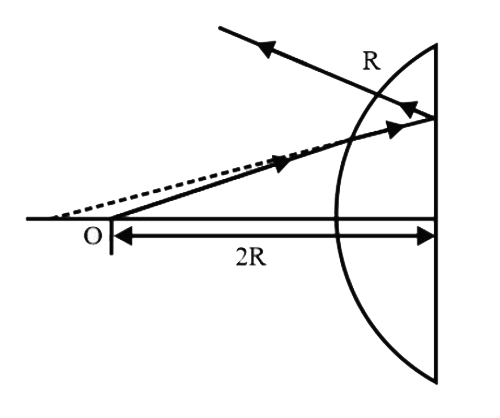
D. None of the above

Answer

B

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the Lens Configuration
We have a thin plano-convex lens with its plane surface silvered. The radius of curvature of the curved part is denoted as \( R \). The refractive index \( \mu \) of the lens is given as 1.5.

Step 2: Calculate the Focal Length of the Lens
Using the lens formula for a plano-convex lens:
\( \frac{1}{f} = (\mu - 1) \left( \frac{1}{R} - \frac{1}{\infty} \right) \)
Here, \( R \) is the radius of curvature of the curved surface, and since the plane surface is silvered, its radius of curvature is considered infinite.

Substituting the values:
\( \frac{1}{f} = (1.5 - 1) \left( \frac{1}{R} - 0 \right) = 0.5 \cdot \frac{1}{R} \)
This simplifies to:
\( \frac{1}{f} = \frac{0.5}{R} \implies f = 2R \)

Step 3: Determine the Object Position
The object is placed at a distance of \( 2R \) from the lens. Since the focal length \( f \) is \( 2R \), the object is positioned at \( 2f \).

Step 4: Analyze Ray Diagram
When the object is placed at \( 2R \) (which is \( 2f \)), we can use the lens properties to determine the image formation:
1. A ray parallel to the principal axis will pass through the focal point after refraction.
2. A ray passing through the focal point will emerge parallel to the principal axis.
3. Since the plane surface is silvered, the rays will reflect back through the lens.

Step 5: Image Formation
Since the object is at \( 2f \), the image will be formed at the same distance on the opposite side of the lens. The rays will retrace their path after reflecting off the silvered surface.

Conclusion
The correct ray diagram for the given configuration, where the object is placed at \( O \) (at a distance of \( 2R \)), will show that the image is formed at the same distance \( 2R \) on the opposite side of the lens.

Final Answer
The correct option is B.

---