A balloon moving in a straight line passes vertically above two points A and B on a horizontal plane 300 ft apart. When above A it has an altitude of as seen from A. The distance of B it has an altitude of as seen from A. The distance of B from the point C where it will touch the plane is
The correct Answer is:A
To solve the problem step by step, we will use trigonometric relationships in right triangles formed by the balloon's altitude and the horizontal distances between points A, B, and C.
Step 1: Understand the Configuration
We have two points A and B on a horizontal plane, 300 ft apart. The balloon is at a certain altitude above these points, and we need to find the distance from point B to the point C where the balloon will touch the plane.
Step 2: Set Up the Triangles
1. Triangle ABE: When the balloon is directly above point A, it forms a right triangle with:
- Angle at A (viewing angle from A to the balloon) = 45°
- Opposite side (altitude of balloon above A) = H
- Adjacent side (distance from A to B) = 300 ft
2. Triangle BEC: When the balloon is directly above point B, it forms another right triangle with:
- Angle at B (viewing angle from A to the balloon) = 30°
- Opposite side (altitude of balloon above B) = h
- Adjacent side (distance from B to C) = x (the distance we want to find)
Step 3: Use Trigonometric Ratios
1. From Triangle ABE:
- Using the tangent function:
tan(45∘)=H300
- Since tan(45∘)=1, we have:
H=300 ft
2. From Triangle BEC:
- Using the tangent function:
tan(30∘)=hx
- We know tan(30∘)=1√3, so:
1√3=hx⟹h=x√3
Step 4: Relate the Heights
Since the balloon is moving in a straight line, we can express the height h in terms of H:
- The height difference between points A and B is:
H−h=300−h
Step 5: Substitute for h
Substituting h from the previous step:
300−x√3=(the vertical distance from A to B)
Step 6: Use Similar Triangles
From triangles ABE and BEC being similar:
H300=hx
Substituting the values we have:
300300=x√3x
This simplifies to:
1=1√3⟹x=300√3−300
Step 7: Solve for x
Now we can express x:
x=300(√3−1)
Step 8: Final Calculation
To find the distance from B to C:
x=150(2√3−2)=150(2√3+2)
Final Answer
The distance from point B to point C is:
x=150(2+√3) feet
We have two points A and B on a horizontal plane, 300 ft apart. The balloon is at a certain altitude above these points, and we need to find the distance from point B to the point C where the balloon will touch the plane.
1. Triangle ABE: When the balloon is directly above point A, it forms a right triangle with:
- Angle at A (viewing angle from A to the balloon) = 45°
- Opposite side (altitude of balloon above A) = H
- Adjacent side (distance from A to B) = 300 ft
- Angle at B (viewing angle from A to the balloon) = 30°
- Opposite side (altitude of balloon above B) = h
- Adjacent side (distance from B to C) = x (the distance we want to find)
1. From Triangle ABE:
- Using the tangent function:
tan(45∘)=H300
- Since tan(45∘)=1, we have:
H=300 ft
- Using the tangent function:
tan(30∘)=hx
- We know tan(30∘)=1√3, so:
1√3=hx⟹h=x√3
Since the balloon is moving in a straight line, we can express the height h in terms of H:
- The height difference between points A and B is:
H−h=300−h
Substituting h from the previous step:
300−x√3=(the vertical distance from A to B)
From triangles ABE and BEC being similar:
H300=hx
Substituting the values we have:
300300=x√3x
This simplifies to:
1=1√3⟹x=300√3−300
Now we can express x:
x=300(√3−1)
To find the distance from B to C:
x=150(2√3−2)=150(2√3+2)
The distance from point B to point C is:
x=150(2+√3) feet
Similar Questions
A balloon moving in a straight line passes vertically above two points A and B on a horizontal plane 10ft apart. When above A the balloon has an angle of elevation of 60∘ as seen from B. When above B it has an angle of elevation of 45∘ as seen from A. The distance of B from the point C where it will touch the plane is
View SolutionA balloon moving in a straight line passes vertically above two points A and B on a horizontal plane 1000ft apart. When above A it has an altitude of 60∘ as seen from B, when above B, 30∘ as seen from A. Find the distance from A at which it will strike the plane.
View SolutionA line passes through two points A(2,−3,−1) and B(8,−1,2). The coordinates of a point on this lie at distance of 14 units from a are
View SolutionThe angle of elevation of the loop of a vertical tower standing on a horizontal plane is observed to be 45∘ from a point A on the plane. Let B be the point 30m vertically above the point A. If the angle of elevation of the top of the tower from B be 30∘, then the distance (in m) of the foot of the lower from the point A is:
View SolutionA balloon is moving up in air vertically above a point A on the ground. When it is at a height h1, a girl standing at a distance (point B) from A (see figure) sees it at an angle 45∘ with respect to the vertical. When the balloon climbs up a further height h2, it is seen at an angle 60∘ with respect to the vertical if the girl moves further by a distance 2.464d (point C). Then the height h2 is (give tan30∘=0.5774)
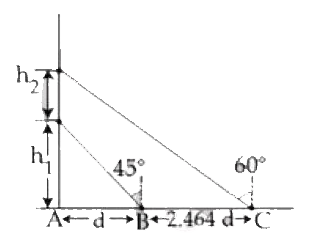
View SolutionAn aeroplane flying at a height 300 metre above the ground passes vertically above another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 60∘ and 45∘ respectively. Then the height of the lower plane from the ground in metres is
View SolutionA vertical pole of length 15 m standing on the point A. ABC are points on horizontal ground forming a triangle with ∠A=90∘.
If AB = 6m and AC = 8m and a point 'D' (on horizontal plane) is equidistant from A, B, C. Find distance of D from top of the pole
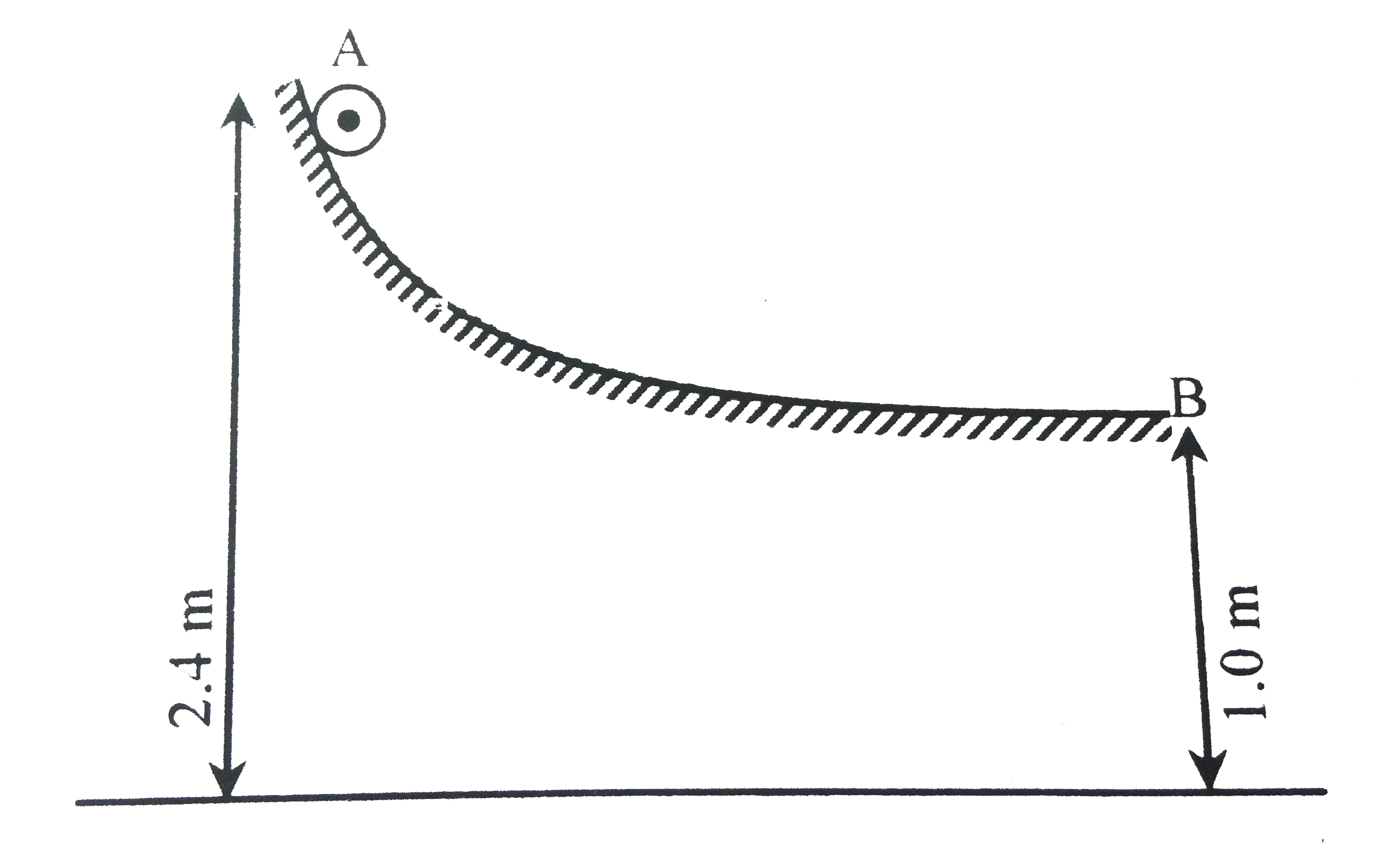
View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is 1.0 meter above the ground level and the top of the track is 2.4 meter above the ground. Find the distance on the ground with respect to a point B( which is vetically below the end A of the track as shown in fig.) where the sphere lands.
 .
.
(A) 1m
(B) 2m
( C) 3m
(D) 4m.
View SolutionA man observes that when he moves up a distance c metres on a slope, the angle of depression of a point on the horizontal plane from the base of the slope is 300, and when he moves up further a distance c metres, the angle of depression of that point is 450. The angle of inclination of the slope with the horizontal is.
View SolutionA helicopter is flying horizontally at an altitude of 2km with a speed of 100ms−1 . A packet is dropped from it. The horizontal distance between the point where the packet is dropped and the point where it hits the ground is (g=10ms−2)
View Solution
