A balloon moving in a straight line passes vertically above two points A and B on a horizontal plane 1000ft apart. When above A it has an altitude of 60∘ as seen from B, when above B, 30∘ as seen from A. Find the distance from A at which it will strike the plane.
The correct Answer is:1500 ft
To solve the problem step-by-step, we can follow these steps:
Step 1: Understand the Problem
We have two points A and B on a horizontal plane that are 1000 feet apart. A balloon passes directly above these points, and we need to find the distance from point A to where the balloon will strike the plane.
Step 2: Draw a Diagram
Draw a horizontal line representing the ground with points A and B, 1000 feet apart. Above point A, the balloon has an altitude that makes a 60° angle with point B. Above point B, it makes a 30° angle with point A.
Step 3: Define Variables
Let:
- H = height of the balloon when it is directly above point A.
- D = distance from point A to the point where the balloon will strike the plane.
Step 4: Use Trigonometry for Triangle ABE
In triangle ABE (where E is the position of the balloon directly above A):
- The angle at B is 60°.
- The opposite side (height of the balloon) is H.
- The adjacent side (distance from A to B) is 1000 feet.
Using the tangent function:
tan(60°)=H1000
H=1000⋅tan(60°)=1000⋅√3
Step 5: Use Trigonometry for Triangle ABE
In triangle ABE (where E is the position of the balloon directly above B):
- The angle at A is 30°.
- The opposite side (height of the balloon) is H−h where h is the height of the balloon above point B.
- The adjacent side (distance from A to B) is 1000 feet.
Using the tangent function:
tan(30°)=H−h1000
H−h=1000⋅tan(30°)=1000⋅1√3
Step 6: Set Up the Equation
From the two equations we derived:
1. H=1000√3
2. H−h=1000√3
Substituting H into the second equation:
1000√3−h=1000√3
h=1000√3−1000√3
Step 7: Simplify the Height
To simplify h:
h=1000(√3−1√3)=1000(3−1√3)=1000⋅2√3=2000√3
Step 8: Find the Distance D
Now, we can find the distance D from point A to the point where the balloon will strike the plane. The distance D can be expressed as:
D=1000+x
where x is the horizontal distance from point B to the point where the balloon strikes the plane.
Using similar triangles:
H1000=hx
Substituting the values of H and h:
1000√31000=2000√3x
Cross-multiplying gives:
x⋅√3=2000
x=2000√3≈1154.7 feet
Step 9: Calculate Total Distance D
Now, substituting back to find D:
D=1000+x=1000+2000√3≈1000+1154.7≈2154.7 feet
Final Answer
The distance from point A at which the balloon will strike the plane is approximately 2154.7 feet.
---
We have two points A and B on a horizontal plane that are 1000 feet apart. A balloon passes directly above these points, and we need to find the distance from point A to where the balloon will strike the plane.
Draw a horizontal line representing the ground with points A and B, 1000 feet apart. Above point A, the balloon has an altitude that makes a 60° angle with point B. Above point B, it makes a 30° angle with point A.
Let:
- H = height of the balloon when it is directly above point A.
- D = distance from point A to the point where the balloon will strike the plane.
In triangle ABE (where E is the position of the balloon directly above A):
- The angle at B is 60°.
- The opposite side (height of the balloon) is H.
- The adjacent side (distance from A to B) is 1000 feet.
tan(60°)=H1000
H=1000⋅tan(60°)=1000⋅√3
In triangle ABE (where E is the position of the balloon directly above B):
- The angle at A is 30°.
- The opposite side (height of the balloon) is H−h where h is the height of the balloon above point B.
- The adjacent side (distance from A to B) is 1000 feet.
tan(30°)=H−h1000
H−h=1000⋅tan(30°)=1000⋅1√3
From the two equations we derived:
1. H=1000√3
2. H−h=1000√3
1000√3−h=1000√3
h=1000√3−1000√3
To simplify h:
h=1000(√3−1√3)=1000(3−1√3)=1000⋅2√3=2000√3
Now, we can find the distance D from point A to the point where the balloon will strike the plane. The distance D can be expressed as:
D=1000+x
where x is the horizontal distance from point B to the point where the balloon strikes the plane.
H1000=hx
Substituting the values of H and h:
1000√31000=2000√3x
Cross-multiplying gives:
x⋅√3=2000
x=2000√3≈1154.7 feet
Now, substituting back to find D:
D=1000+x=1000+2000√3≈1000+1154.7≈2154.7 feet
The distance from point A at which the balloon will strike the plane is approximately 2154.7 feet.
Similar Questions
A balloon moving in a straight line passes vertically above two points A and B on a horizontal plane 300 ft apart. When above A it has an altitude of 30∘ as seen from A. The distance of B it has an altitude of 30∘ as seen from A. The distance of B from the point C where it will touch the plane is
View SolutionA balloon moving in a straight line passes vertically above two points A and B on a horizontal plane 10ft apart. When above A the balloon has an angle of elevation of 60∘ as seen from B. When above B it has an angle of elevation of 45∘ as seen from A. The distance of B from the point C where it will touch the plane is
View SolutionWhen a coin placed in a bowl of water and seen from above, it appears :
View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is 1.0 meter above the ground level and the top of the track is 2.4 meter above the ground. Find the distance on the ground with respect to a point B( which is vetically below the end A of the track as shown in fig.) where the sphere lands.
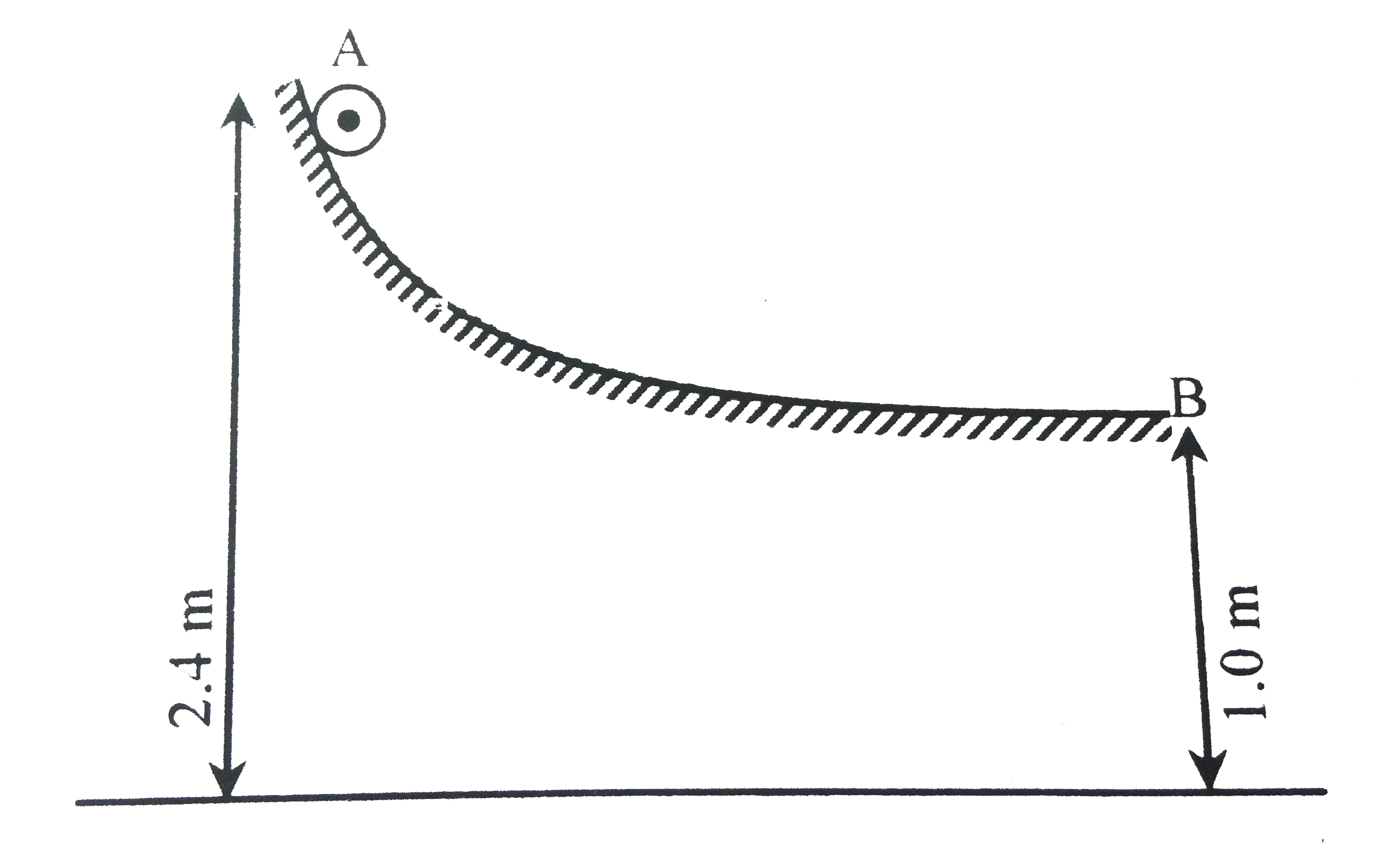 .
.
(A) 1m
(B) 2m
( C) 3m
(D) 4m.
View SolutionAn aeroplane, when 3000 m high, passes vertically above anthoer aeroplane at an instant when the angles of elevation of the two planes from the same point on the ground are 45∘ and 60∘ respectively. Find the vertical distance between the tow planes.
View SolutionAn aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60∘ and 45∘ respectively. Find the vertical distance between the aeroplanes at that instant.
View SolutionAn aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 600&450 respectively. Find the vertical distance between the aeroplanes at that instant.
View SolutionIn figure, a point source S is placed at a height h above the plane mirror in a medium of refractive index μ.
a. Find the number of images seen for normal view.
b. Find the distance between the images.

View SolutionA body moves along a straight line OAB simple harmonically. It has zero velocity at the points A and B which are at distances 'a' and b'respectivelyom0' and has velocity 'V' when halfway between them then the period of SHM
View SolutionTwo vertical poles of height 10 m and 40 m stand apart on a horizontal plane. The height (in meters) of the point of intersection of the line joining the top of each pole to the foot of the other, from this horizontal plane is
View Solution
