A thin plastic of refractive index 1.6 is used to cover one of the slits of a double slit arrangement. The central point omn the screen is now occupied by what would have been the 7th bright fringe before the plastic was used. If the wavelength of light is 600 nm, what is the thickness ( in μm ) of the plastic?
7
4
8
6
The correct Answer is:A
To solve the problem, we need to determine the thickness of the plastic that causes the central maximum to shift to the position of the 7th bright fringe in a double slit interference pattern.
1. Understanding Path Difference:
When a thin plastic sheet of refractive index μ is placed in front of one of the slits, it changes the optical path length for the light passing through that slit. The optical path length through the plastic is given by μt, where t is the thickness of the plastic.
2. Calculating the Path Difference:
The path difference Δ introduced by the plastic is:
Δ=μt−t=(μ−1)t
Given that μ=1.6, we can substitute this value:
Δ=(1.6−1)t=0.6t
3. Condition for Bright Fringe:
The central maximum now coincides with the position of the 7th bright fringe. The path difference for the 7th bright fringe is given by:
Δ=7λ
where λ is the wavelength of light. Given λ=600nm=600×10−9m.
4. Setting the Path Differences Equal:
To find the thickness t, we set the path difference due to the plastic equal to the path difference for the 7th fringe:
0.6t=7λ
Substituting the value of λ:
0.6t=7×600×10−9
5. Solving for Thickness t:
Rearranging the equation to solve for t:
t=7×600×10−90.6
Calculating the right-hand side:
t=4200×10−90.6=7000×10−9m=7×10−6m
Converting to micrometers:
t=7μm
Final Answer:
The thickness of the plastic is 7μm.
When a thin plastic sheet of refractive index μ is placed in front of one of the slits, it changes the optical path length for the light passing through that slit. The optical path length through the plastic is given by μt, where t is the thickness of the plastic.
The path difference Δ introduced by the plastic is:
Δ=μt−t=(μ−1)t
Given that μ=1.6, we can substitute this value:
Δ=(1.6−1)t=0.6t
The central maximum now coincides with the position of the 7th bright fringe. The path difference for the 7th bright fringe is given by:
Δ=7λ
where λ is the wavelength of light. Given λ=600nm=600×10−9m.
To find the thickness t, we set the path difference due to the plastic equal to the path difference for the 7th fringe:
0.6t=7λ
Substituting the value of λ:
0.6t=7×600×10−9
Rearranging the equation to solve for t:
t=7×600×10−90.6
Calculating the right-hand side:
t=4200×10−90.6=7000×10−9m=7×10−6m
Converting to micrometers:
t=7μm
The thickness of the plastic is 7μm.
Similar Questions
In young's double-slit experiment, both the slits produce equal intensities on a screen. A 100% transparent thin film of refractive index μ=1.5 is kept in front of one of the slits, due to which the intensity at the point O on the screen becomes 75% of its initial value. If the wavelength of monochromatic light is 720 nm, then what is the minimum thickness (in nm) of the film?
View SolutionA very thin sheet of plastic having refractive index μ=1.5 covers one slit of a double slit apparatus illuminated by 700 nm light . The central point on the screen , instead of being maximum , is dark . What is the possible thickness of the plastic in (nm) ?
View SolutionOne slit of a double slits experiment is covered by a thin glass plate of refractive index1.4and the other by a thin glass plate of refractive index1.7 .The point on the screen ,where central bright fringe was formed before the introduction of the glass sheets,is now occupied by the 15thbright fringe.Assuming that both the glass plates have same thickness and wavelength of light used in 4800Å ,find the their thickness.
View SolutionWhen the plastic thin film of refractive index 1.45is placed in the path of one of the interfering waves then the central fringe is displaced through width of five fringes.The thickness of the film will be ,if the wavelength of light is5890Å
View SolutionIn YDSE, the sources is red ligth of wavelength 7×10−7m. When a thin glass plate of refractive index 1.5 is put in the path of one of the interfering beams, the central bright fringe shifts by 10−3 m to the position previously occupied by the 5th bright fringe.
If the source is now changed to green light of wavelength 10−7m, the central fringe shifts to a position initially occupied by the sixth bright fringe due to red ligth. What will be refractive index of glass plate for the second ligth for changed source of ligth?
View SolutionA thin glass plate of thickness t and refractive index μ is inserted between screen and one of the slits in a young's experiment. If the intensity at the centre of the screen is I, what was the intensity at the same point prior to the introduction of the sheet.
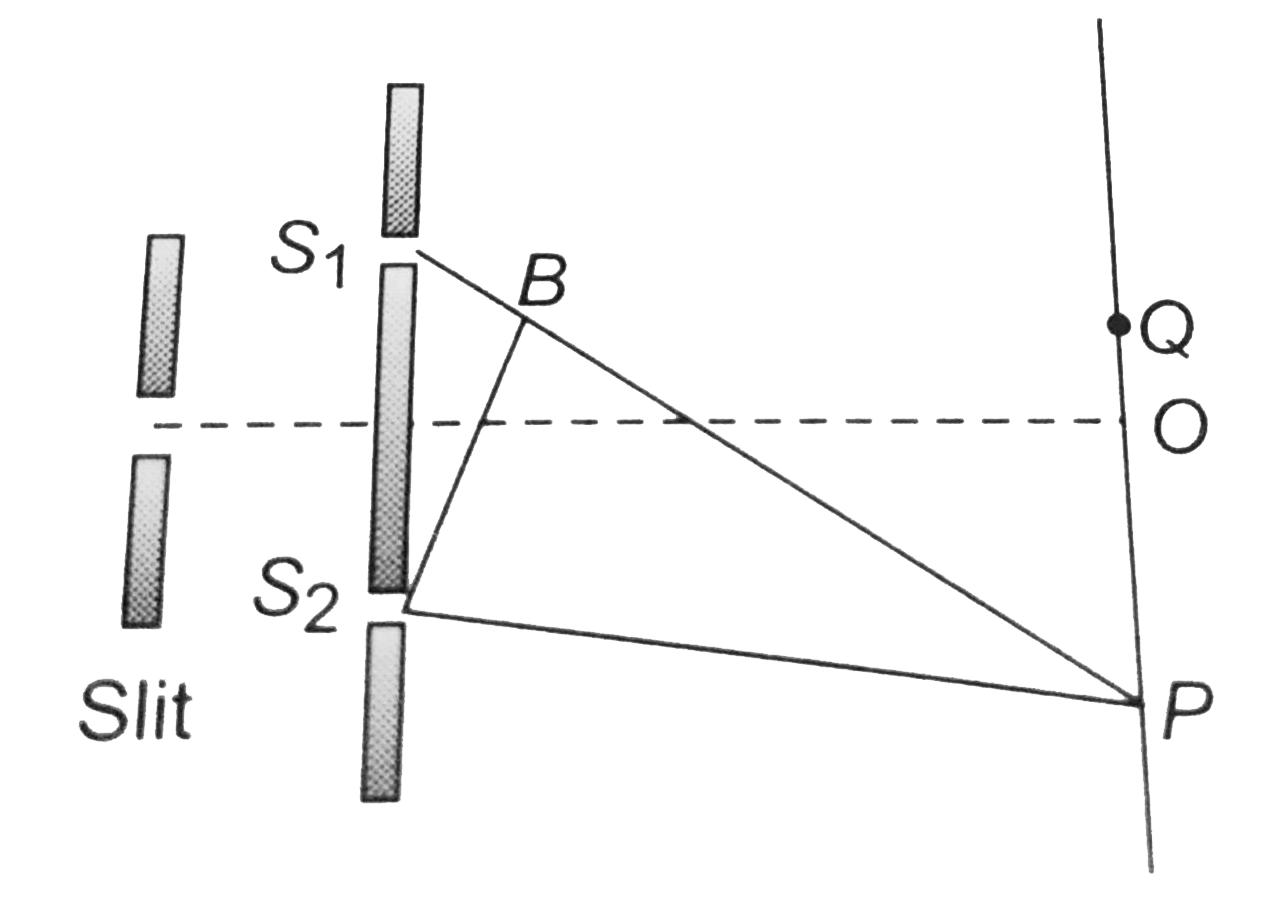
View SolutionIn the figure is shown Young's double slit experiment. Q is the position of the first bright fringe on the right side of O. P is the 11th bright fringe on the other side, as measured from Q. If the wavelength of the light used is 600nm. Then S1B will be equal to
View SolutionIn a double-slit experiment, fringes are produced using light of wavelength 4800A∘. One slit is covered by a thin plate of glass of refractive index 1.4 and the other slit by another plate of glass of double thickness and of refractive index 1.7. On doing so, the central bright fringe shifts to a position originally occupied by the fifth bright fringe from the center. find the thickness of the glass plates.
View SolutionIn Young's double slit experiment a mica plate of refractive index μ is introduced in the path of light coming from one of the slit . If the central bright fringe gets shifted to the point originally occupied by the fourth bright fringe, then the thickness of the mica plate will be (symbols have their usual meaning )
View SolutionWith two slits spaced 0.2 mm apart and a screen at a distance of 1 m, the third bright fringe is found to be at 7.5 mm from the central fringe. The wavelength of light used is
View Solution
