A very thin sheet of plastic having refractive index μ=1.5 covers one slit of a double slit apparatus illuminated by 700 nm light . The central point on the screen , instead of being maximum , is dark . What is the possible thickness of the plastic in (nm) ?
700 nm
1400 nm
350nm
2100 nm
The correct Answer is:A, D
To solve the problem, we need to determine the thickness of the plastic sheet that causes a dark fringe at the central point on the screen in a double slit experiment. This occurs when the additional path difference introduced by the plastic sheet is equal to half the wavelength of the light used.
1. Identify the Given Values:
- Refractive index of plastic, μ=1.5
- Wavelength of light, λ=700nm
2. Understand the Condition for Dark Fringe:
- A dark fringe occurs when the additional path difference caused by the plastic sheet is equal to λ2.
3. Calculate the Additional Path Difference:
- The additional path difference Δx due to the plastic sheet can be expressed as:
Δx=(μ−1)t
where t is the thickness of the plastic sheet.
4. Set Up the Equation:
- Since we want the additional path difference to be λ2:
(μ−1)t=λ2
5. Substitute the Values:
- Substitute μ=1.5 and λ=700nm:
(1.5−1)t=700nm2
- This simplifies to:
0.5t=350nm
6. Solve for Thickness t:
- Rearranging gives:
t=350nm0.5=700nm
Final Answer:
The possible thickness of the plastic sheet is t=700nm.
---
- Refractive index of plastic, μ=1.5
- Wavelength of light, λ=700nm
- A dark fringe occurs when the additional path difference caused by the plastic sheet is equal to λ2.
- The additional path difference Δx due to the plastic sheet can be expressed as:
Δx=(μ−1)t
where t is the thickness of the plastic sheet.
- Since we want the additional path difference to be λ2:
(μ−1)t=λ2
- Substitute μ=1.5 and λ=700nm:
(1.5−1)t=700nm2
- This simplifies to:
0.5t=350nm
- Rearranging gives:
t=350nm0.5=700nm
The possible thickness of the plastic sheet is t=700nm.
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic
48 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A thin plastic of refractive index 1.6 is used to cover one of the slits of a double slit arrangement. The central point omn the screen is now occupied by what would have been the 7th bright fringe before the plastic was used. If the wavelength of light is 600 nm, what is the thickness ( in μm ) of the plastic?
View SolutionA thin mica sheet of thickness 2×10−6m and refractive index (μ=1.5) is introduced in the path of the first wave. The wavelength of the wave used is 5000Å. The central bright maximum will shift
View SolutionA thin mica sheet of thickness 2×10−6m and refractive index (μ=1.5) is introduced in the path of the first wave. The wavelength of the wave used is 5000Å. The central bright maximum will shift
View SolutionA thin mica sheet of thickness 2×10−6m and refractive index (μ=1.5) is introduced in the path of the first wave. The wavelength of the wave used is 5000Å. The central bright maximum will shift
View SolutionIn YDSE a=2mm, D = 2m, λ=500 nm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
View SolutionA thin mica sheet of thickness 4×10−6 m and refractive index (μ=1.5) is introduced in the path of the light from upper slit. The wavelength of the wave used is 5000Å The central bright maximum will shift
View SolutionA double slit is illuminated by the light of wavelength 12000A .The slits are 0.1 cm apart and the screen is placed one metre away.calculate the angular posiyion of 10 maximum in radians ?
View SolutionIn young's double-slit experiment, both the slits produce equal intensities on a screen. A 100% transparent thin film of refractive index μ=1.5 is kept in front of one of the slits, due to which the intensity at the point O on the screen becomes 75% of its initial value. If the wavelength of monochromatic light is 720 nm, then what is the minimum thickness (in nm) of the film?
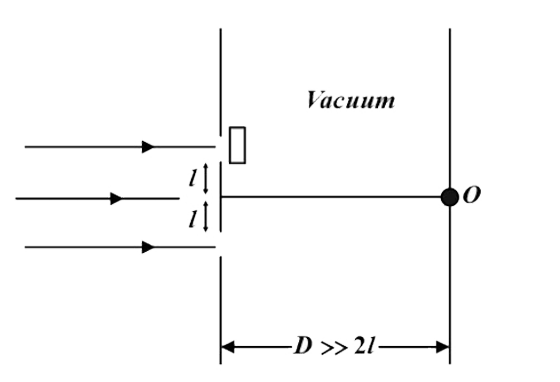
View SolutionTwo transparent slabs having equal thickness 0.45 mm and refractive indices 1.40 and 1.42 are pasted on the two slits of a double slit apparatus. The separation of slits equals 1mm. Wavelength of light used equals 600 nm. The screen is placed at a distance 1m from the plane of the slits. The central maxima from the centre of the screen is [in mm]
View SolutionIn a doulble slit experiment when a thin film of thickness t having refractive index μ is introduced in from of one of the slits, the maximum at the centre of the fringe pattern shifts by one width. The value of t is (λ is the wavelength of the light used)
View Solution
