Consider the interference at P between waves emitting from three coherent sources in the same phase located at S1 , S2 and S3 . If the intensity due to each source is I0=12Wm−2 at P and d22D=λ3 then what will be the resultant intensity (in Wm−2 ) at P?
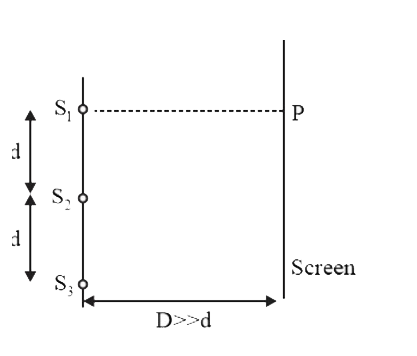
The correct Answer is:36
Step by step video & image solution for Consider the interference at P between waves emitting from three coherent sources in the same phase located at S_(1) , S_(2) and S_(3) . If the intensity due to each source is I_(0)=12Wm^(-2) at P and (d^(2))/(2D)=(lamda)/(3) then what will be the resultant intensity (in Wm^(-2) ) at P? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Consider an interference pattern between two coherent sources. If I1andI2 be intensities at points where the phase difference are π3and2π3 and respectively , then the intensity at maxima is
View SolutionTwo coherent monochormatic light source are located at two vertices of an equilateral trangle. If the intensity due to each of the source independently is 1Wm−2 at the third vertex. The resultant intensity due to both the sources at that point (i.e at the third vertex) is (in Wm−2 )
View SolutionTwo waves of equal amplitude a from two coherent sources (S1&S2) interfere at a point R such that S2R−S1R=1.5λThe intensity at point R Would be
View SolutionThe intensity of sound from a point source is 1.0×10−8Wm−2, at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source ?
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
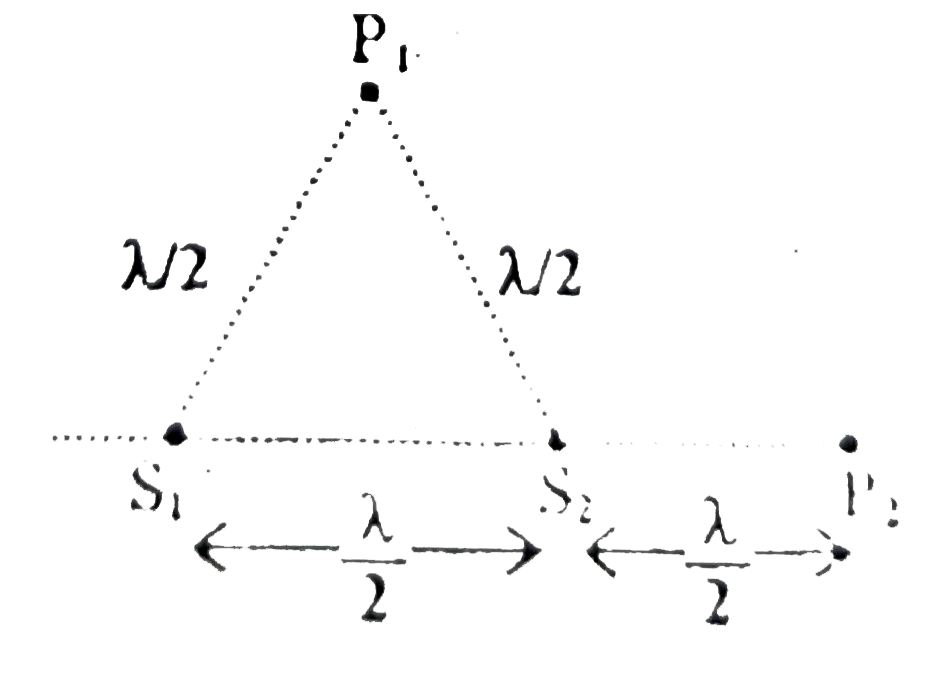
View SolutionWhen two waves of intensities l1andl2 coming from coherent sources interfere at a point P, where phase difference is ϕ, then resultant intensity (lres) at point P would be
View SolutionIn the figure , the intensity of waves arriving at D from two coherent soucrces s1ands2isI0. The wavelength of the wave is λ=4m . Resultant intensity at D will be

View SolutionFour monochromatic and coherent sources of light emitting waves in phase at placed on y axis at y = 0, a, 2a and 3a. If the intensity of wave reaching at point P far away on y axis from each of the source is almost the same and equal to I0, then the resultant intensity at P for a=λ8 is nI0. The value of [n] is.
Here [] is greatest integer funciton.
View SolutionTwo coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View Solution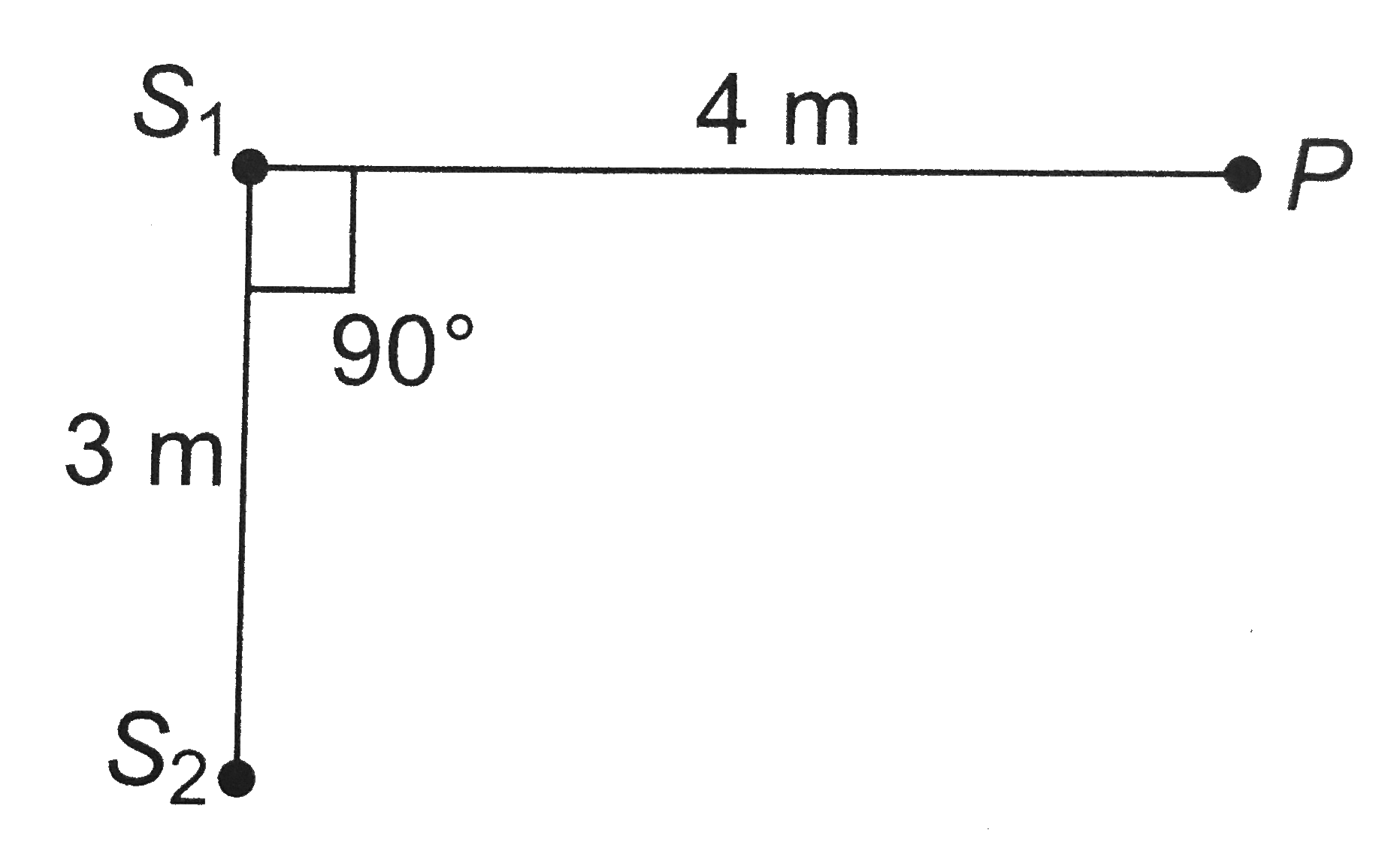
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P is
View Solution
