In a shooting competition a man can score 5, 4, 3, 2, 1 or 0 points for each shot. Then the number of different ways in which he can score 10 in seven shots is
6538
6648
6468
6236
The correct Answer is:A
To solve the problem of finding the number of different ways a man can score 10 points in 7 shots, where he can score 5, 4, 3, 2, 1, or 0 points for each shot, we can use generating functions.
Step 1: Define the generating function
The scores possible for each shot can be represented by the generating function:
f(x)=x0+x1+x2+x3+x4+x5
This function represents the scores from 0 to 5 points.
Step 2: Raise the generating function to the power of 7
Since there are 7 shots, we raise the generating function to the power of 7:
f(x)7=(x0+x1+x2+x3+x4+x5)7
Step 3: Simplify the generating function
We can rewrite the generating function as:
f(x)=1−x61−x
Thus,
f(x)7=(1−x61−x)7=(1−x6)7(1−x)−7
Step 4: Expand using the binomial theorem
Using the binomial theorem, we can expand both parts:
1. (1−x6)7 can be expanded as:
7∑k=0(7k)(−1)kx6k
2. (1−x)−7 can be expanded as:
∞∑m=0(m+66)xm
Step 5: Find the coefficient of x10
To find the coefficient of x10 in f(x)7, we need to find the terms where 6k+m=10. This gives us:
m=10−6k
The possible values for k are 0, 1, and 2 (since 6k must be less than or equal to 10).
Case 1: k=0
m=10⟹Coefficient=(70)(10+66)=1⋅(166)=8008
Case 2: k=1
m=4⟹Coefficient=(71)(−1)1(4+66)=−7⋅(106)=−7⋅210=−1470
Case 3: k=2
m=−2⟹Coefficient=(72)(−1)2(−2+66)=21⋅0=0
Step 6: Sum the coefficients
Now we sum the coefficients from all cases:
8008−1470+0=6538
Final Answer
Thus, the number of different ways in which he can score 10 in 7 shots is:
6538
The scores possible for each shot can be represented by the generating function:
f(x)=x0+x1+x2+x3+x4+x5
This function represents the scores from 0 to 5 points.
Since there are 7 shots, we raise the generating function to the power of 7:
f(x)7=(x0+x1+x2+x3+x4+x5)7
We can rewrite the generating function as:
f(x)=1−x61−x
Thus,
f(x)7=(1−x61−x)7=(1−x6)7(1−x)−7
Using the binomial theorem, we can expand both parts:
1. (1−x6)7 can be expanded as:
7∑k=0(7k)(−1)kx6k
2. (1−x)−7 can be expanded as:
∞∑m=0(m+66)xm
To find the coefficient of x10 in f(x)7, we need to find the terms where 6k+m=10. This gives us:
m=10−6k
The possible values for k are 0, 1, and 2 (since 6k must be less than or equal to 10).
m=10⟹Coefficient=(70)(10+66)=1⋅(166)=8008
m=4⟹Coefficient=(71)(−1)1(4+66)=−7⋅(106)=−7⋅210=−1470
m=−2⟹Coefficient=(72)(−1)2(−2+66)=21⋅0=0
Now we sum the coefficients from all cases:
8008−1470+0=6538
Thus, the number of different ways in which he can score 10 in 7 shots is:
6538
Similar Questions
A batsman can score 0,1,2,3,4 or 6 runs from a ball. The number of different sequences in which he can score exactly 30 runs in an over of six balls
View SolutionA person has 5 shirts, 4 coat and 7 ties . Number of ways in which he can wear them is
View SolutionA shopkeeper has 11 copies each of nine different books, then the number of ways in which atleast one book can be selected is
View Solution
A batsman can score 0, 2, 3, or 4 runs for each ball he receives. If N is the number of ways of scoring a total of 20 runs in one over of six balls, then N is divisible by :
i) 5
ii) 7
iii) 14
iv) 16
View SolutionNumber of ways in which 12 different things can be distributed in 3 groups, is
View SolutionSix cards are drawn one by one from a set of unlimited number of cards, each card is marked with numbers −1,0or1. Number of different ways in which they can be drawn if the sum of the numbers shown by them vanishes is
View Solution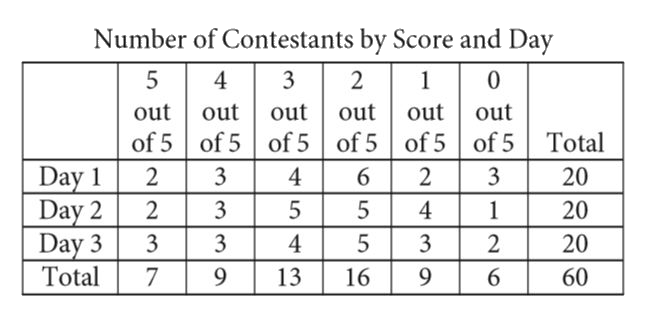
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
No contestant received the same score on two different days. If a contestant is selected at random, what is the probability that the selected contestant received a score of 5 on Day 2 or Day 3, given that the contestant received a score of 5 on one of the three days?
View SolutionThe number of ways in which 5 beads of different colours can be made into a necklace is
View SolutionFor examination, a candidate has to select 7 subjects from 3 different groups A, B, C which contain 4, 5, 6 subjects, respectively. The number of different way in which a candidate can make his selection if he has to select at least 2 subjects form each group is?
View SolutionThere are seven even greeting cards each of a different colour and seven envelopes of the same seven colours. Find the number of ways in which the cards can be put in the envelopes so that exactly four of the cards go into the envelopes of the right colour.
View Solution
