The time period of a physical pendulum about some pivot point is T. When we take another pivot point, opposite of the first one such that the centre of mass of the physical pendulum lies on the line joining these two pivot points, we obtain the same time period. If the two points are separated by a distance L, then the time period T is
2π√Lg
π√Lg
2π√L2g
π√2Lg
The correct Answer is:A
To find the time period T of a physical pendulum when the pivot points are separated by a distance L, we can follow these steps:
Step 1: Understand the Time Period of a Physical Pendulum
The time period T of a physical pendulum about a pivot point is given by the formula:
T=2π√Imgd
where:
- I is the moment of inertia about the pivot point,
- m is the mass of the pendulum,
- g is the acceleration due to gravity,
- d is the distance from the pivot point to the center of mass.
Step 2: Define the Two Pivot Points
Let’s denote the first pivot point as O and the second pivot point as O′. The distance between these two points is L. The center of mass (CM) of the pendulum lies on the line joining these two pivot points.
Step 3: Calculate the Moment of Inertia about Each Pivot Point
1. For the first pivot point O:
- Let the distance from the center of mass to point O be x.
- The moment of inertia about point O is given by:
IO=ICM+mx2
where ICM is the moment of inertia about the center of mass.
2. For the second pivot point O′:
- The distance from the center of mass to point O′ is L−x.
- The moment of inertia about point O′ is given by:
IO′=ICM+m(L−x)2
Step 4: Set Up the Time Period Equations
Using the time period formula for both pivot points:
1. For pivot point O:
T=2π√IOmgx=2π√ICM+mx2mgx
2. For pivot point O′:
T′=2π√IO′mg(L−x)=2π√ICM+m(L−x)2mg(L−x)
Step 5: Equate the Time Periods
Since it is given that T=T′:
√ICM+mx2mgx=√ICM+m(L−x)2mg(L−x)
Step 6: Square Both Sides and Simplify
Squaring both sides gives:
ICM+mx2mgx=ICM+m(L−x)2mg(L−x)
Cross-multiplying and simplifying leads to:
(ICM+mx2)(L−x)=(ICM+m(L−x)2)x
Step 7: Solve for ICM
Rearranging terms and solving for ICM leads to:
ICM=mx(L−x)
Step 8: Substitute ICM Back into the Time Period Formula
Substituting ICM back into the time period equation:
T=2π√mx(L−x)+mx2mgx=2π√mLxmgx=2π√Lg
Final Result
Thus, the time period T is:
T=2π√Lg
The time period T of a physical pendulum about a pivot point is given by the formula:
T=2π√Imgd
where:
- I is the moment of inertia about the pivot point,
- m is the mass of the pendulum,
- g is the acceleration due to gravity,
- d is the distance from the pivot point to the center of mass.
Let’s denote the first pivot point as O and the second pivot point as O′. The distance between these two points is L. The center of mass (CM) of the pendulum lies on the line joining these two pivot points.
1. For the first pivot point O:
- Let the distance from the center of mass to point O be x.
- The moment of inertia about point O is given by:
IO=ICM+mx2
where ICM is the moment of inertia about the center of mass.
- The distance from the center of mass to point O′ is L−x.
- The moment of inertia about point O′ is given by:
IO′=ICM+m(L−x)2
Using the time period formula for both pivot points:
1. For pivot point O:
T=2π√IOmgx=2π√ICM+mx2mgx
T′=2π√IO′mg(L−x)=2π√ICM+m(L−x)2mg(L−x)
Since it is given that T=T′:
√ICM+mx2mgx=√ICM+m(L−x)2mg(L−x)
Squaring both sides gives:
ICM+mx2mgx=ICM+m(L−x)2mg(L−x)
Cross-multiplying and simplifying leads to:
(ICM+mx2)(L−x)=(ICM+m(L−x)2)x
Rearranging terms and solving for ICM leads to:
ICM=mx(L−x)
Substituting ICM back into the time period equation:
T=2π√mx(L−x)+mx2mgx=2π√mLxmgx=2π√Lg
Thus, the time period T is:
T=2π√Lg
Similar Questions
The temperature of a physical pendulum, whose time period is T, is raised by Δθ. The change in its time period is
View SolutionA body of mass m has time period T1 with one spring and has time period T2 with another spring. If both the springs are connected in parallel and same mass is used, then new time period T is given as
View Solution
Knowledge Check
- Question 1 - Select One
The ability to move from one point to another in the shortest period of time:
APowerBAgilityCSpeedDBalance
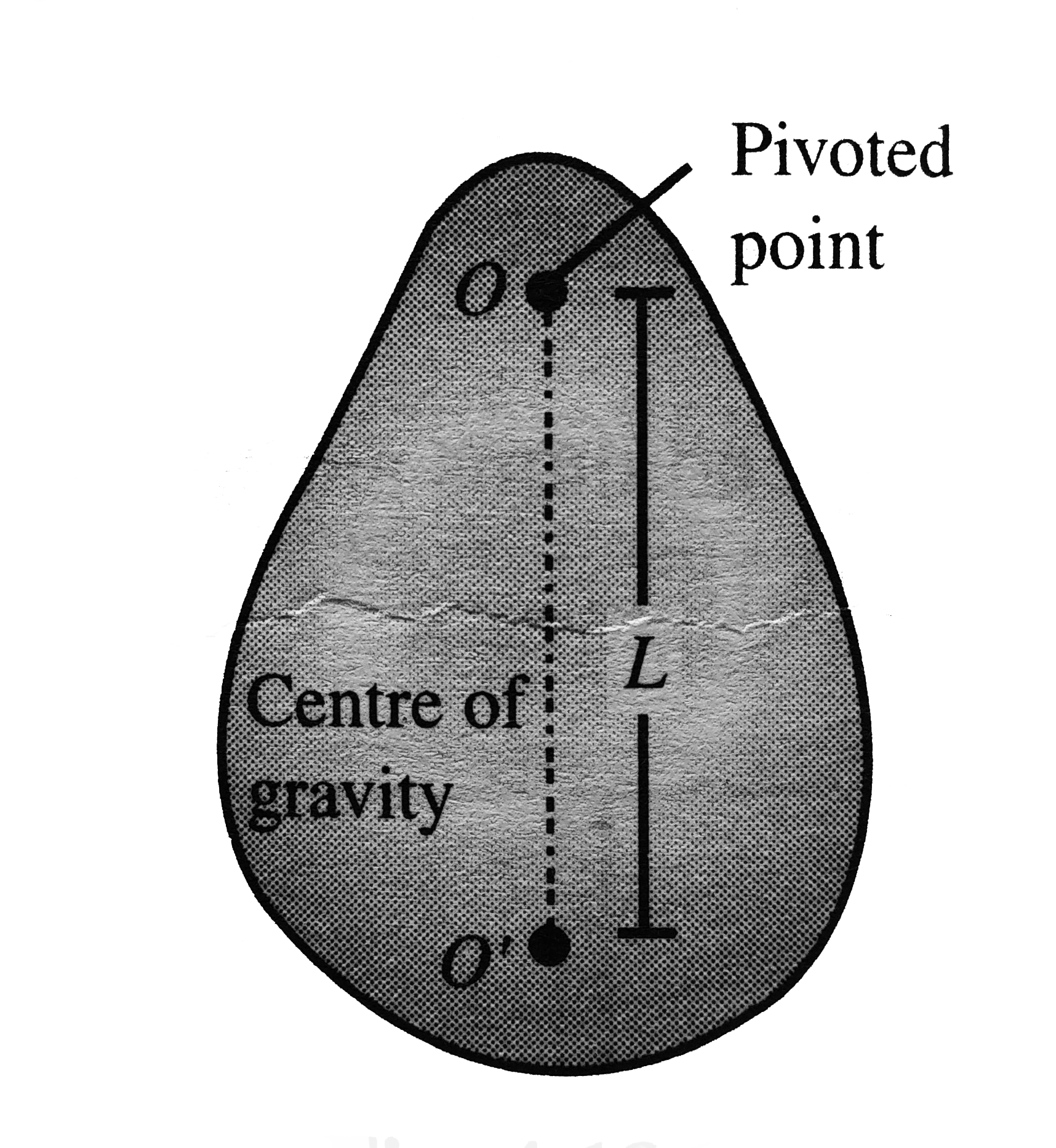
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.View SolutionIn physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. If an impulse J is applied at the centre of oscillation in the plane of oscillation, then angular velocity of the rod will be .
 View Solution
View SolutionThe distance between the point of suspension and the centre of gravity of a compound pendulum is l and the radius of gyration about the horizontal axis through the centre of gravity is k, then its time period will be
View SolutionThe time period of a bar pendulum when suspended at distance 30cm and 50cm from its centre of gravity comes out to be the same. If the mass of the body is 2kg. Find out its moment of inertia about an axis passing through first point.
_S01_024_Q01.png) View Solution
View SolutionA curve having the condition that the slope of the tangent at some point is two times the slope of the straight line joining the same point to the origin of coordinates is a/an
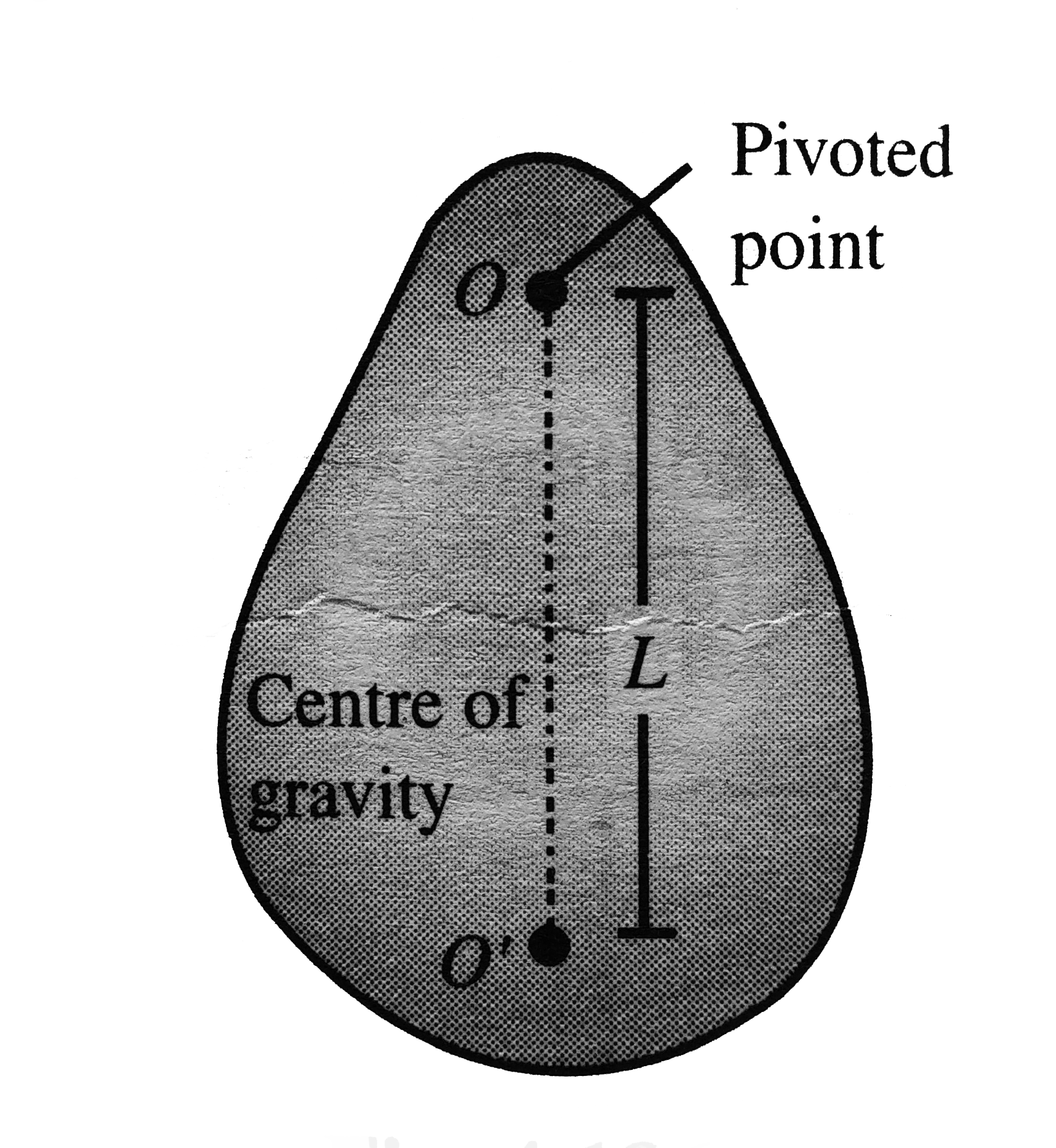
View SolutionIn physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. For the above question, locate the centre of oscillation.
 View Solution
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View Solution

