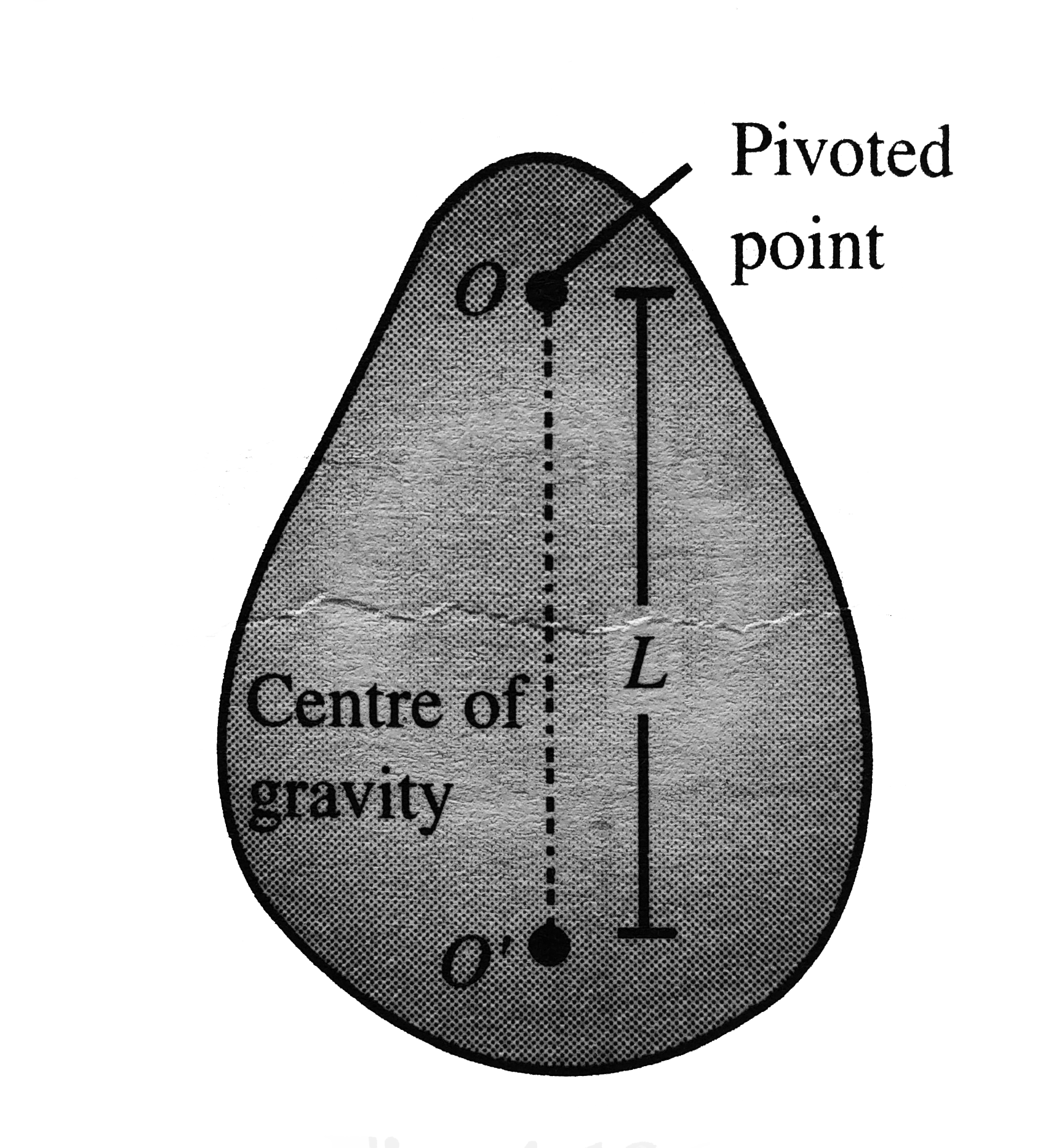
In physical pendulum, the time period for small oscillation is given by $T = 2 π \sqrt{\frac{I}{M g d}}$ where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
$T = 2 π \sqrt{\frac{I}{M g d}} = 2 π \sqrt{\frac{L}{g}}$ Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.

$2 π \sqrt{\frac{L}{g}}$

$π \sqrt{\frac{7 L}{3 g}}$

$2 π \sqrt{\frac{2 l}{3 g}}$

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

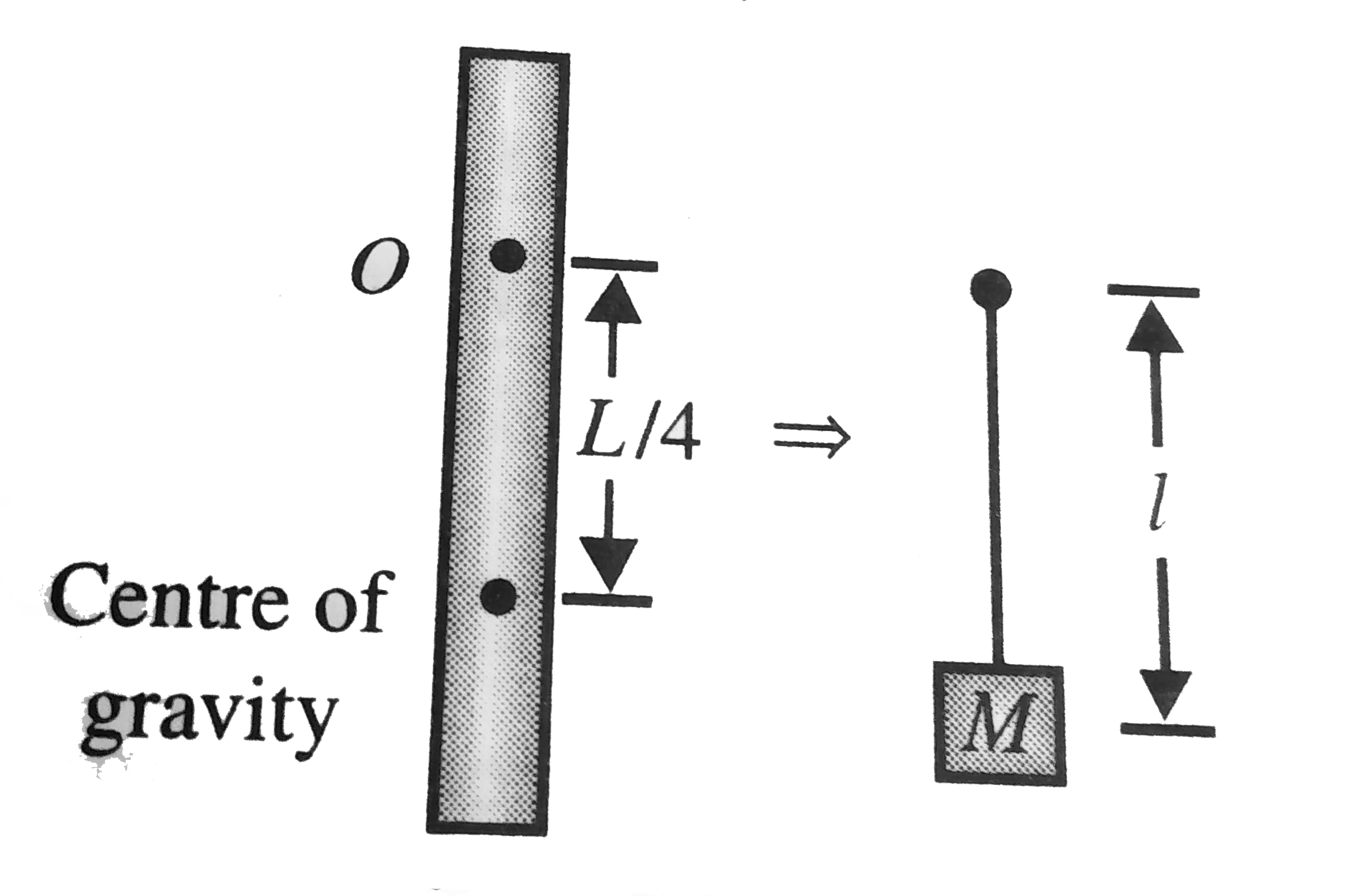
In the present case $d = \frac{L}{4}$
$I = \frac{M L^{2}}{12} + M {(\frac{L}{4})}^{2} = \frac{7}{48} M L^{2}$
So time period of the physical pendulum is $T = 2 π \sqrt{\frac{I}{M g d}}$
$= 2 π \sqrt{\frac{\frac{7}{48 M L^{2}}}{M g \times \frac{L}{4}}} = π \sqrt{\frac{7 L}{3 g}}$

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Knowledge Check

In physical pendulum, the time period for small oscillation is given by $T = 2 π \sqrt{\frac{I}{M g d}}$ where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
$T = 2 π \sqrt{\frac{I}{M g d}} = 2 π \sqrt{\frac{L}{g}}$ Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. For the above question, locate the centre of oscillation.

A $\frac{L}{4}$ from O (down)
B $\frac{L}{4}$ from O (up)
C $\frac{2 L}{3}$ from O (down)
D $\frac{7 L}{12}$ from O (down)
In physical pendulum, the time period for small oscillation is given by $T = 2 π \sqrt{\frac{I}{M g d}}$ where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
$T = 2 π \sqrt{\frac{I}{M g d}} = 2 π \sqrt{\frac{L}{g}}$ Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. If an impulse J is applied at the centre of oscillation in the plane of oscillation, then angular velocity of the rod will be .

A $\frac{4 J}{M L}$
B $\frac{2 J}{M L}$
C $\frac{3 J}{2 M L}$
D $\frac{J}{M L}$
In the figure shown ABCD is a lamina of mass $12 k g$ . The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is

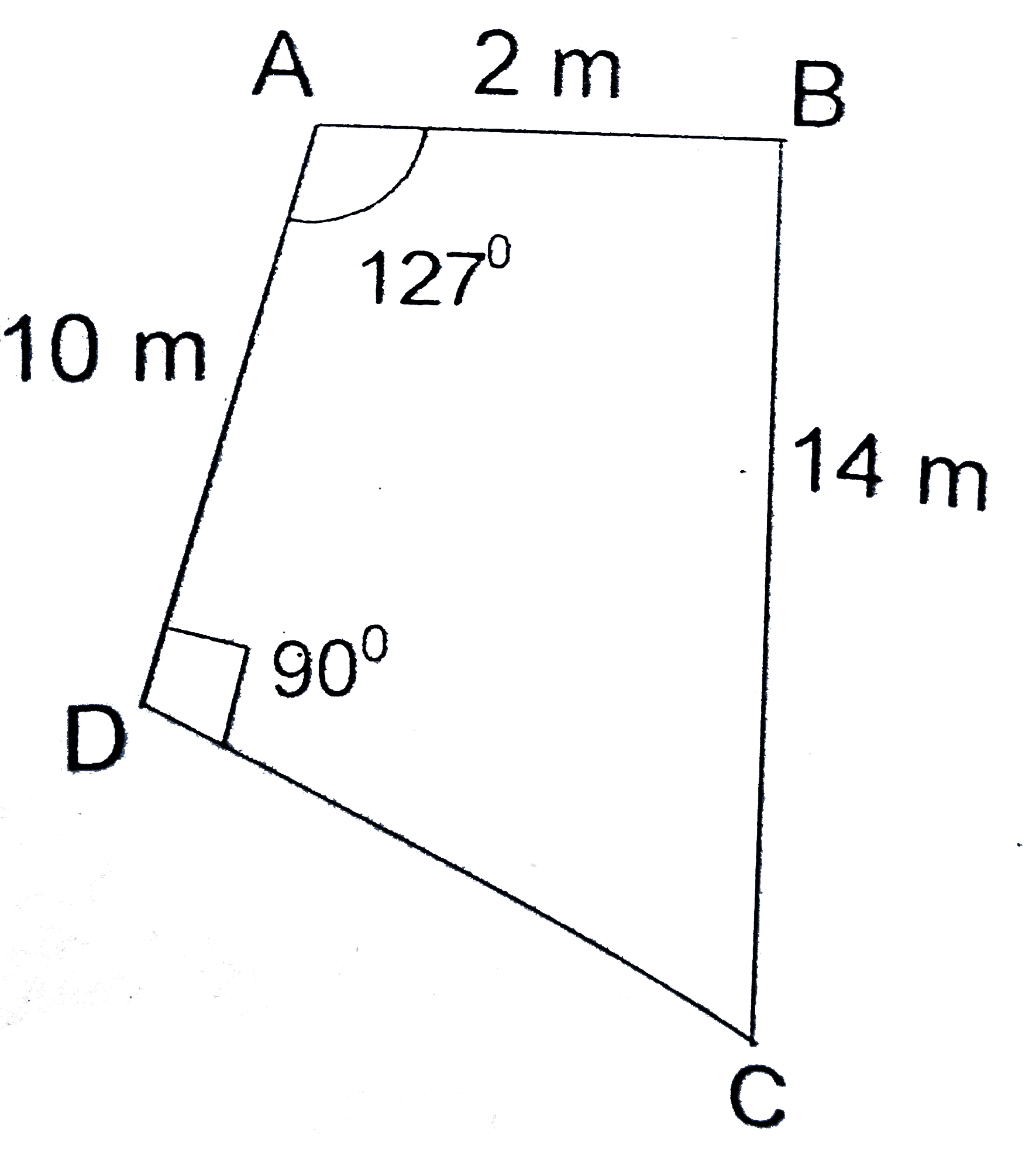A $256 k g m^{2}$
B $512 k g m^{2}$
C $200 k g m^{2}$
D $100 k g m^{2}$

CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Comprehension

Home
Ask Doubt
Profile

The correct Answer is:B

In the present case d=L4 I=ML212+M(L4)2=748ML2 So time period of the physical pendulum is T=2π√IMgd =2π  ⎷748ML2Mg×L4=π√7L3g

Topper's Solved these Questions

Similar Questions

Knowledge Check

In the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is

CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Comprehension

In the present case $d = \frac{L}{4}$
$I = \frac{M L^{2}}{12} + M {(\frac{L}{4})}^{2} = \frac{7}{48} M L^{2}$
So time period of the physical pendulum is $T = 2 π \sqrt{\frac{I}{M g d}}$
$= 2 π \sqrt{\frac{\frac{7}{48 M L^{2}}}{M g \times \frac{L}{4}}} = π \sqrt{\frac{7 L}{3 g}}$

In the figure shown ABCD is a lamina of mass $12 k g$ . The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is