The magnetic field at the point of intersection of diagonals of a square wire loop of side L, carrying a current I is
μ0IπL
2μ0IπL
√2μ0IπL
2√2μ0IπL
The correct Answer is:D
To find the magnetic field at the point of intersection of the diagonals of a square wire loop of side length L carrying a current I, we can follow these steps:
Step 1: Understanding the Geometry
Consider a square wire loop with side length L. The diagonals of the square intersect at the center of the square. The distance from the center to any side of the square is L2.
Step 2: Magnetic Field Contribution from One Side
The magnetic field B at a distance r from a straight current-carrying wire is given by the formula:
B=μ0I4πr(sinα+sinβ)
where α and β are the angles subtended by the wire at the point where the magnetic field is being calculated.
Step 3: Determine Angles
For a square loop, when considering the center, the angles α and β for each side of the square are both 45∘. Thus:
sin45∘=1√2
Therefore, the contribution to the magnetic field from one side of the square is:
B1=μ0I4π(L2)(sin45∘+sin45∘)=μ0I4π(L2)(1√2+1√2)
This simplifies to:
B1=μ0I4π(L2)(2√2)=μ0I4π(L2)⋅√2
Step 4: Calculate the Magnetic Field Contribution
Substituting r=L2:
B1=μ0I√24π(L2)=μ0I√22πL
Step 5: Total Magnetic Field Contribution
Since there are four sides of the square loop, and each contributes equally to the magnetic field at the center, the total magnetic field Bnet is:
Bnet=4×B1=4×μ0I√22πL=2√2μ0IπL
Conclusion
Thus, the magnetic field at the point of intersection of the diagonals of the square wire loop is:
Bnet=2√2μ0IπL
Final Answer
The magnetic field at the point of intersection of diagonals of a square wire loop of side L, carrying a current I is:
2√2μ0IπL
Consider a square wire loop with side length L. The diagonals of the square intersect at the center of the square. The distance from the center to any side of the square is L2.
The magnetic field B at a distance r from a straight current-carrying wire is given by the formula:
B=μ0I4πr(sinα+sinβ)
where α and β are the angles subtended by the wire at the point where the magnetic field is being calculated.
For a square loop, when considering the center, the angles α and β for each side of the square are both 45∘. Thus:
sin45∘=1√2
Therefore, the contribution to the magnetic field from one side of the square is:
B1=μ0I4π(L2)(sin45∘+sin45∘)=μ0I4π(L2)(1√2+1√2)
This simplifies to:
B1=μ0I4π(L2)(2√2)=μ0I4π(L2)⋅√2
Substituting r=L2:
B1=μ0I√24π(L2)=μ0I√22πL
Since there are four sides of the square loop, and each contributes equally to the magnetic field at the center, the total magnetic field Bnet is:
Bnet=4×B1=4×μ0I√22πL=2√2μ0IπL
Thus, the magnetic field at the point of intersection of the diagonals of the square wire loop is:
Bnet=2√2μ0IπL
The magnetic field at the point of intersection of diagonals of a square wire loop of side L, carrying a current I is:
2√2μ0IπL
Similar Questions
Knowledge Check
- Question 1 - Select One
Magnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
A(BA)2μ0πBBA√Aμ0CBA√Aμ0πD2BA√Aμ0√π
The magnetic field at centre of a hexagonal coil of side l carrying a current I is
 View Solution
View SolutionThe magnetic field strength at a point P distant r due to an infinite straight wire carrying a current i is as shown in the figure
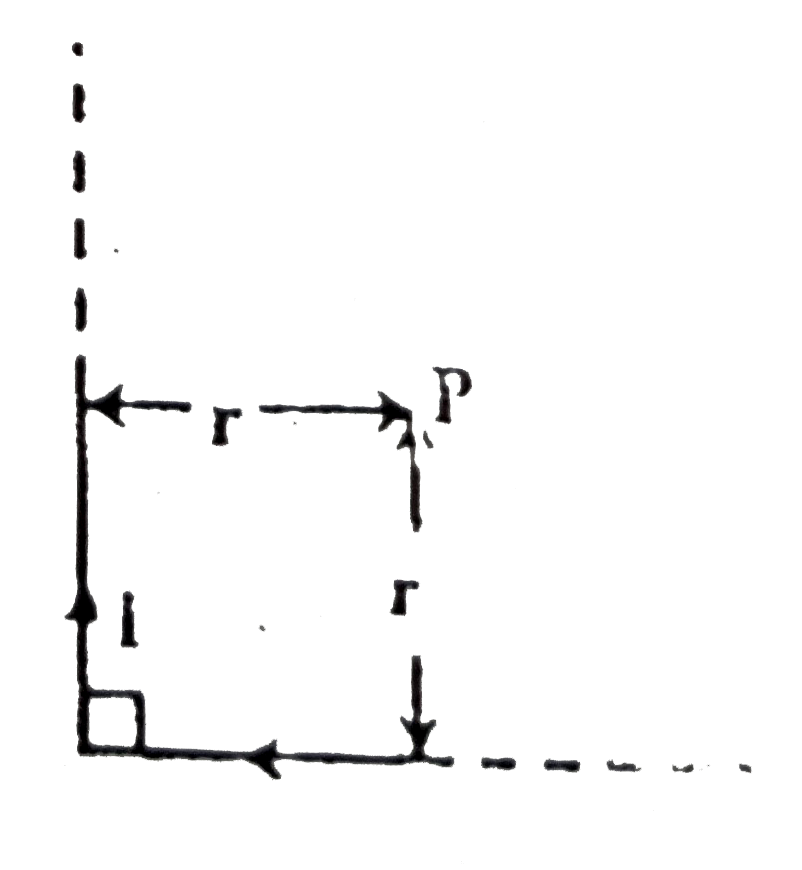 View Solution
View SolutionThe magnetic induction at the point O, if the wire carries a current I, is
 View Solution
View SolutionMagnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionFour long, straight wires, each carrying a current of 5.0 A, are placed in a plane as shown in figure . The points of intersection form a square of side 5.0 cm. (a) Find the magnetic field at the centre P of the square. (b) Q1,Q2,Q3andQ4 are points situated on the diagonals of the square and at a distance from P that is equal to the length of the diagonal of the square. Find the magnetic fields at these points.
 View Solution
View SolutionMagnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
View Solution

