If current I passes through a square-shaped conducting loop of side a, what is the value of the magnetic field at the point of intersection of its two diagonals ?Solution in Bengali
Distacne of the point of intersection of the two diagonals, (O) from each arm of the square [Fig 1.88]. Is r=a2.
For two extreme point of each side, angle subtended at O, θ1=θ2=45∘
So, magnetic field at O due to current I through each arm,
B=μ04π⋅Ir(sinθ1+sinθ2)
=μ04π⋅Ia2(sin45∘+sin45∘)
=μ04π⋅2Ia⋅2×1√2=μ04π2√2Ia
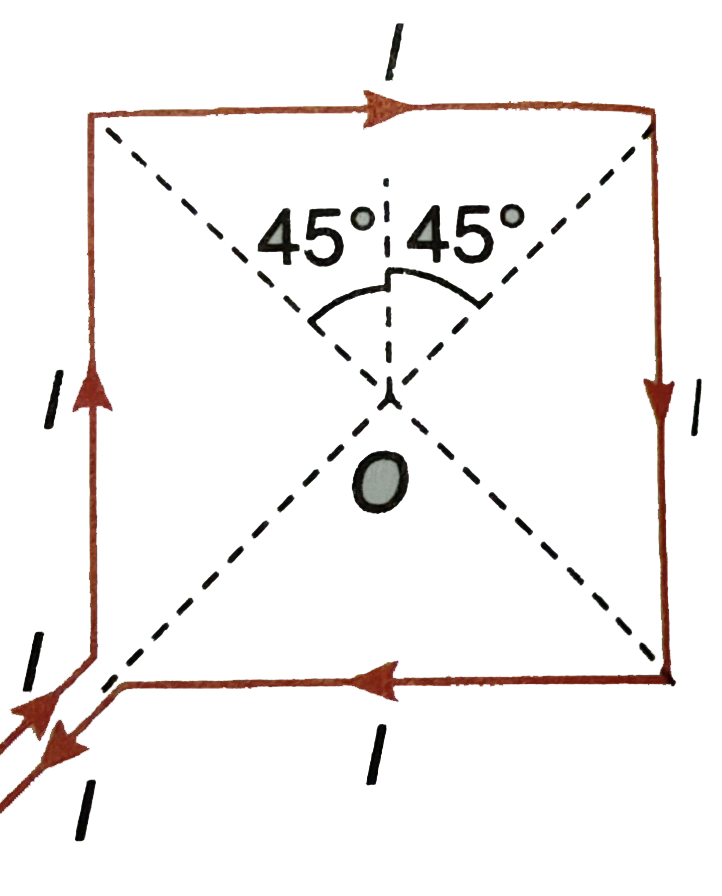
The direction of the magnetic field at the point O due to current I in each arm is the same.
Hene the resultant magnetic field at the point O
=4B=μ04π⋅8√2Ia
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - NCERT TEXTBOOK QUESTIONS WITH ANSWER HINT25videos
ELECTROMAGNETISM
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - NCERT EXAMPLAR QUESTIONS WITH ANSWER HINT (MCQ-1)2videos
ELECTROMAGNETISM
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - SECTION RELATED QUESTIONS64videos
ELECTROMAGNETISM
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CBSE SCANNER17videos
ELECTROMAGNETIC WAVES
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELEMENTARY PHENOMENA OF ELECTROSTATICS EXERCISE - EXAMINATION ARCHIVE2videos
ELEMENTARY PHENOMENA OF ELECTROSTATICS
Similar Questions
Two moving coils meters M1andM2 have the following particulars :
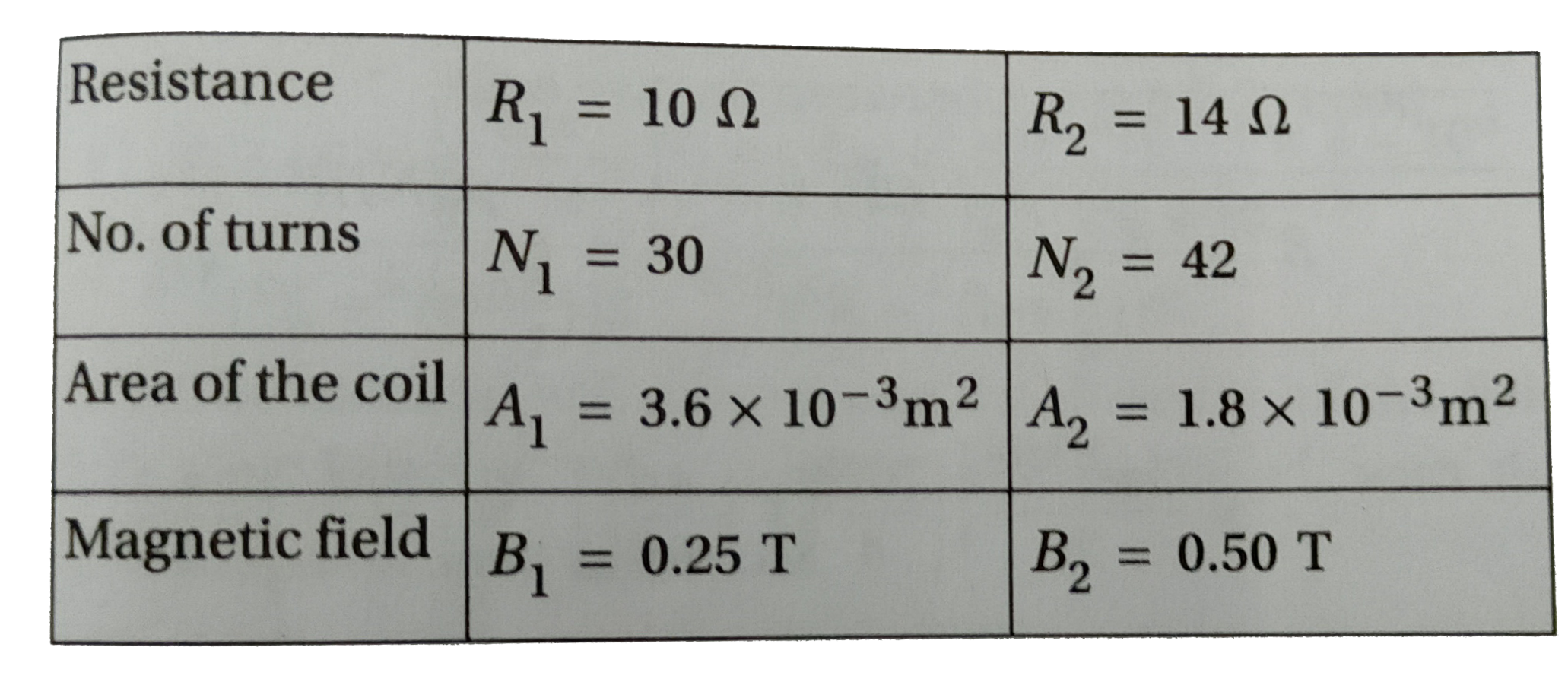
(The spring constancs are identical for the two meters ).02:44View SolutionTwo charged particles traverses indentical helical paths in a completely opposite sense in a uniform magnetic field, →B=B0ˆK.
03:45View SolutionWhat are the fundamental properties of a magnet ?
09:14View SolutionWhat are the directions of electric and magnetic field vectors relative to each other and relative to the direction of propagation of electromagnetic waves?
09:28View SolutionDefine surface density of electric charge
10:16View SolutionA square loop of side a carris a current I . The magnetic field at the centre of the loop is
05:11View SolutionThe magnetic field at the point of intersection of diagonals of a square wire loop of side L, carrying a current I is
02:56View Solutionकिसी वर्गाकार धारा लूप से I धारा प्रवाहित हो, तो उसके केंद्र पर चुंबकीय क्षेत्र का परिमाण ज्ञात करे। वर्ग की प्रत्येक भुजा की लंबाई a है।
05:38View SolutionIf the current through a conducting loop in the shape of an equilaterla triangle of side a be I, what will be the magnitude of the magnetic field of intersection of the three medians ?
03:37View SolutionDue to flow of current I through a square shaped conducting loop, magnetic field generated at its centre is B. the magnetic field generated at the centre of a circular conducting loop having the same perimeter as that of the square and for the flow of the same current is B'. determine the ratio of B to B'.
View SolutionFind the magnetic field at the point of intersection of the diagonals of a square having sides a and carrying current I.
View SolutionThe magnetic field at the point of intersection of diagonals of a square wire loop of side L carrying a current I is
05:00View SolutionThe magnetic field at the point of intersection of diagonals of a square wire loop of side L carrying a current I is
02:14View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
04:00View SolutionA closed circuit is formed in the shape of a square having each side a. If the current in the circuit is Ias shown in figure below, then the direction of the magnetic field at the intersection of the diagonals of the square is
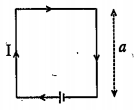 View Solution
View Solution

