Infinite springs with force constantk , 2k, 4k and 8 k .... respectively are connected in series. The effective force constant of the spring will b
2k
k
k2
k4
The correct Answer is:C
To solve the problem of finding the effective force constant of an infinite series of springs with force constants k,2k,4k,8k,…, we will follow these steps:
Step 1: Understand the Series Connection of Springs
When springs are connected in series, the effective spring constant keq can be found using the formula:
1keq=1k1+1k2+1k3+…
In this case, the springs have force constants k,2k,4k,8k,….
Step 2: Write Down the Individual Spring Constants
The individual spring constants are:
- k1=k
- k2=2k
- k3=4k
- k4=8k
- and so on.
Step 3: Set Up the Equation for the Effective Spring Constant
Substituting the values into the formula:
1keq=1k+12k+14k+18k+…
Step 4: Factor Out 1k
We can factor out 1k from the equation:
1keq=1k(1+12+14+18+…)
Step 5: Identify the Series
The series inside the parentheses is a geometric series where:
- The first term a=1
- The common ratio r=12
Step 6: Calculate the Sum of the Infinite Series
The sum S of an infinite geometric series can be calculated using the formula:
S=a1−r
Substituting the values:
S=11−12=112=2
Step 7: Substitute Back to Find keq
Now substituting back into the equation for 1keq:
1keq=1k⋅2
Thus,
keq=k2
Conclusion
The effective force constant of the infinite series of springs is:
k2
When springs are connected in series, the effective spring constant keq can be found using the formula:
1keq=1k1+1k2+1k3+…
In this case, the springs have force constants k,2k,4k,8k,….
The individual spring constants are:
- k1=k
- k2=2k
- k3=4k
- k4=8k
- and so on.
Substituting the values into the formula:
1keq=1k+12k+14k+18k+…
We can factor out 1k from the equation:
1keq=1k(1+12+14+18+…)
The series inside the parentheses is a geometric series where:
- The first term a=1
- The common ratio r=12
The sum S of an infinite geometric series can be calculated using the formula:
S=a1−r
Substituting the values:
S=11−12=112=2
Now substituting back into the equation for 1keq:
1keq=1k⋅2
Thus,
keq=k2
The effective force constant of the infinite series of springs is:
k2
Similar Questions
Infinite springs with force constants k,2k, 4k and 8k … respectively are connected in series. What will be the effective force constant of springs, when k=10N/m
View SolutionDefine spring constant or force constant.
View SolutionTwo springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
View SolutionTwo springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
View SolutionA spring of force constant k is cut into lengths of ratio 1:2:3. They are connected in series and the new force constant is k'. Then they are connected in parallel and force constant is k'. Then k' : k" is :
View SolutionA spring of force constant k. is cut into lengths of ratio 1:2:3. They are connected in series and the new force constant is k'. Then they are connected in parallel and force constant is k''. Then K':K'' is
View SolutionForce constant of a spring (k) is anonymous to
View SolutionFour massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass M kept on a frictionless plane (as shown in figure). If the mass M is displaced in the horizontal direction.

View SolutionA 5 kg block in connected with two spring A and B having force constant, K1=200Nm and K2=300Nm respectively as shown in the figure . The block is released from rest with both the springs in natural length. The maximum energy stored in the spring A will be
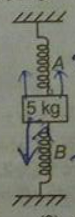
View SolutionA block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
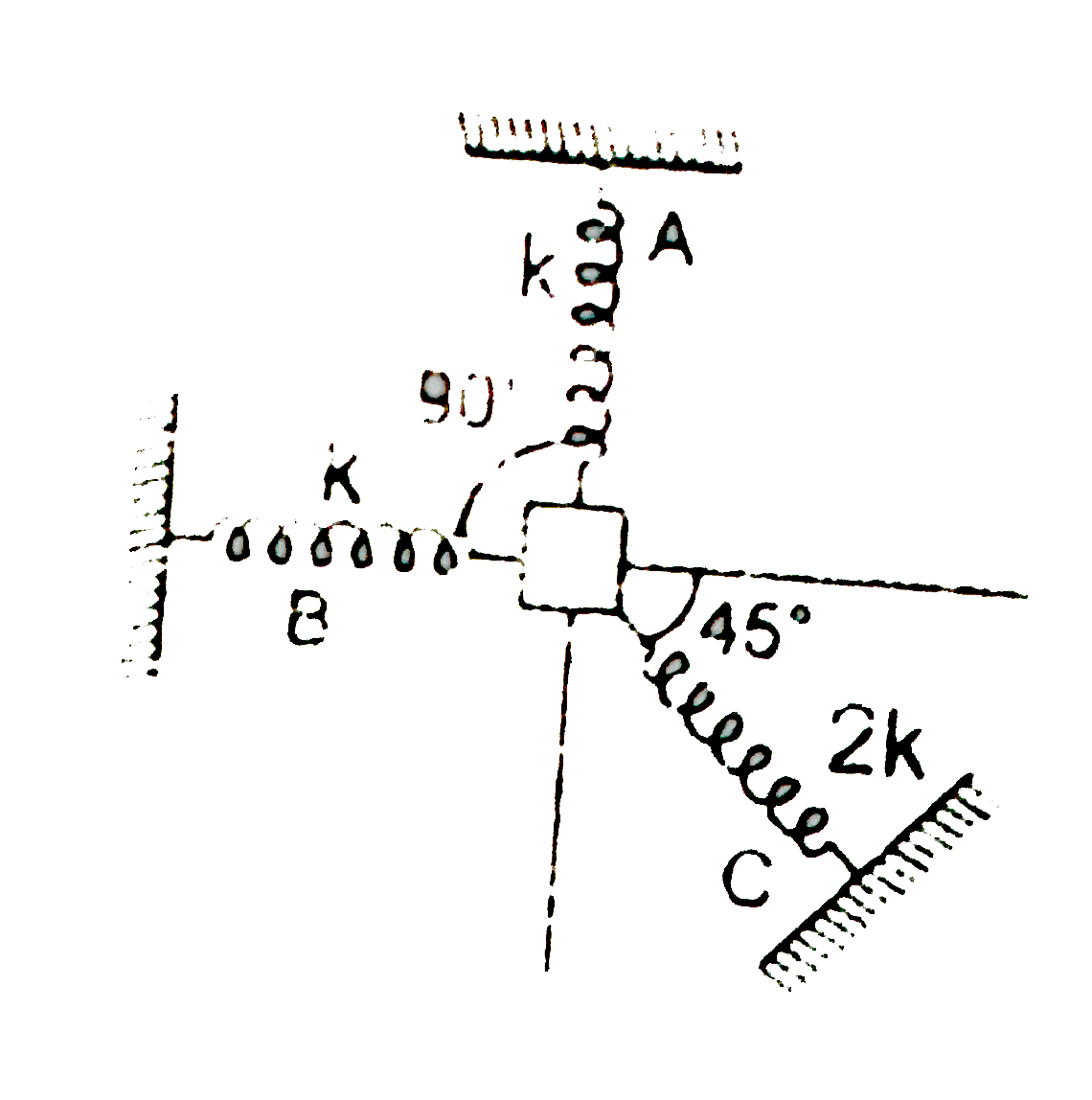
View Solution