Suppose that gold is being plated on to another metal in an electrolytic cell. The half - cell reaction producing the Au(s) is AuCl−4+3e−+Au(s)+4Cl−. If a 0.30 A current runs for 15.00 minute, what mass of Au(s) will be plated, assume all the electrons are used in the reduction of AuCl−4 ? the Faraday constant is 96485 C/mol and molar mass of Au is 197.
0.184 g
0.551 g
1.84 g
0.613 g
The correct Answer is:A
To solve the problem of calculating the mass of gold (Au) plated in an electrolytic cell, we will follow these steps:
Step 1: Convert the time from minutes to seconds
Given:
- Time = 15.00 minutes
To convert minutes to seconds:
Time in seconds=15minutes×60seconds/minute=900seconds
Step 2: Calculate the total charge (Q) passed through the cell
Using the formula:
Q=I×t
Where:
- I=0.30A
- t=900s
Calculating the total charge:
Q=0.30A×900s=270C
Step 3: Calculate the number of moles of electrons transferred
Using Faraday's constant:
Number of moles of electrons=QF
Where:
- F=96485C/mol
Calculating the moles of electrons:
Number of moles of electrons=270C96485C/mol≈0.00280mol
Step 4: Relate moles of electrons to moles of gold plated
From the half-cell reaction:
AuCl−4+3e−→Au(s)+4Cl−
This indicates that 3 moles of electrons are needed to plate 1 mole of gold.
Calculating moles of gold plated:
Moles of Au=Moles of electrons3=0.00280mol3≈0.000933mol
Step 5: Calculate the mass of gold plated
Using the formula:
Mass=Number of moles×Molar mass
Where the molar mass of gold (Au) is given as 197 g/mol.
Calculating the mass of gold:
Mass of Au=0.000933mol×197g/mol≈0.184g
Final Answer
The mass of gold plated is approximately 0.184 g.
---
Given:
- Time = 15.00 minutes
Time in seconds=15minutes×60seconds/minute=900seconds
Using the formula:
Q=I×t
Where:
- I=0.30A
- t=900s
Q=0.30A×900s=270C
Using Faraday's constant:
Number of moles of electrons=QF
Where:
- F=96485C/mol
Number of moles of electrons=270C96485C/mol≈0.00280mol
From the half-cell reaction:
AuCl−4+3e−→Au(s)+4Cl−
This indicates that 3 moles of electrons are needed to plate 1 mole of gold.
Moles of Au=Moles of electrons3=0.00280mol3≈0.000933mol
Using the formula:
Mass=Number of moles×Molar mass
Where the molar mass of gold (Au) is given as 197 g/mol.
Mass of Au=0.000933mol×197g/mol≈0.184g
The mass of gold plated is approximately 0.184 g.
Similar Questions
Suppose that gold is being plated onto another metal in a electrolytic cell. The half− cell reaction producing the Au(s) is AuClc−4→Au(s)+4Clc−+3e−
If a 0.30−A current runs for 1.50min , what mass of Au(s) will be plated, assuming all the electrons are used in the reduction of AuCl4?
View SolutionSuppose that gold is being plated onto another metal in a electrolytic cell. The half− cell reaction producing the Au(s) is AuClc−4→Au(s)+4Clc−+3e−
If a 0.30−A current runs for 1.50min , what mass of Au(s) will be plated, assuming all the electrons are used in the reduction of AuCl4?
View SolutionSuppose that gold is being plated onto another metal in a electrolytic cell. The half− cell reaction producing the Au(s) is AuClc−4→Au(s)+4Clc−+3e−
If a 0.30−A current runs for 15min , what mass of Au(s) will be plated, assuming all the electrons are used in the reduction of AuCl4?
View SolutionTwo metallic plate A and B , each of area 5×10−4m2, are placed parallel to each at a separation of 1cm plate B carries a positive charge of 33.7×10−12C A monocharonatic beam of light , with photoes of energy 5eV each , starts falling on plate A at t=0 so that 1016 photons fall on it per square meter per second. Assume that one photoelectron is emitted for every 106 incident photons fall on it per square meter per second. Also assume that all the emitted photoelectrons are collected by plate B and the work function of plate A remain constant at the value 2eV Determine
(a) the number of photoelectrons emitted up to i=10s,
(b) the magnitude of the electron field between the plate A and B at i=10s,and
(c ) the kinetic energy of the most energotic photoelectrons emitted at i=10s whenit reaches plate B
Negilect the time taken by the photoelectrons to reach plate B Take ε0=8.85×10−12C2N−m2
View Solution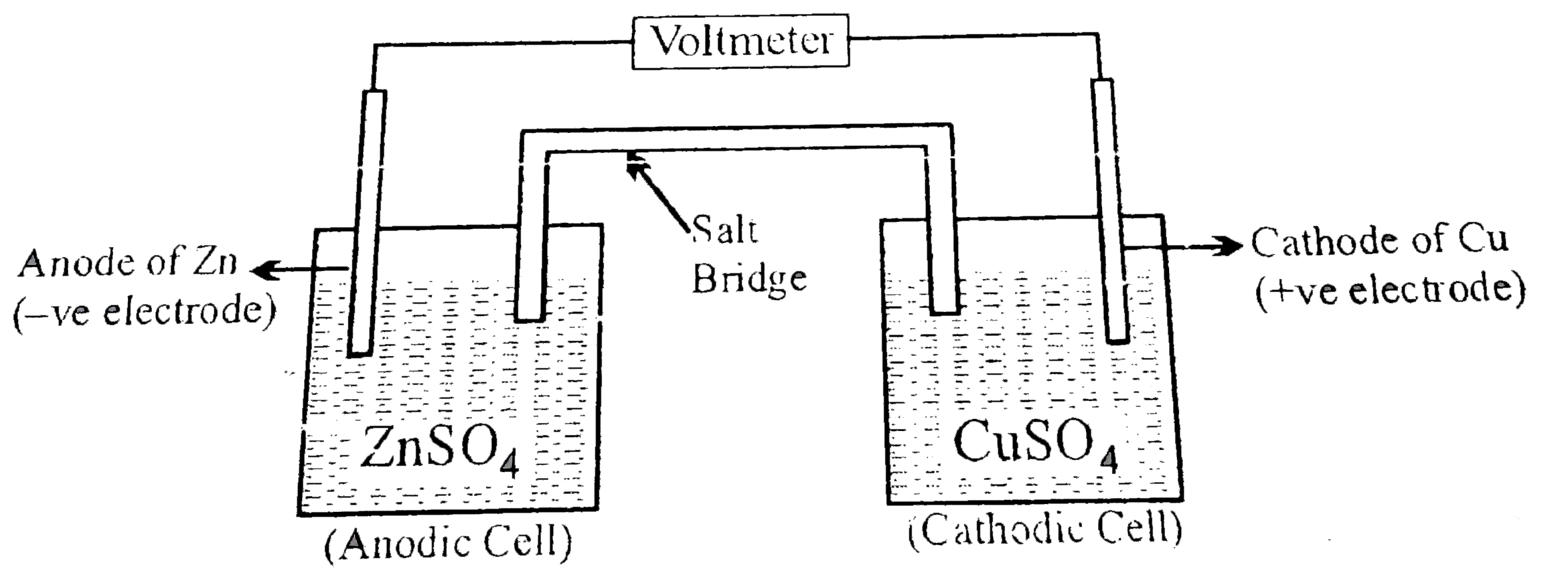
The most pupular electrochemical cell, daniel cell was originally developed by the English chemist john F daniel the general assembly of the cell is as given below An undergraduate student made a Daniel cell using 100cm3 of 0.100MCuSO4 ad 0.100M ZnSO4 solution respectively. The two compartments are connected by suitable salt bridge.
[given E∘(Cu2+/Cu)=0.34V,E(Zn2+/Zn)=−0.76V,2.30RTF=0.06,log2=0.3]
Q. A labmate of the student asked her for some solid CuCl2. while she was lifting the bottle from a shelf, the lid of the bottle slipped and some amount of CuCl2 fell in the CuSO4 compartment at constant volume. She measured the emf of the cell again and found that it has increase by 9 mV. She used this data to calculate the amount of CuCl2 that had spilled in the compartment. Calculate the mass of CuCl2 that had spilled into the daniel cell? (molar mass of CuCl2=135gmol)
View SolutionThe reaction 2AX(g)+2B2(g)→A2(g)+2B2X(g) has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. 2AX⇔A2X2 (fast and reverse)
II. A2X2+B2→A2X+B2X
III. A2X+B2→A2+B2X
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
Let the equilibrium constant of Step I be 2×10−3mol−1L and the rate constants for the formation of A2X and A2 in Step II and III are 3.0×10−2mol−1L−1min and 1×103mol−1L−1min (all data at 25∘C), then what is the overall rate constant (mol−2L2−1min) of the consumption of B2?
View Solution
When a sound wave enters the ear, it sets the eardrum into oscillation, which in turn causes oscillation of 3 tiny bones in the middle ear called ossicles. This oscillation is finally transmitted to the fluid filled in inner portion of the ear termed as inner ear, the motion of the fluid disturbs hair cells within the inner ear which transmit nerve impulses to the brain with the information that a sound is present. The theree bones present in the middle ear are named as hammer, anvil and stirrup. Out of these the stirrup is the smallest one and this only connects the middle ear to inner ear as shown in the figure below. The area of stirrup and its extent of connection with the inner ear limits the sensitivity of the human ear consider a person's ear whose moving part of the eardrum has an area of about 50mm2 and the area of stirrup is about 5mm2. The mass of ossicles is negligible. As a result, force exerted by sound wave in air on eardum and ossicles is same as the force exerted by ossicles on the inner ear. Consider a sound wave having maximum pressure fluctuation of 4×10−2Pa from its normal equilibrium pressure value which is equal to 105Pa. Frequency of sound wave in air is 332ms. Velocity of sound wave in fluid (present in inner ear) is 1500ms. Bulk modulus of air is 1.42×105Pa. Bulk modulus of fluid is 2.18×109Pa.
Q. If the person is using an hearing aid, which increase the sound intensity level by 30 dB, then by what factor the intensity of given sound wave change as perceived by inner ear?
View SolutionA fuel cell is a cell that is continously supplied with an oxidant and a reductant so that if can deliver a current indefinitely.
Fuel cells offer the possibility of achieving high thermodynamic efficiency in the conversion of Gibbs energy into mechanical work.Internal combustion engines at best convert only the fraction (T2−T1)/T2 of the heat of combustion into mechanical work.
While the thermodynamic efficiency of the fuel cell is given by, η=ΔGΔH, where ΔG is the Gibbs energy change for the cell reaction and ΔH is the enthalpy change of the cell reaction.A hydrogen-oxygen fuel cell may have an acidic or alkaline electrolyte.
Pt|H2(g)|H+(aq.)||H2O(l)|O2(g)|Pt,2.303RTF=0.06
The above fuel cell is used to produce constant current supply under constant temperature & 30 atm constant total pressure conditions in a cylinder.If 10 moles H2 and 5 moles of O2 were taken initially.
Rate of consumption of O2 is 10 milli moles per minute. The half-cell reactions are
12O2(g)+2H+(aq)+2e−→H2O(l)E∘=1.246V
2H+(aq)+2e−→H2(g)E∘=0
To maximize the power per unit mass of an electrochemical cell, the electronic and electrolytic resistances of the cell must be minimized.Since fused salts have lower electolytic resistances than aqueous solutions, high-temperature electrochemical cells are of special interest for practical applications.
Calculate e.m.f of the given cell at t=0.(log 2=0.3)
View SolutionAn electron is shot into one end of a solenoid.As it enters the uniform magnetic field within the solenoid, its speed is 800m/s and its velocity vector makes an angle of 30∘ with the central axis of the solenoid. The solenoid carries 4.0A current and has 8000 turn along its length.Find number of revolutions made by the electron within the solenoid by the time it emerges from the solenoid's opposite end. (Use charge of mass ratio em for electron =√3×1011C/kg)Fill your answer in multiple of 103 (neglect end effect)
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
If an object of mass 2 kg and constant b=4N−sm has terminal speed vT in a liquid then time required to reach 0.63vT from start of the motion is :
View Solution
