The reaction 2AX(g)+2B2(g)→A2(g)+2B2X(g) has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. 2AX⇔A2X2 (fast and reverse)
II. A2X2+B2→A2X+B2X
III. A2X+B2→A2+B2X
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
Let the equilibrium constant of Step I be 2×10−3mol−1L and the rate constants for the formation of A2X and A2 in Step II and III are 3.0×10−2mol−1L−1min and 1×103mol−1L−1min (all data at 25∘C), then what is the overall rate constant (mol−2L2−1min) of the consumption of B2?
6×10−5
1.2×10−4
3×10−5
1.5×10−5
The correct Answer is:B
To solve the problem, we need to derive the overall rate constant for the consumption of B2 based on the given reaction mechanism and the provided equilibrium constant and rate constants. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Rate-Determining Step (RDS)
The slowest step in the given mechanism is the second step:
A2X2+B2→A2X+B2X
This step will determine the overall rate of the reaction.
Step 2: Write the Rate Expression for the RDS
The rate of the reaction for the RDS can be expressed as:
Rate=k2(A2X2)(B2)
where k2 is the rate constant for the second step.
Step 3: Express the Concentration of the Intermediate A2X2
Since A2X2 is an intermediate, we need to express its concentration in terms of the reactants using the equilibrium constant from the first step:
2AX⇌A2X2
The equilibrium constant Ke for this step is given by:
Ke=(A2X2)(AX)2
Given that Ke=2×10−3mol−1L, we can rearrange this to find (A2X2):
(A2X2)=Ke(AX)2
Substituting the value of Ke:
(A2X2)=(2×10−3)(AX)2
Step 4: Substitute (A2X2) into the Rate Expression
Now we substitute (A2X2) back into the rate expression:
Rate=k2(2×10−3)(AX)2(B2)
Step 5: Determine the Overall Rate Constant for B2
Since B2 is consumed in the reaction, we need to express the rate in terms of (B2):
The overall rate can be expressed as:
Rate=koverall(AX)2(B2)
Comparing both expressions for the rate, we have:
koverall=k2(2×10−3)
Step 6: Substitute the Value of k2
The rate constant k2 for the second step is given as:
k2=3.0×10−2mol−1L min−1
Now substituting this value:
koverall=(3.0×10−2)(2×10−3)
koverall=6.0×10−5mol−2L2min−1
Step 7: Final Calculation
Thus, the overall rate constant for the consumption of B2 is:
koverall=6.0×10−5mol−2L2min−1
The slowest step in the given mechanism is the second step:
A2X2+B2→A2X+B2X
This step will determine the overall rate of the reaction.
The rate of the reaction for the RDS can be expressed as:
Rate=k2(A2X2)(B2)
where k2 is the rate constant for the second step.
Since A2X2 is an intermediate, we need to express its concentration in terms of the reactants using the equilibrium constant from the first step:
2AX⇌A2X2
The equilibrium constant Ke for this step is given by:
Ke=(A2X2)(AX)2
Given that Ke=2×10−3mol−1L, we can rearrange this to find (A2X2):
(A2X2)=Ke(AX)2
Substituting the value of Ke:
(A2X2)=(2×10−3)(AX)2
Now we substitute (A2X2) back into the rate expression:
Rate=k2(2×10−3)(AX)2(B2)
Since B2 is consumed in the reaction, we need to express the rate in terms of (B2):
The overall rate can be expressed as:
Rate=koverall(AX)2(B2)
Comparing both expressions for the rate, we have:
koverall=k2(2×10−3)
The rate constant k2 for the second step is given as:
k2=3.0×10−2mol−1L min−1
Now substituting this value:
koverall=(3.0×10−2)(2×10−3)
koverall=6.0×10−5mol−2L2min−1
Thus, the overall rate constant for the consumption of B2 is:
koverall=6.0×10−5mol−2L2min−1
Topper's Solved these Questions
- CHEMICAL KINETICSBook:CENGAGE CHEMISTRY ENGLISHChapter:CHEMICAL KINETICSExercise:Exercises Multiple Correct
Explore 33 Videos
- CHEMICAL KINETICSBook:CENGAGE CHEMISTRY ENGLISHChapter:CHEMICAL KINETICSExercise:Exercises Single Correct
Explore 177 Videos
- CHEMICAL KINETICSBook:CENGAGE CHEMISTRY ENGLISHChapter:CHEMICAL KINETICSExercise:Ex4.4 Objective
Explore 10 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBook:CENGAGE CHEMISTRY ENGLISHChapter:CARBOXYLIC ACIDS AND THEIR DERIVATIVESExercise:Exercises Archives (Analytical And Descriptive)
Explore 34 Videos
- COORDINATION COMPOUNDSBook:CENGAGE CHEMISTRY ENGLISHChapter:COORDINATION COMPOUNDSExercise:Archives Subjective
Explore 18 Videos
Similar Questions
The reaction 2AX(g)+2B2(g)→A2(g)+2B2X(g) has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. 2AX⇔A2X2 (fast and reverse)
II. A2X2+B2→A2X+B2X
III. A2X+B2→A2+B2X
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
How many times the rate of formation of A2 will increase if concentrations of AX is doubled and that of B2 is increased theee fold?
View Solution2 is the equilibrium constant for the reaction A2+B2⇔2AB at a given temperature. What is the degree of dissociation for A2 or B2
View Solution
Knowledge Check
The reaction ,2AB(g)+2C(g)→A2(g)+2BC(g) proceeds according to the mechanism .
I. 2AB⇔A2B2 (fast)
II. A2B2+C→A2B+BC (slow )
III. A2B+C→A2+BC (fast)
what will be the initial rate taking [AB] = 0.2 M and [C] = 0.5 M ? The Kc for the step I is 102M−1 and rate constant for the step II is 3.0×10−3mol−1−1minA0.0716M−1minB0.0891M−1minC0.006M−1minD0.0257M−1min
The gaseous reaction A(g)+B(g)⇔2C(g)+D(g)+q kJ is most favoured at :
View SolutionIn a reaction A2(g)+4B2(g)⇔2AB4(g),ΔH<0. The formation of AB4 is not favoured by
View SolutionThe equilibrium constant for the reaction
A2(g)+B2(g)⇔2AB(g)
is 20 at 500K. The equilibrium constant for the reaction 2AB(g)⇔A2(g)+B2(g) would be
View SolutionIf equilibrium constant for the reaction
A2+B2⇔2AB is k, then for the backward reaction AB⇔1/2A2+1/2B2 the equilibrium constant k' is 1/K.
View SolutionThe following pictures represents the equilibrium state for three different reactions of the type
A2+X2⇔2AX (X=B,CorD)
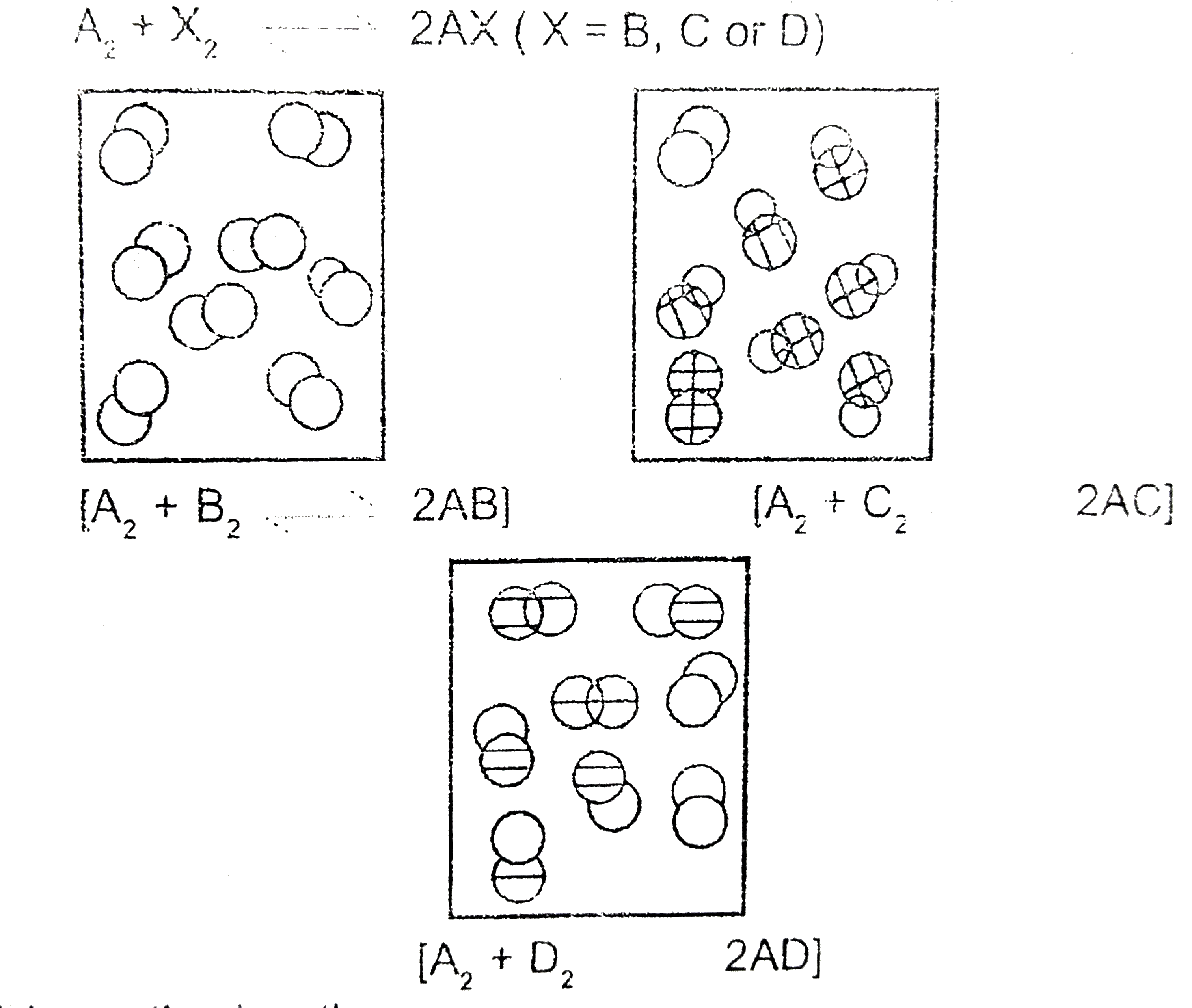
Which reaction has the largest equilibrium constant?
View SolutionMechanism of the reaction is:
A2k⇐⇒k'2A
A+B2k2−−→C+B
B+A2k2−−→C+A
What is−d[A2]dt
View SolutionConisder the reaction mechanism:
A2keq⇐⇒2A(fast) (where A is the intermediate.)
A+B−−→k1P(slow)
The rate law for the reaction is
View Solution
