Using the conservation laws, demonstrate that the total mechanical energy of a planet of mass m moving around the Sun along an ellipse depends only on its semi-major axis a. Find this energy as a function of a.
The correct Answer is:A
To demonstrate that the total mechanical energy of a planet of mass m moving around the Sun along an ellipse depends only on its semi-major axis a, we can use the conservation of mechanical energy in a gravitational field. Here's the step-by-step solution:
Step 1: Define the Total Mechanical Energy
The total mechanical energy E of the planet in orbit is given by the sum of its kinetic energy K and potential energy U:
E=K+U
where the kinetic energy K is given by:
K=12mv2
and the gravitational potential energy U is given by:
U=−GMmr
Here, G is the gravitational constant, M is the mass of the Sun, m is the mass of the planet, and r is the distance from the planet to the Sun.
Step 2: Use the Conservation of Angular Momentum
For a planet in elliptical orbit, the angular momentum L is conserved. The angular momentum is given by:
L=mr2ω
where ω is the angular velocity. Since L is constant, we can express v in terms of r and ω:
v=rω
Step 3: Relate the Semi-Major Axis to the Orbit
In an elliptical orbit, the semi-major axis a is related to the maximum distance r1 (aphelion) and minimum distance r2 (perihelion) as follows:
a=r1+r22
Step 4: Express Kinetic and Potential Energy in Terms of a
Using the vis-viva equation for elliptical orbits, we can express the velocity v at any point in the orbit as:
v2=GM(2r−1a)
Substituting this into the expression for kinetic energy:
K=12m(GM(2r−1a))
Step 5: Substitute into the Total Energy Equation
Now substituting K and U into the total energy equation:
E=12m(GM(2r−1a))−GMmr
Combining the terms:
E=GMm2a−GMmr
Step 6: Simplify the Expression
For an elliptical orbit, the average distance r over one complete orbit can be approximated by the semi-major axis a:
E=−GMm2a
This shows that the total mechanical energy E depends only on the semi-major axis a.
Final Result
Thus, the total mechanical energy of a planet moving in an elliptical orbit around the Sun is given by:
E=−GMm2a
The total mechanical energy E of the planet in orbit is given by the sum of its kinetic energy K and potential energy U:
E=K+U
where the kinetic energy K is given by:
K=12mv2
and the gravitational potential energy U is given by:
U=−GMmr
Here, G is the gravitational constant, M is the mass of the Sun, m is the mass of the planet, and r is the distance from the planet to the Sun.
For a planet in elliptical orbit, the angular momentum L is conserved. The angular momentum is given by:
L=mr2ω
where ω is the angular velocity. Since L is constant, we can express v in terms of r and ω:
v=rω
In an elliptical orbit, the semi-major axis a is related to the maximum distance r1 (aphelion) and minimum distance r2 (perihelion) as follows:
a=r1+r22
Using the vis-viva equation for elliptical orbits, we can express the velocity v at any point in the orbit as:
v2=GM(2r−1a)
Substituting this into the expression for kinetic energy:
K=12m(GM(2r−1a))
Now substituting K and U into the total energy equation:
E=12m(GM(2r−1a))−GMmr
Combining the terms:
E=GMm2a−GMmr
For an elliptical orbit, the average distance r over one complete orbit can be approximated by the semi-major axis a:
E=−GMm2a
This shows that the total mechanical energy E depends only on the semi-major axis a.
Thus, the total mechanical energy of a planet moving in an elliptical orbit around the Sun is given by:
E=−GMm2a
Similar Questions
Kepler's law starts that square of the time period of any planet moving around the sun in an elliptical orbit of semi-major axis (R) is directly proportional to
View SolutionIf the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, its areal velocity is :
View SolutionThe kinetic energy of a particle moving along a circle of radius R depends on the distance covered s as K.E = KS2 where K is a constant. Find the force acting on the particle as a function of S -
View SolutionThe potential energy of particle of mass 1kg moving along the x-axis is given by U(x)=16(x2−2x) J, where x is in meter. Its speed at x=1 m is2m/s. Then,
View SolutionTotal mechanical energy E of an object of mass m, at a height h above the ground is given by the relation
E = mgh +p22m
Find the dimensions of p. (g = acceleration due to gravity).
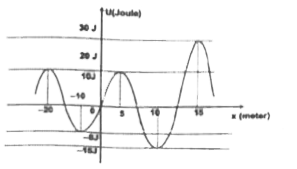
View SolutionThe variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
View SolutionThe potential energy of a particle of mass 1 kg moving along x-axis given by U(x)=[x22−x]J. If total mechanical speed (in m/s):-
View SolutionLength of a year on a planet is the duration in which it completes one revolution around the sun. Assume path of the planet known as orbit to be circular with sun at the centre. The length T of a year of a planet orbiting around the sun in circular orbit depends on universal gravitational constant G, mass ms of the sun and radius r of the orbit. if T∝Gambsrc find value of a+b+2c.
View SolutionThe potential energy of an object of mass m moving in xy plane in a conservative field is given by U = ax + by , where x and y are position coordinates of the object. Find magnitude of its acceleration :-
View SolutionThe kinetic energy of a particle moving along a circle of radius R depends on the distance covered S as K =α.S2, where α is a constant. Find the force acting on the particle as a function of S.
View Solution
