Using the conservation laws, demonstrate that the total mechanical energy of a planet of mass m moving around the Sun along an ellipse depends only on its semi-major axis a. Find this energy as a function of a.
From the previous problem, if r1, r2 are the maximum and minimum distances from the sun to the planet and v1, v2 are the corresponding velocities, then, say,
E=12mv22−γmmsr2
=γmmsr1+r2⋅r1r2−γmmsr2=−γmmsr1+r2=−γmms2a
where 2a= major axis =r1+r2. The same result can also be obtained directly by writing an equation analogous to Eq(1) of problem
E=12m.r2+M22mr2−γmmsr
(Here M is angular momentum of the planet and m is its mass). For position .r=0 and we get the quardratic
Er2+γmmsr−M22m=0
The sum of the two roots of this equation are
r1+r2=−γmmsE=2a
Thus E=−γmms2a=constant
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body56videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Laws Of Conservation Of Energy, Momentum And Angular Momentum82videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
If the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, its areal velocity is :
View SolutionThe total mechanical energy of a 2.00 kg particle moving along an x axis is 5.00 J. The potential energy is given as U(x)=(x4−2.00x2)J, with x in meters. Find the maximum velocity.
View Solution
Knowledge Check
- Question 1 - Select One
A planet of mass m is moving around the sun in an elliptical orbit of semi-major axis a :
AThe total mechanical energy of the planet is varying periodically with timeBThe total energ of the planet is constant and equals −GmMs2a,Ns is mass of sunCTotal mechanical energy of the planet is constant and equals −GmMsa,M2 is mass of sunDDate is insufficient of arrice at a conclusion - Question 2 - Select One
Kepler's law starts that square of the time period of any planet moving around the sun in an elliptical orbit of semi-major axis (R) is directly proportional to
ARB1RCR3D1R3 - Question 3 - Select One
The satellite of mass m is orbiting around the earth in a circular orbit with a velocity v.What will be its total energy ?
A(3/4)mv2B(1/2)mv2Cmv2D(1/2)mv2
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
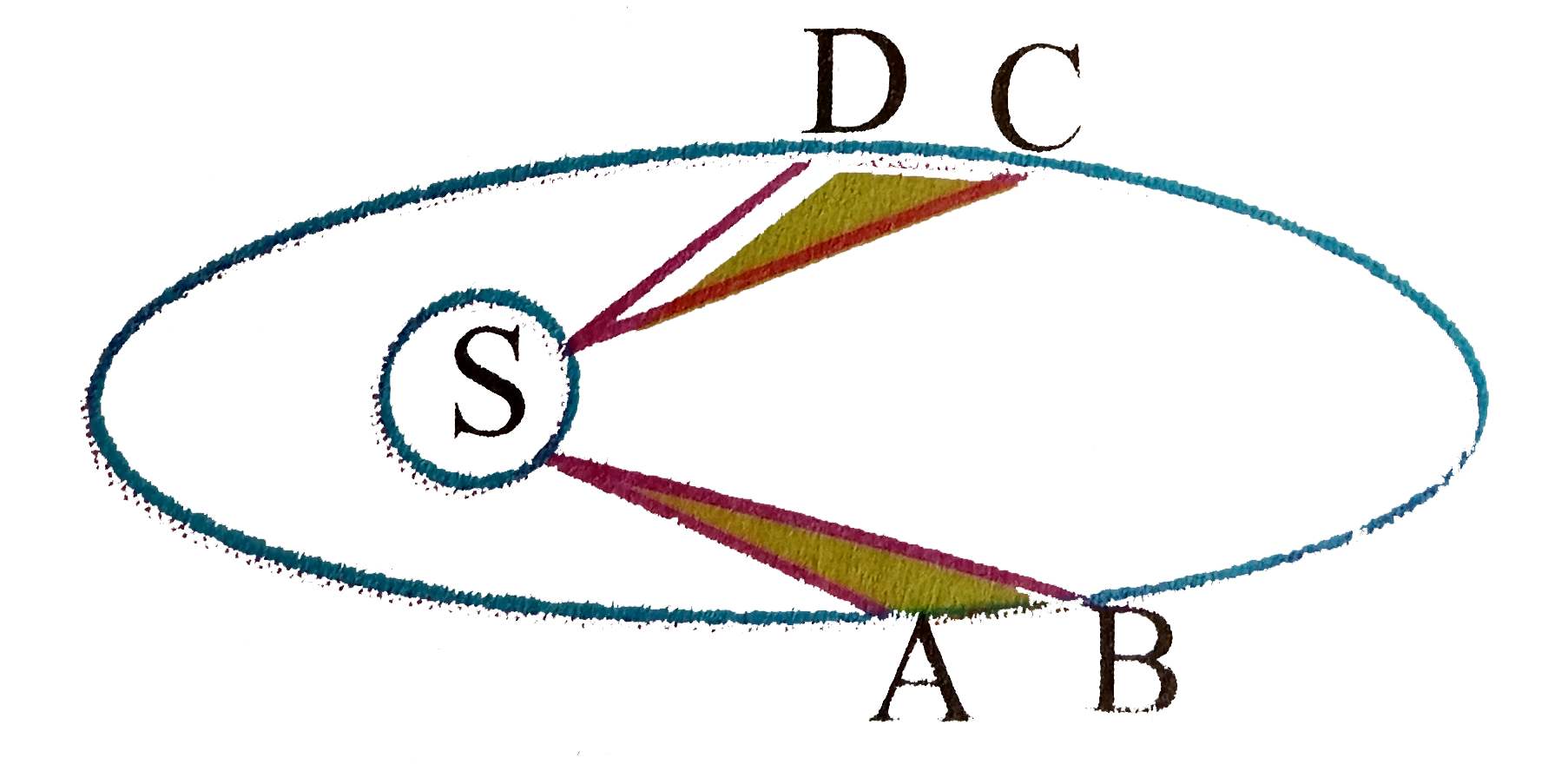 View Solution
View SolutionThe motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
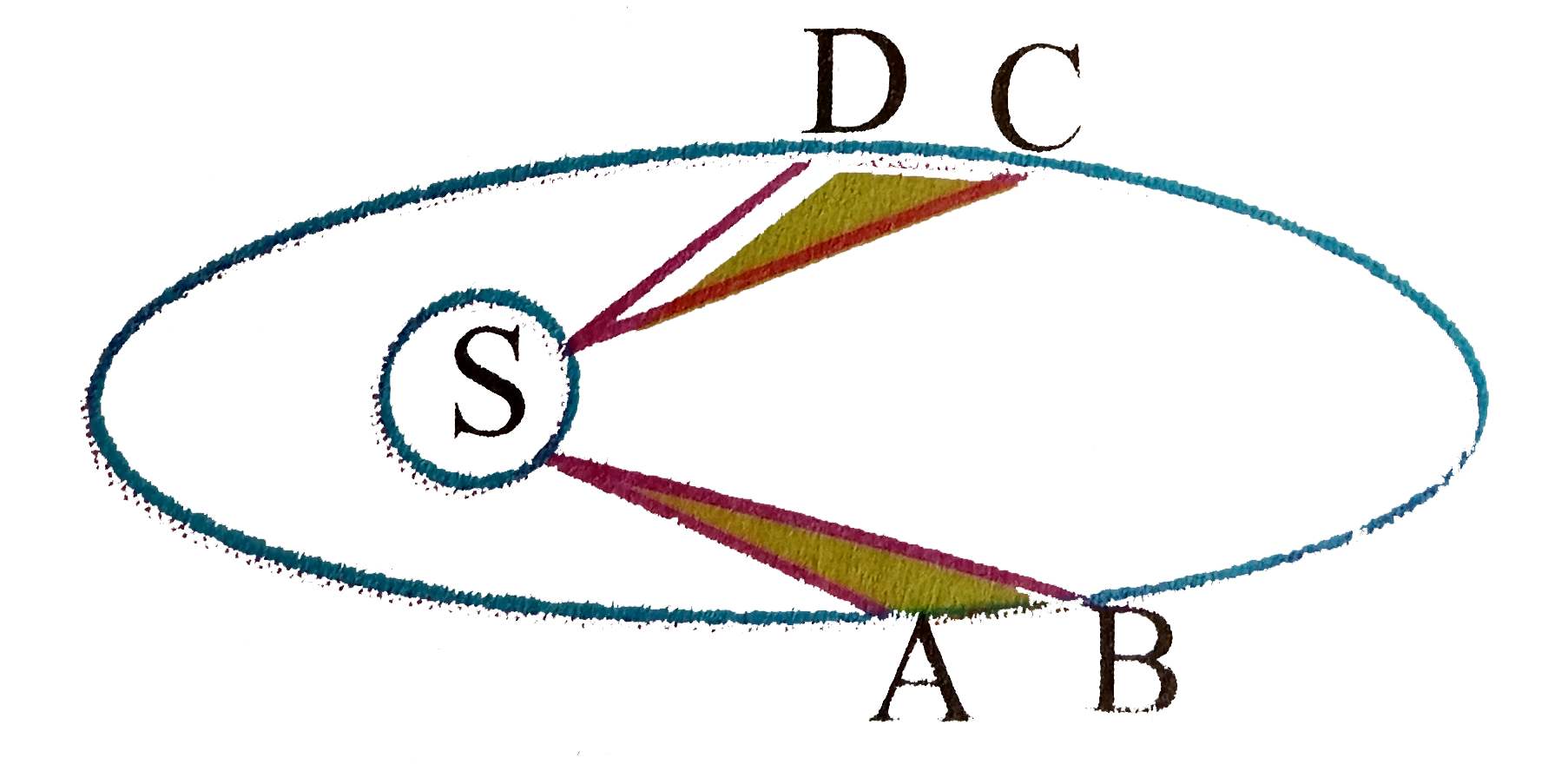 View Solution
View Solution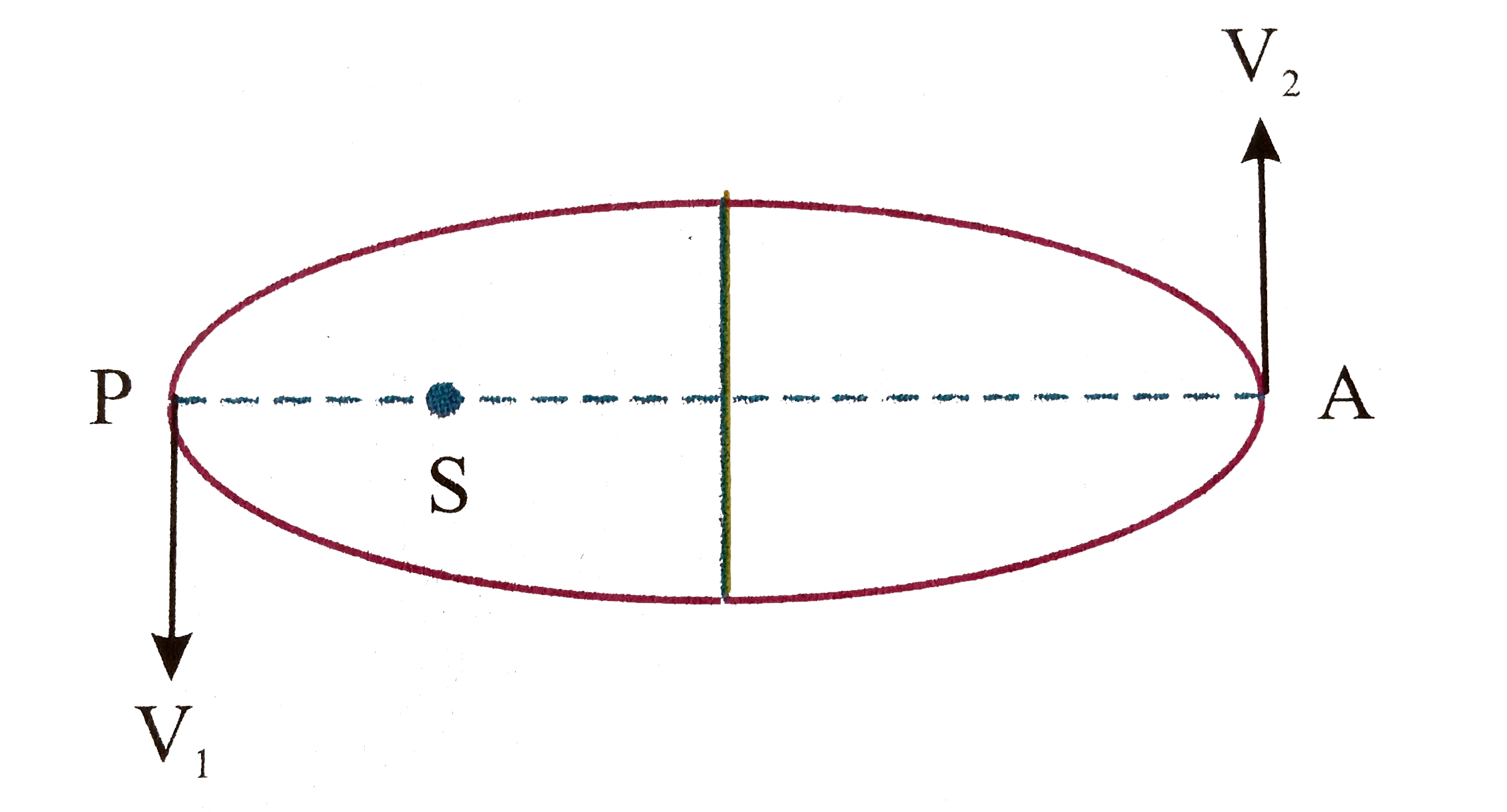
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find total energy of planet interms of given parameters.View SolutionAn artificial moving in a circular orbit around the earth has total mechanical energy E0. Its kinetic energy is
View SolutionThe variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
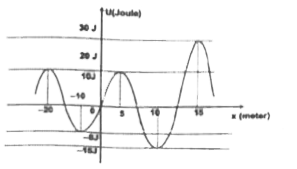 View Solution
View Solution

