Two rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.

Let t∘C=increase in the temperature.
Increase in length of first rod=l1α1t
Increase in length of second rod=l2α2t
Total extension in length due to rise in temperature
=l1α1t+l2α2t=(l1α1+l2α2)t ..(i)
since the walls are rigid, this increase in length will not happen. This will be compensated by equal and opposite forces F, F producing decrease in the lengths of the rods due to elasticity.
Decrease in length of first rod=F×l1Y1×A
And decrease in length of second rod =F×l2Y2×A
Total decrease in length due to elastic force
=FA(l1Y1+l2Y2) ..(ii)
From Eqs. (i) and (ii) we have
FA(l1Y1+l2Y2)=(l1α1+l2α2)t
or F=A(l1α1+l2α2)tl1Y1+l2Y2 ..(iii)
ii. Length of the first rod=original length+increase in length due to temperature − decrease in length due to force
=(l1+l1α1t−FAl1Y1)
and length of second rod=l2+l2α2t−FAl2Y2
The total length is same =l1+l2 at all temperatures.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.123videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.222videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
Two metal rods of the same length and area of cross-section are fixed end to end between rigid supports. The materials of the rods have Young moduli Y1 and Y2 , and coefficient of linear expansion α1 and α2 . The junction between the rod does not shift and the rods are cooled
View SolutionTwo rods of different materials are placed between massive walls as shown in figure. The cross section of the rods is A, their moduil of elastricity are E1 and E2 respectively. If rods are heated by t degrees, then (coefficients of liner expansion of material of rods are α1 and α2 respectively)
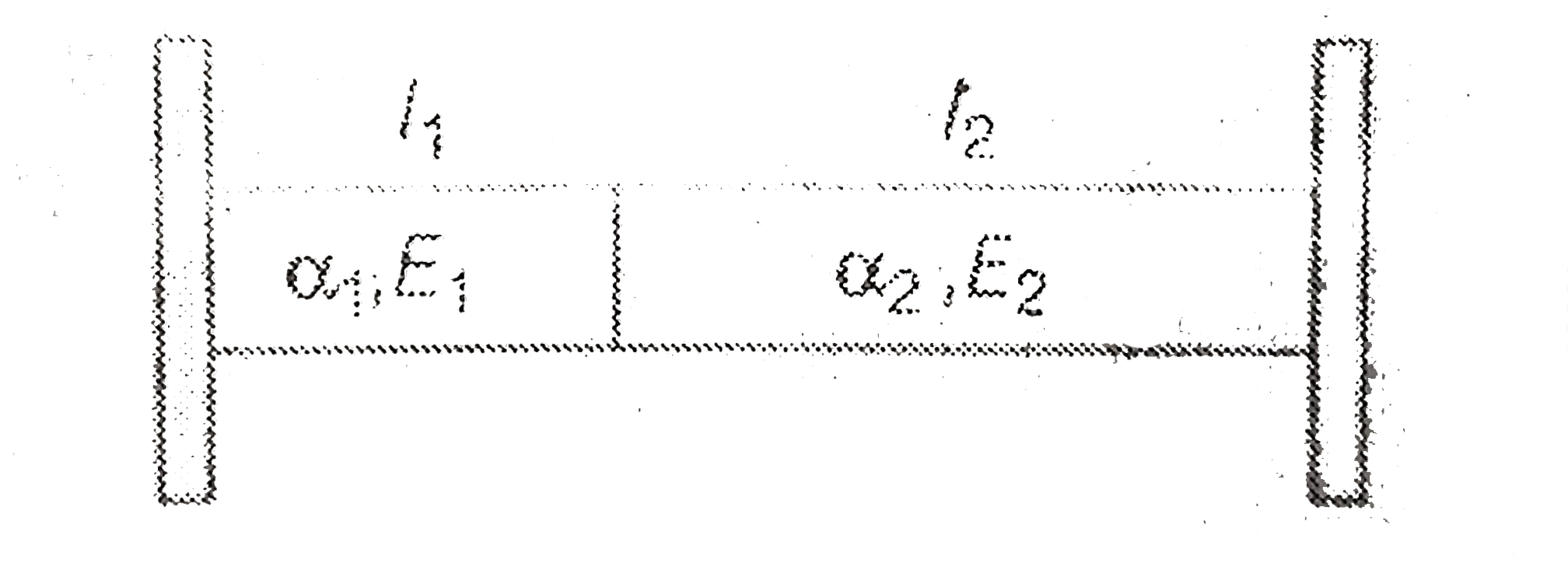 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTα
There are two rods of length l1 and l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.View Solution
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will beView SolutionA uniform rod of length L, has a mass per unit length λ and area of cross section A. The elongation in the rod is l due to its own weight, if it suspended form the celing of a room. The Young's modulus of the rod is
View SolutionTwo metallic rods of length l and 3l have coefficient of linear expansion α and 3α respectively. The coefficient of linear expansion ofr their series combinations, is
View SolutionA rod has variable co-efficient of linear expansion α=x5000. If length of the rod is 1 m . Determine increase in length of the rod in (cm) on increasing temperature of the rod by 100∘C.
_S01_121_Q01.png) View Solution
View SolutionAn isosceles triangles is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is
 View Solution
View SolutionAn isosceles triangles is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is
 View Solution
View Solution

