The co-efficient of thermal expansion of a rod is temperature dependent and is given by the formula α=aT, where a is a positive constant at T in∘C. if the length of the rod is l at temperature 0∘C, then the temperature at which the length will be 2l is
10∘C
20∘C
200∘C
100∘C
The correct Answer is:C
To solve the problem, we need to find the temperature at which the length of the rod will be doubled, given that the coefficient of thermal expansion is temperature dependent and defined as α=aT.
1. Understanding the Problem:
- The initial length of the rod at 0∘C is l.
- We want to find the temperature T at which the length of the rod becomes 2l.
2. Change in Length:
- The increase in length ΔL required to go from l to 2l is:
ΔL=2l−l=l
3. Using the Coefficient of Thermal Expansion:
- The coefficient of thermal expansion is given by:
α=aT
- The formula for the change in length due to thermal expansion is:
ΔL=α⋅l⋅ΔT
- Substituting for α:
ΔL=(aT)⋅l⋅ΔT
4. Setting Up the Equation:
- We know ΔL=l, so we can set up the equation:
l=(aT)⋅l⋅ΔT
- Dividing both sides by l (assuming l≠0):
1=aT⋅ΔT
5. Finding ΔT:
- Rearranging gives:
ΔT=1aT
- Here, ΔT is the change in temperature from 0∘C to T, thus:
ΔT=T−0=T
- Therefore, we have:
T=1aT
6. Multiplying Both Sides by aT:
- This leads to:
aT2=1
7. Solving for T:
- Rearranging gives:
T2=1a
- Taking the square root:
T=√1a
8. Final Result:
- The temperature at which the length of the rod will be 2l is:
T=√2ln2a
Summary of the Solution:
The temperature at which the length of the rod will be 2l is given by:
T=√2ln2a
- The initial length of the rod at 0∘C is l.
- We want to find the temperature T at which the length of the rod becomes 2l.
- The increase in length ΔL required to go from l to 2l is:
ΔL=2l−l=l
- The coefficient of thermal expansion is given by:
α=aT
- The formula for the change in length due to thermal expansion is:
ΔL=α⋅l⋅ΔT
- Substituting for α:
ΔL=(aT)⋅l⋅ΔT
- We know ΔL=l, so we can set up the equation:
l=(aT)⋅l⋅ΔT
- Dividing both sides by l (assuming l≠0):
1=aT⋅ΔT
- Rearranging gives:
ΔT=1aT
- Here, ΔT is the change in temperature from 0∘C to T, thus:
ΔT=T−0=T
- Therefore, we have:
T=1aT
- This leads to:
aT2=1
- Rearranging gives:
T2=1a
- Taking the square root:
T=√1a
- The temperature at which the length of the rod will be 2l is:
T=√2ln2a
The temperature at which the length of the rod will be 2l is given by:
T=√2ln2a
Similar Questions
Coefficient of thermal expansion of a wire varies with temperature T as α=1.6×10−6T, where T is temperature in degree Celsius. If the length of wire is 10 m at0∘C, what is the change in length of wire (in mm), when its temperature is raised to 25∘C?
View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
View SolutionA rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
View SolutionThe temperature gradient in a rod of 0.5m length is 80∘C/m. It the temperature of hotter end of the rod is 30∘C, then the temperature of the cooler end is
View SolutionThe coefficient of linear expansion of a rod of length 1 m, at 27∘C, is varying with temperature as α = 2/T unit (300K≤T≤600K), where T is the temperature of rod in Kelvin. The increment in the length of rod if its temperature increases from 27∘C to 327∘C is
View SolutionThe coefficient of linear expansion 'α' of the material of a rod of length l0 varies with absolute temperature as α=aT−bT2 where a & b are constant. The linear expansion of the rod when heated from T1 to T2=2T1 is :-
View SolutionA rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as k=a/T, where a is a constant. The ends of the rod are kept at temperatures T1andT2. Find the function T(x), where x is the distance from the end whose temperature is T1.
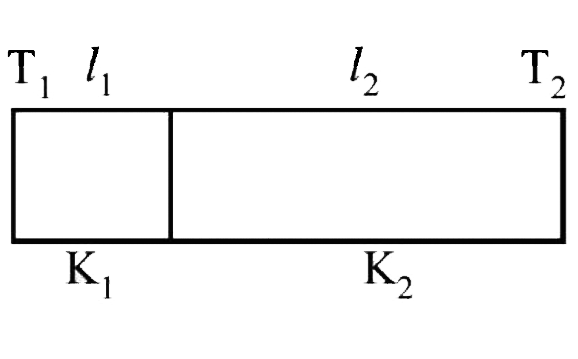
View SolutionOne end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
View SolutionConsider three rods of length L1,L2andL3 espectively joined in series. Each has same cross - sectional area with Young's moduli Y, 2Y and 3Y respectively and thermal coefficients of linear expansion α,2αand3α respectively. They are placed between two rigid fixed walls. The temperature of the whole system is increased and it is found that length of the middle rod does not change with temperature rise. Find the value of 9L1L3.
View SolutionThe natural length of a metallic root at 0∘C is l1 at θ∘C is l2. The given lengths of the rod at θ∘ is l3, then:
View Solution
