The natural length of a metallic root at is at is . The given lengths of the rod at is , then:
The thermal stress in the rod is non zero if
The strain in the rod is zero if
The thermal stress in the rod is non-zero if
The thermal stress and strain will be zero if
The correct Answer is:A, C, D
To solve the problem regarding the lengths of a metallic rod at different temperatures, we can follow these steps:
1. Understand the Problem:
- We have a metallic rod with a natural length l1 at 0∘C.
- The length of the rod at a temperature θ∘C is l2.
- The given length of the rod at temperature θ∘C is l3.
2. Identify the Relationship:
- When the temperature of the rod changes, thermal stress affects its length. If there is no thermal stress, the length of the rod at temperature θ should equal l3 (the given length).
- Therefore, in the absence of thermal stress, we can state that:
l2=l3
3. Determine Conditions for Thermal Stress:
- If l3>l2, this indicates that the rod has expanded due to thermal stress. Thus, thermal stress is positive.
- Conversely, if l3<l2, it indicates that the rod has contracted, implying that thermal stress is negative.
4. Conclusion on Options:
- If l3=l2, there is no thermal stress, and thus the deformation does not occur.
- If l3≠l2, then thermal stress is present, and it can be either positive or negative depending on whether l3 is greater or less than l2.
5. Final Options:
- From the analysis, we can conclude:
- Option 4 is correct: l2=l3 indicates no thermal stress.
- Options 1 and 3 are also correct as they describe the conditions under which thermal stress is non-zero.
Summary of Correct Options:
- Correct options are: A, C, and D.
- We have a metallic rod with a natural length l1 at 0∘C.
- The length of the rod at a temperature θ∘C is l2.
- The given length of the rod at temperature θ∘C is l3.
- When the temperature of the rod changes, thermal stress affects its length. If there is no thermal stress, the length of the rod at temperature θ should equal l3 (the given length).
- Therefore, in the absence of thermal stress, we can state that:
l2=l3
- If l3>l2, this indicates that the rod has expanded due to thermal stress. Thus, thermal stress is positive.
- Conversely, if l3<l2, it indicates that the rod has contracted, implying that thermal stress is negative.
- If l3=l2, there is no thermal stress, and thus the deformation does not occur.
- If l3≠l2, then thermal stress is present, and it can be either positive or negative depending on whether l3 is greater or less than l2.
- From the analysis, we can conclude:
- Option 4 is correct: l2=l3 indicates no thermal stress.
- Options 1 and 3 are also correct as they describe the conditions under which thermal stress is non-zero.
- Correct options are: A, C, and D.
Similar Questions
The length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. Then natural length of the wire is
View SolutionThe length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. The natural length of the wire is
View SolutionThe length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. The natural length of the wire is
View SolutionThe length of a metal wire is l1 when the tensionin it is T1andisl2 when the tension is T2. The natural length of the wire is
View SolutionThe length of two metallic rods at temperatures θ are LA and LB and their linear coefficient of expansion are αA and αB respectively. If the difference in their lengths is to remian constant at any temperature then
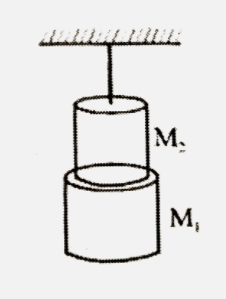
View SolutionThe length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.
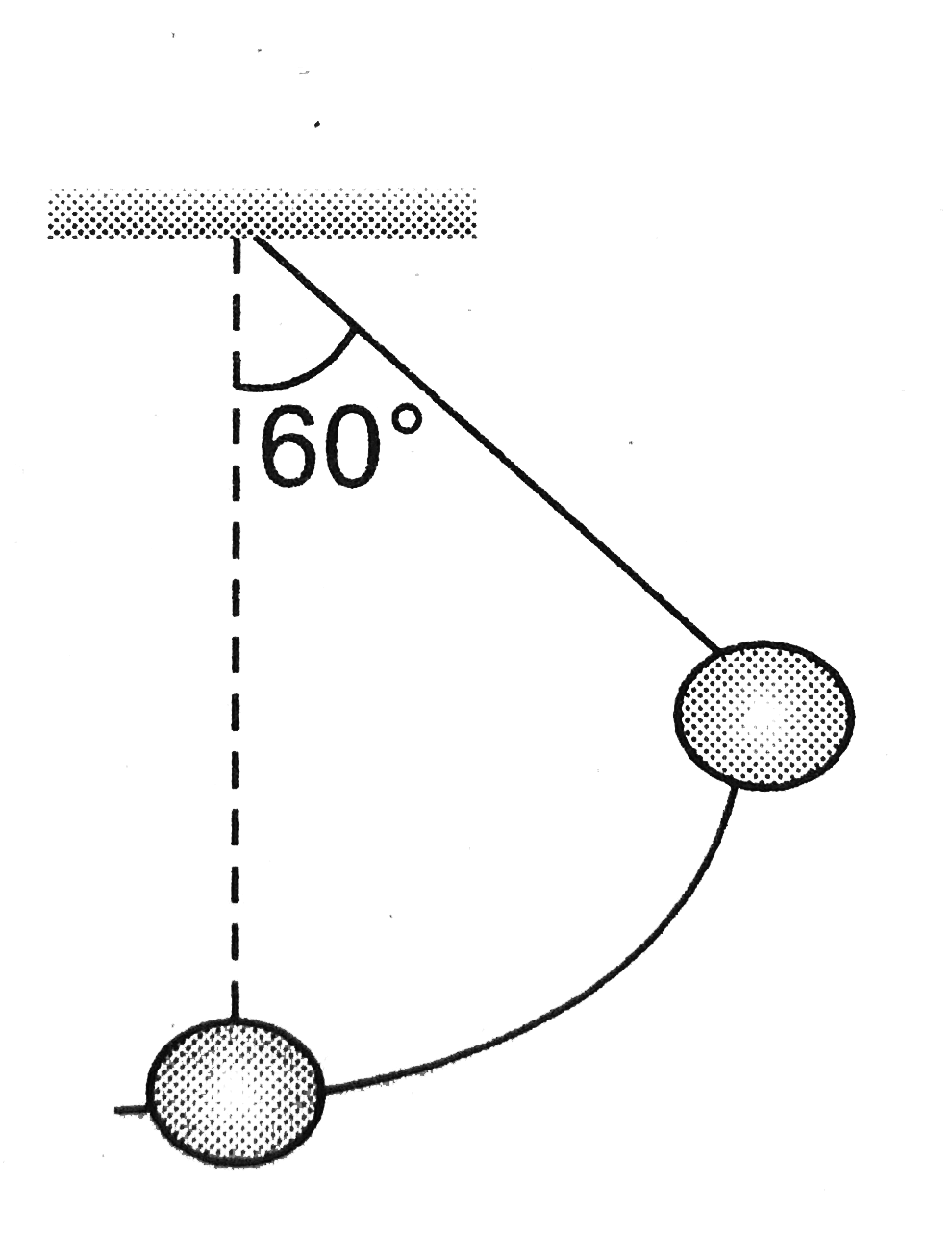
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.

View SolutionThe length of a metal wire is l1 when the tension in it is F1 and l2 when the tension becomes F2. Find the natural length of wire.
View SolutionThe co-efficient of thermal expansion of a rod is temperature dependent and is given by the formula α=aT, where a is a positive constant at T in∘C. if the length of the rod is l at temperature 0∘C, then the temperature at which the length will be 2l is
View Solution
