A sniper fires a rifle bullet into a gasoline tank making a hole below the surface of gasoline. The tank was sealed at 3.10 atm . The stored gasoline has a density of . The velocity with which gasoline begins to shoot out of the hole is
The correct Answer is:B
To find the velocity with which gasoline begins to shoot out of the hole in the tank, we can use Bernoulli's theorem. Here’s a step-by-step solution:
Step 1: Understand the scenario
We have a gasoline tank sealed at a pressure of 3.1 atm, and there is a hole 53.0 m below the surface of the gasoline. The density of gasoline is given as 660 kg/m³.
Step 2: Identify the points in the system
Let’s denote:
- Point A: the surface of the gasoline in the tank.
- Point B: the hole where the gasoline is shooting out.
Step 3: Apply Bernoulli’s equation
Bernoulli's equation states that for incompressible, non-viscous fluids, the following holds true between two points in a flow:
PA+12ρv2A+ρghA=PB+12ρv2B+ρghB
Where:
- P = pressure
- ρ = density of the fluid
- v = velocity of the fluid
- g = acceleration due to gravity (approximately 9.81 m/s²)
- h = height above a reference point
Step 4: Set up the equation
At point A (the surface):
- The pressure PA=3.1atm=3.1×105Pa
- The height hA=0 (taking the surface as the reference level)
- The velocity vA≈0 (the fluid at rest)
At point B (the hole):
- The pressure PB=Patm=1atm=1×105Pa
- The height hB=−53.0m (53 m below the surface)
- The velocity vB=v0 (the velocity we want to find)
Step 5: Substitute into Bernoulli’s equation
Substituting the known values into Bernoulli's equation gives:
3.1×105+0+0=1×105+12⋅660⋅v20−660⋅9.81⋅53
Step 6: Simplify the equation
Rearranging the equation:
3.1×105−1×105=12⋅660⋅v20−660⋅9.81⋅53
This simplifies to:
2.1×105=12⋅660⋅v20−660⋅9.81⋅53
Step 7: Calculate the gravitational term
Calculating 660⋅9.81⋅53:
660⋅9.81⋅53≈344,658
Step 8: Substitute back and solve for v20
Now substituting back:
2.1×105+344,658=12⋅660⋅v20
534658=330⋅v20
Step 9: Solve for v20
v20=534658330≈1624.6
Step 10: Take the square root to find v0
v0=√1624.6≈40.31m/s
Final Answer
The velocity with which gasoline begins to shoot out of the hole is approximately 41 m/s.
---
We have a gasoline tank sealed at a pressure of 3.1 atm, and there is a hole 53.0 m below the surface of the gasoline. The density of gasoline is given as 660 kg/m³.
Let’s denote:
- Point A: the surface of the gasoline in the tank.
- Point B: the hole where the gasoline is shooting out.
Bernoulli's equation states that for incompressible, non-viscous fluids, the following holds true between two points in a flow:
PA+12ρv2A+ρghA=PB+12ρv2B+ρghB
- P = pressure
- ρ = density of the fluid
- v = velocity of the fluid
- g = acceleration due to gravity (approximately 9.81 m/s²)
- h = height above a reference point
At point A (the surface):
- The pressure PA=3.1atm=3.1×105Pa
- The height hA=0 (taking the surface as the reference level)
- The velocity vA≈0 (the fluid at rest)
- The pressure PB=Patm=1atm=1×105Pa
- The height hB=−53.0m (53 m below the surface)
- The velocity vB=v0 (the velocity we want to find)
Substituting the known values into Bernoulli's equation gives:
3.1×105+0+0=1×105+12⋅660⋅v20−660⋅9.81⋅53
Rearranging the equation:
3.1×105−1×105=12⋅660⋅v20−660⋅9.81⋅53
2.1×105=12⋅660⋅v20−660⋅9.81⋅53
Calculating 660⋅9.81⋅53:
660⋅9.81⋅53≈344,658
Now substituting back:
2.1×105+344,658=12⋅660⋅v20
534658=330⋅v20
v20=534658330≈1624.6
v0=√1624.6≈40.31m/s
The velocity with which gasoline begins to shoot out of the hole is approximately 41 m/s.
Similar Questions
There are two holes one each along the opposite sides of a wide rectangular tank. The cross section of each hole is 0.01m2 and the vertical distance between the holes is one meter. The tank is filled with water. The net force on the tank in newton when water flows out of the holes is (density of water 1000kg/m3)
View SolutionA hollow sphere has a small hole in it. On lowering the sphere in a tank of water, it is observed that water enters into the hollow sphere at a depth of 40cm below the surface. Surface tension of water is 7×10−2N/m. The diameter of the hole is
View SolutionA hollow sphere has a small hole in it. On lowering the sphere in a tank of water, it is observed that water enters into the hollow sphere at a depth of 40 cm below the surface. Surface tension of water is 7×10−2N/m. The diameter of the hole is approximately :
View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height h0 and pressure 2p0 where rh0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown.

Find the height of the water in the long tube above the top when the water stops coming out of the hole.
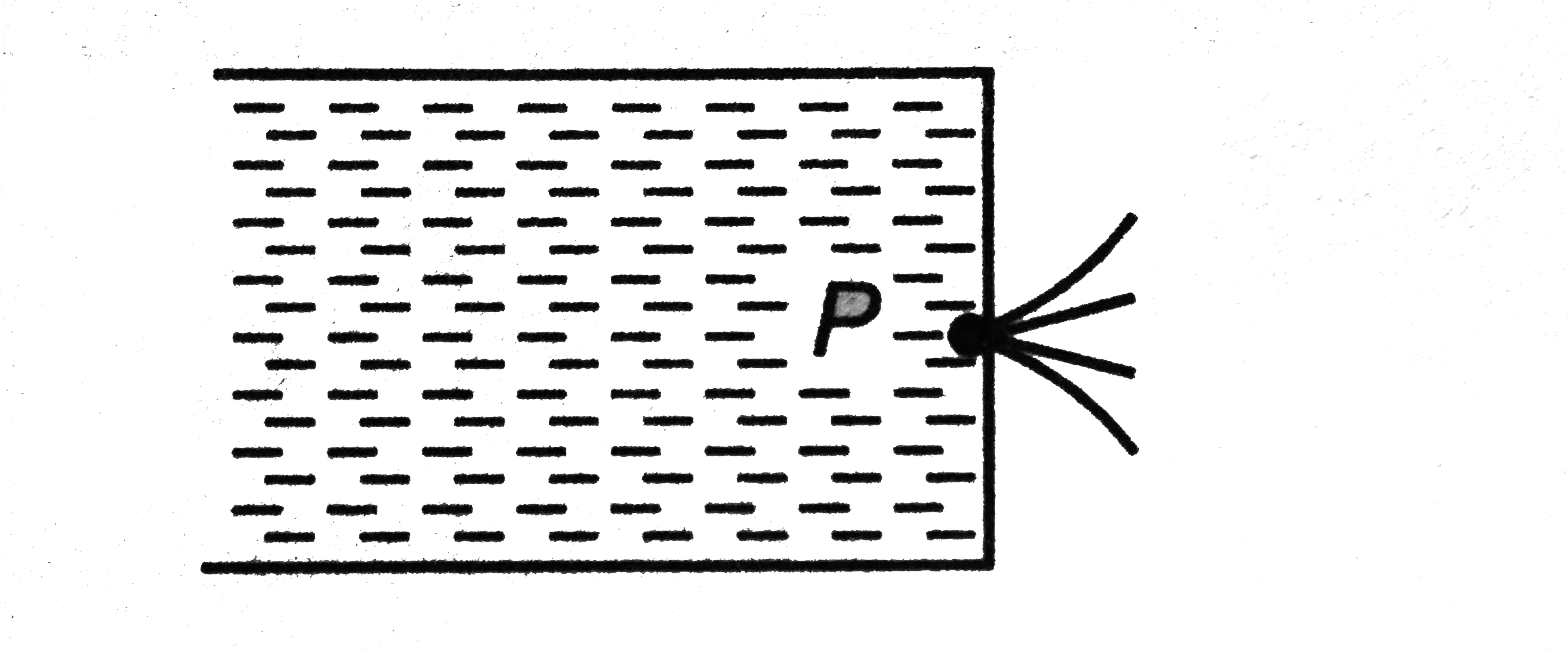
View SolutionA leakage begins in water tank at position P as shown in the figure. The gauge pressure (pressure above that of the atmosphere) at P was 5×105N/m2. If the density of water is 1000kg/m3 the initial velocity with which water gushes out is approximately
View SolutionThe range of water flowing out of a small hole made at a depth 10m below water surface in a large tank is R. Find the extra pressure (in atm) applied on the water surface so that range becomes 2R. Take 1atm=105Pa.

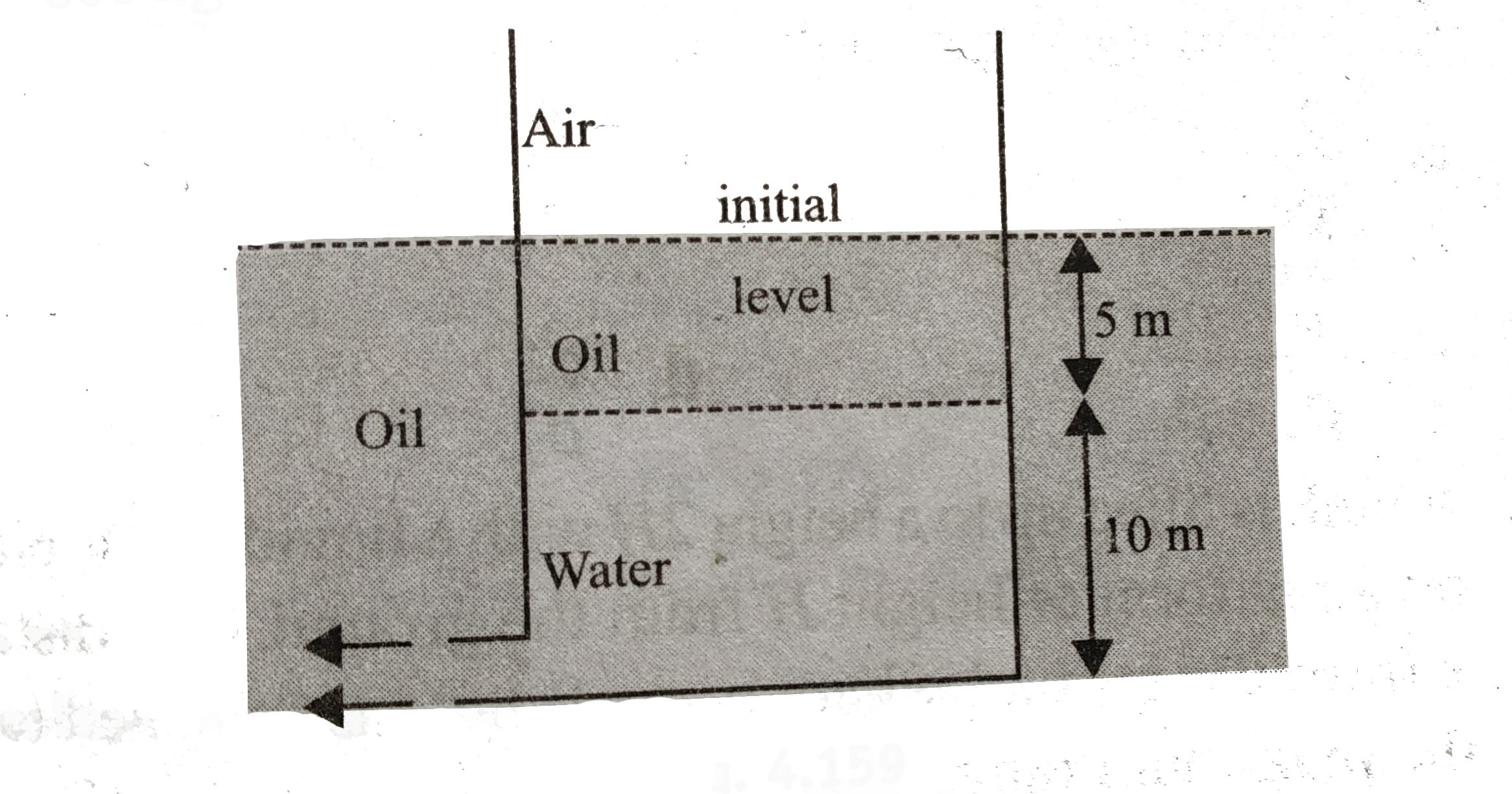
View SolutionA tank with a small orifice contains oil on top of water. It is immersed in a large tank of the same oil. Water flows through the hole. Assuming the level of oil outside the tank above orifice does not change.
a. What is the velocity of this flow initially?
b. When the flow stops, what would be the position of the oil-water interface in the tank?
c. Determine the time at which the flow stops. Density,of oil 800kg/m3.
View SolutionHeight of a tank in the form of an inverted cone is 10 m and radius of its circular base is 2 m. The tank contains water and it is leaking through a hole at its vertex at the rate of 0.02m3/s. Find the rate at which the water level changes and the rate at which the radius of water surface changes when height of water level is 5 m.
View SolutionA tank is filled by water (ρ=103kg/m3). A small hole is made in the side wall of the tank at depth 10 m below water surface. A water jet emerges horizontal from the hole and falls at horizontal distance R from it. The amount of extra pressure (in terms of atmospheric pressure) that must be applied on the water surface, so that range becomes 3R on the on the ground will be (cross section area of hole is negligible and 1 atm = 105 Pa, g = 10 m/s2)
View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height h0 and pressure 2p0 where rh0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown.

Find the speed with which water comes out of the hole
View Solution
