A tank is filled by water (ρ=103kg/m3). A small hole is made in the side wall of the tank at depth 10 m below water surface. A water jet emerges horizontal from the hole and falls at horizontal distance R from it. The amount of extra pressure (in terms of atmospheric pressure) that must be applied on the water surface, so that range becomes 3R on the on the ground will be (cross section area of hole is negligible and 1 atm = 105 Pa, g = 10 m/s2)
To solve the problem, we will follow these steps:
Step 1: Determine the initial velocity of the water jet (V1)
The velocity of the water jet emerging from the hole can be calculated using Torricelli's theorem, which states that the speed (V) of fluid flowing out of an orifice under the influence of gravity is given by:
V1=√2gh
where:
- g=10m/s2 (acceleration due to gravity)
- h=10m (depth of the hole)
Substituting the values:
V1=√2×10m/s2×10m=√200=10√2m/s
Step 2: Calculate the horizontal range (R)
The horizontal range (R) of the water jet can be calculated using the formula:
R=V1⋅t
where t is the time taken for the water to fall from the height h. The time t can be calculated using the formula for free fall:
h=12gt2⟹t=√2hg=√2×1010=√2s
Now substituting t into the range formula:
R=V1⋅t=(10√2)⋅(√2)=20m
Step 3: Determine the new velocity (V2) for range 3R
According to the problem, we want the new range to be 3R. Thus,
3R=V2⋅t
From the previous calculation, we know R=20m, so:
3R=60m
Now, we can express V2:
V2=3Rt=60√2=30√2m/s
Step 4: Apply Bernoulli's equation
Using Bernoulli's equation, we can relate the pressures and velocities at the water surface and at the hole:
P1+ρgh=P2+12ρV2
Where:
- P1 is the pressure at the water surface (atmospheric pressure + extra pressure ΔP)
- P2 is the atmospheric pressure (since the hole is open to the atmosphere)
- ρ=103kg/m3 (density of water)
Substituting the values:
P1+ρgh=P2+12ρV22
This simplifies to:
P1+(103)(10)(10)=105+12(103)(30√2)2
Calculating 12(103)(30√2)2:
=12(103)(1800)=9×105
Now substituting back:
P1+106=105+9×105
This simplifies to:
P1+106=105+9×105
Thus:
P1=105+9×105−106=8×105
Step 5: Calculate the extra pressure (ΔP)
The extra pressure ΔP is given by:
ΔP=P1−P2=8×105−105=7×105Pa
Step 6: Convert to atmospheric pressure
Since 1atm=105Pa:
ΔP=7×105105=7atm
Final Answer
The amount of extra pressure that must be applied on the water surface, so that the range becomes 3R, is:
ΔP=7atm
The velocity of the water jet emerging from the hole can be calculated using Torricelli's theorem, which states that the speed (V) of fluid flowing out of an orifice under the influence of gravity is given by:
- g=10m/s2 (acceleration due to gravity)
- h=10m (depth of the hole)
The horizontal range (R) of the water jet can be calculated using the formula:
According to the problem, we want the new range to be 3R. Thus,
Using Bernoulli's equation, we can relate the pressures and velocities at the water surface and at the hole:
- P1 is the pressure at the water surface (atmospheric pressure + extra pressure ΔP)
- P2 is the atmospheric pressure (since the hole is open to the atmosphere)
- ρ=103kg/m3 (density of water)
The extra pressure ΔP is given by:
Since 1atm=105Pa:
The amount of extra pressure that must be applied on the water surface, so that the range becomes 3R, is:
Topper's Solved these Questions
Similar Questions
A large tank is filled waith water (density =103kg/m3). A small hole is made at a depth 10 m below water surface. The range of water issuing out of the hole is R on ground. Approximately what extra pressure must be applied on the water surface so that the range becomes 2R
(take 1atm=105Pa and g=10m/s2)
 View Solution
View SolutionThe range of water flowing out of a small hole made at a depth 10m below water surface in a large tank is R. Find the extra pressure (in atm) applied on the water surface so that range becomes 2R. Take 1atm=105Pa.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A water barrel stands on a table of height h. If a small holes is punched in the side of the barrel at its base, it is found that the resultant stream of water strikes the ground at a horizontal distance R from the table. What is the depth of water in the barrel?
AR2hBR22hCR24hD4R2h
A tank if filled with water upto height H. When a hole is made at a distance h below the level of water. What will be the horizontal range of water jet ?
View SolutionA tank is filled with water upto a height H. A hole is punched in one of the walls at a depth h1 below the water surface. (a) Find the distance from the foot of the wall at which the stream strikes the floor. (6) Is it possible to make second hole at another depth so that this second stream also has the same range? If so find its depth ?
View SolutionA spherical air bubble is formed in water at a depth of 1.2 m from the surface. The diameter of the bubble is 0.6 mm and surface tension of water is 0.073Nm−1. Calculate the pressure inside . Atmospheric pressure =10.3m of water.
View SolutionA tank of height H is fully filled with water. If the water rushing from a hole made in the tank below the free surface , strikes the floor at a maximum horizontal distance , then the depth of the hole from the free surface must be
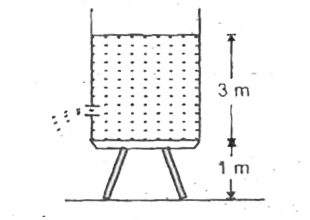
View SolutionWater is filled in a tank upto 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
 View Solution
View SolutionA tank is filled with water and two holes A and B are made in it.- For getting same range, ratio of h' and h is
 View Solution
View SolutionAt what depth below the surface of water will pressure be equal to twice the atmospheric pressure ? The atmospheric pressure is 10Ncm−2 , density of water is 103kgm−3 and g=9.8ms−2.
View Solution

