A, B, C and D are four particles with each of mass M lying on the vertices of a square of side a. They always move along a common circle with velocity v under mutual gravitational force. Find v so that they always remain on the vertices of the square
none
The correct Answer is:A
To solve the problem, we need to find the velocity v of four particles, each of mass M, positioned at the vertices of a square of side a such that they move along a common circle under mutual gravitational attraction. Here’s a step-by-step solution:
Step 1: Determine the Geometry
The particles are positioned at the vertices of a square. The diagonal of the square can be calculated using the formula:
d=a√2
This diagonal will serve as the diameter of the circle along which the particles are moving.
Step 2: Calculate the Radius of the Circle
The radius r of the circle is half the diagonal:
r=d2=a√22=a√2
Step 3: Calculate the Gravitational Forces
Each particle experiences gravitational forces due to the other three particles. We will denote the gravitational force between two masses M separated by a distance r as:
F=GM2r2
For the forces acting on one particle located at vertex A, we have:
- The distance to the particles at vertices B and D is a.
- The distance to the particle at vertex C (the opposite vertex) is √2a.
Calculating the forces:
1. Force due to particle B:
F1=GM2a2
2. Force due to particle D:
F2=GM2a2
3. Force due to particle C:
F3=GM2(√2a)2=GM22a2
Step 4: Resultant Force Calculation
The resultant force FR acting on the particle at vertex A due to particles B and D can be calculated using vector addition. Since F1 and F2 are equal and directed at right angles, we can find the resultant:
FR=√F21+F22=√2F21=√2F1=√2⋅GM2a2
Step 5: Total Force Acting on the Particle
The total force acting on the particle at A is:
Ftotal=FR+F3=√2⋅GM2a2+GM22a2
To combine these forces, we need a common denominator:
Ftotal=2√2GM2+GM2/2a2=(2√2+0.5)GM2a2
Step 6: Centripetal Force Requirement
For the particle to move in a circle, the gravitational force must provide the necessary centripetal force:
Fcentripetal=Mv2r
Setting the total gravitational force equal to the centripetal force:
(2√2+0.5)GM2a2=Mv2a√2
Step 7: Solve for Velocity v
Rearranging gives:
v2=(2√2+0.5)GM2⋅√2Ma
v2=(2√2+0.5)GM√2a
Taking the square root:
v=√(2√2+0.5)GM√2a
Final Result
Thus, the velocity v required for the particles to remain at the vertices of the square while moving along a common circle is:
v=√GM(1+2√2)2a
The particles are positioned at the vertices of a square. The diagonal of the square can be calculated using the formula:
d=a√2
This diagonal will serve as the diameter of the circle along which the particles are moving.
The radius r of the circle is half the diagonal:
r=d2=a√22=a√2
Each particle experiences gravitational forces due to the other three particles. We will denote the gravitational force between two masses M separated by a distance r as:
F=GM2r2
For the forces acting on one particle located at vertex A, we have:
- The distance to the particles at vertices B and D is a.
- The distance to the particle at vertex C (the opposite vertex) is √2a.
1. Force due to particle B:
F1=GM2a2
2. Force due to particle D:
F2=GM2a2
3. Force due to particle C:
F3=GM2(√2a)2=GM22a2
The resultant force FR acting on the particle at vertex A due to particles B and D can be calculated using vector addition. Since F1 and F2 are equal and directed at right angles, we can find the resultant:
FR=√F21+F22=√2F21=√2F1=√2⋅GM2a2
The total force acting on the particle at A is:
Ftotal=FR+F3=√2⋅GM2a2+GM22a2
To combine these forces, we need a common denominator:
Ftotal=2√2GM2+GM2/2a2=(2√2+0.5)GM2a2
For the particle to move in a circle, the gravitational force must provide the necessary centripetal force:
Fcentripetal=Mv2r
Setting the total gravitational force equal to the centripetal force:
(2√2+0.5)GM2a2=Mv2a√2
Rearranging gives:
v2=(2√2+0.5)GM2⋅√2Ma
v2=(2√2+0.5)GM√2a
Taking the square root:
v=√(2√2+0.5)GM√2a
Thus, the velocity v required for the particles to remain at the vertices of the square while moving along a common circle is:
v=√GM(1+2√2)2a
Similar Questions
Knowledge Check
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−√2Gm2l(2−1√2)B−2Gm2l(2+1√2)C−√2Gm2l(√2−1√2)D−2Gm2l(√2−1√2)
Four particles, each of mass m and charge q, are held at the vertices of a square of side 'a'. They are released at t = 0 and move under mutual repulsive forces speed of any particle when its distance from the centre of square doubles is
View SolutionFour particles each of mass m are kept at the four vertices of a square of side 'a' . Find gravitational potential energy of this system.
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
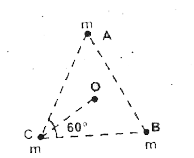
Force acting on particle C, due to particle A and B
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.

The gravitational potential at O is
View SolutionFind the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View Solution
