A particle moves in a circle with a uniform speed. When it goes from a point A to a diametrically opposite point B, the momentum of the particle changes by →PA−→PB=2 kg m/s (ˆj) and the centripetal force acting on it changes by →FA−→FB=8N(ˆi) where ˆi,ˆj are unit vectors along X and Y axes respectively. The angular velocity of the particle is
8 rad s−1
4 rad s−1
2 rad s−1
16 rad s−1
The correct Answer is:B
To solve the problem step by step, we will analyze the changes in momentum and centripetal force as the particle moves from point A to point B.
Step 1: Understand the momentum change
The momentum of a particle moving in a circle with uniform speed can be expressed as:
- At point A: →PA=m→vA
- At point B: →PB=m→vB
Given that the particle moves from point A to the diametrically opposite point B, the velocity vectors will be:
- →vA=v0^j (upward direction)
- →vB=−v0^j (downward direction)
Thus, the momentum at points A and B will be:
- →PA=mv0^j
- →PB=−mv0^j
The change in momentum is:
→PA−→PB=mv0^j−(−mv0^j)=2mv0^j
According to the problem, this change is given as 2^j kg m/s. Therefore, we can equate:
2mv0=2⇒mv0=1(Equation 1)
Step 2: Understand the centripetal force change
The centripetal force acting on the particle is given by:
- At point A: →FA=mv20r(−^i)
- At point B: →FB=mv20r^i
The change in centripetal force is:
→FA−→FB=(−mv20r^i)−(mv20r^i)=−2mv20r^i
According to the problem, this change is given as 8^i N. Therefore, we can equate:
−2mv20r=8⇒2mv20r=−8⇒2mv20=8r⇒mv20=4r(Equation 2)
Step 3: Relate the two equations
Now we have two equations:
1. mv0=1 (Equation 1)
2. mv20=4r (Equation 2)
From Equation 1, we can express m as:
m=1v0
Substituting this into Equation 2:
1v0v20=4r⇒v0=4r
Step 4: Find the angular velocity
The angular velocity ω is related to the linear speed v0 by:
ω=v0r
Substituting v0=4r:
ω=4rr=4 rad/s
Final Answer
The angular velocity of the particle is ω=4 rad/s.
---
The momentum of a particle moving in a circle with uniform speed can be expressed as:
- At point A: →PA=m→vA
- At point B: →PB=m→vB
- →vA=v0^j (upward direction)
- →vB=−v0^j (downward direction)
- →PA=mv0^j
- →PB=−mv0^j
→PA−→PB=mv0^j−(−mv0^j)=2mv0^j
According to the problem, this change is given as 2^j kg m/s. Therefore, we can equate:
2mv0=2⇒mv0=1(Equation 1)
The centripetal force acting on the particle is given by:
- At point A: →FA=mv20r(−^i)
- At point B: →FB=mv20r^i
→FA−→FB=(−mv20r^i)−(mv20r^i)=−2mv20r^i
According to the problem, this change is given as 8^i N. Therefore, we can equate:
−2mv20r=8⇒2mv20r=−8⇒2mv20=8r⇒mv20=4r(Equation 2)
Now we have two equations:
1. mv0=1 (Equation 1)
2. mv20=4r (Equation 2)
m=1v0
1v0v20=4r⇒v0=4r
The angular velocity ω is related to the linear speed v0 by:
ω=v0r
Substituting v0=4r:
ω=4rr=4 rad/s
The angular velocity of the particle is ω=4 rad/s.
Similar Questions
A particle projected from origin moves in x-y plane with a velocity →v=3ˆi+6xˆj, where ˆi and ˆj are the unit vectors along x and y axis. Find the equation of path followed by the particle :-
View SolutionThe angular momentum of a particle changes from 4kgm2s−1 to 8kgm2s−1 is 2 seconds. Calcualte the torque acting on the particle
View SolutionThe angular momentum of a particle changes from 4kgm2s−1 to 8kgm2s−1 is 2 seconds. Calcualte the torque acting on the particle
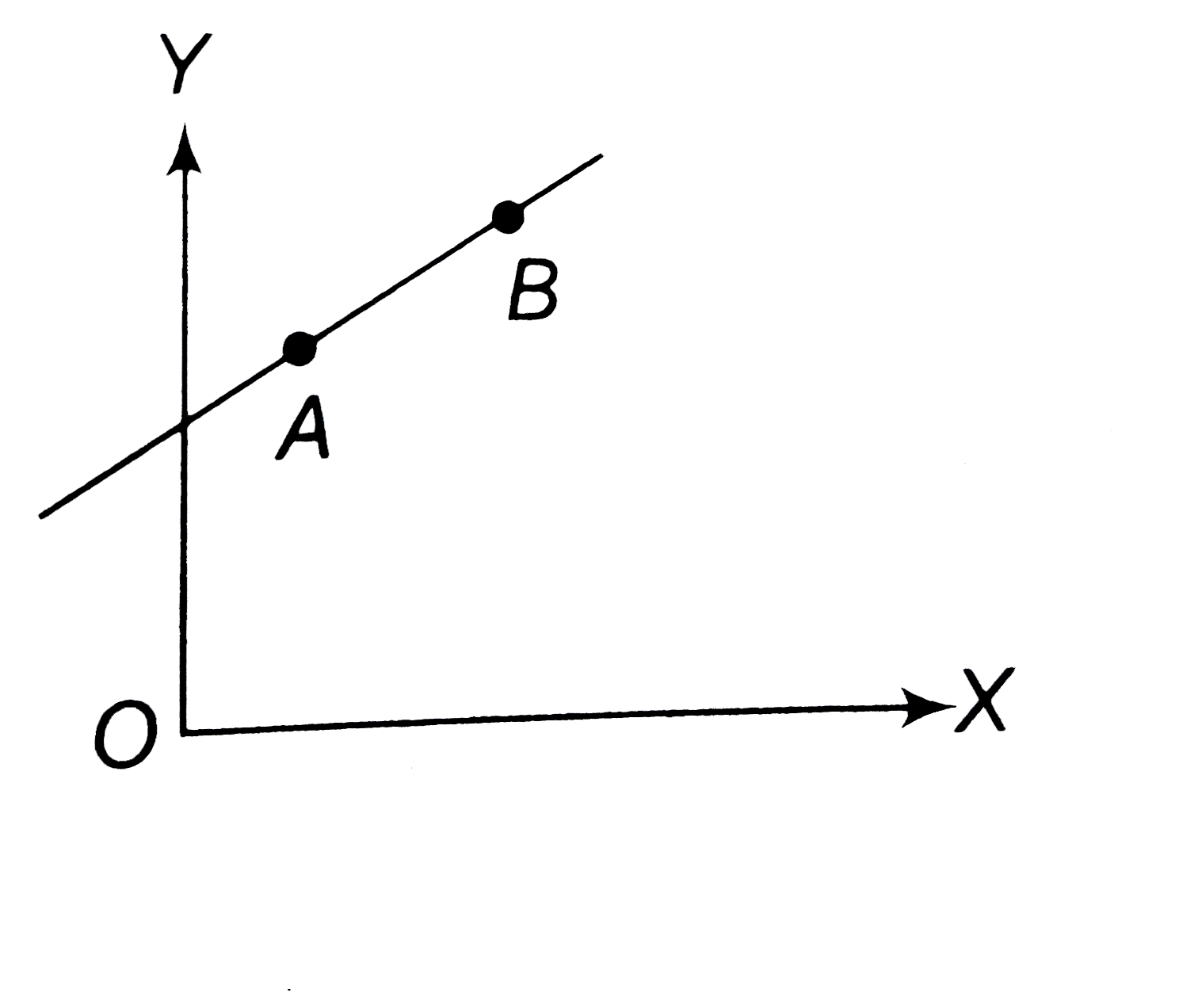
View SolutionA particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle with respect to origin O is LA when it is at A and LB when it is at B, then
View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
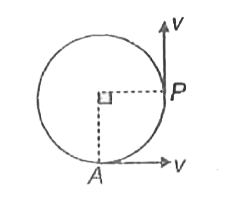
View SolutionA particle of mass 2 kg is moving in circular path with constant speed 20 m/s. The magnitude of change in velocity when particle travels from A to P will be
View SolutionA force →F=(5ˆi+3ˆj)N is applied over a particle which displaces it from its original position to the point →s=S(2ˆi−1ˆj)m. The work done on the particle is
View SolutionA particle moves 5m in the +x direction while being acted upon by a constant force→F=(4N)ˆi+(2N)ˆj−(4N)ˆk . The work done on the particle by this force is
View SolutionA particle moves from point (ˆi+ˆj)m to a point (6ˆi−2ˆj)m under the action of force (10ˆi−2ˆj)N. The work done by the force is
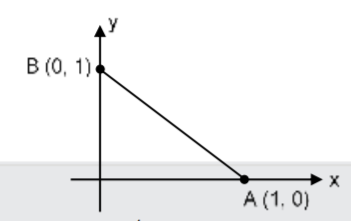
View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. evcF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.
View Solution
