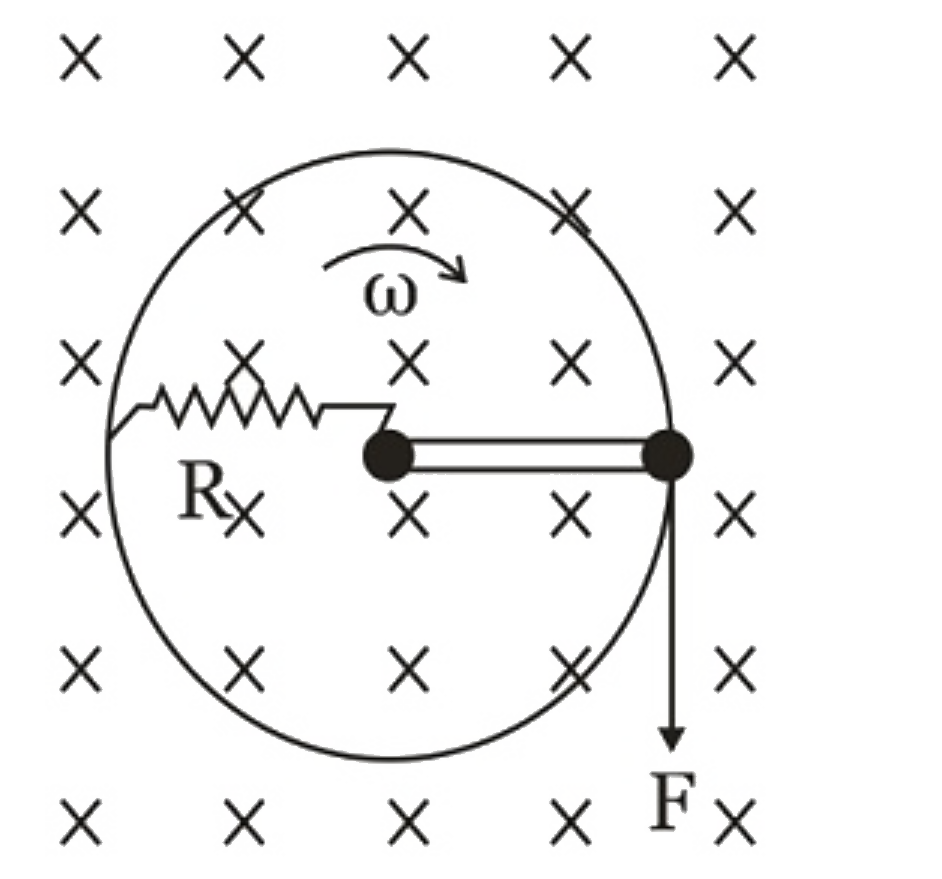
A metallic ring of mass 2 kg and radius 1 m with with a uniform metallic spoke of same mass 2 kg and length 1 m is rotated about its axis with angular velocity 1 rev sec−1. In a perpendicular uniform magnetic field B of magnitude 10 T as shown in the figure. If the central end of the spoke is connected to the rim of the wheel through a resistor R of magnitude πΩ as shown. The resistor does not rotate, It's one end is always at the centre of the ring and another end is always in contact with the ring. A force F as shown is needed to maintain the constant angular velocity of the spoke then, F is equal to (The ring and the spoke has zero resistance)
10 N
20 N
50 N
None of these
The correct Answer is:C
Step by step video & image solution for A metallic ring of mass 2 kg and radius 1 m with with a uniform metallic spoke of same mass 2 kg and length 1 m is rotated about its axis with angular velocity "1 rev sec"^(-1). In a perpendicular uniform magnetic field B of magnitude 10 T as shown in the figure. If the central end of the spoke is connected to the rim of the wheel through a resistor R of magnitude pi Omega as shown. The resistor does not rotate, It's one end is always at the centre of the ring and another end is always in contact with the ring. A force F as shown is needed to maintain the constant angular velocity of the spoke then, F is equal to (The ring and the spoke has zero resistance) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity ω in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)
 View Solution
View SolutionA metal rod of length 2 m is rotating with an angualr velocity of 100rads−1 in plane perpendicular to a uniform magnetic field of 0.3 T. The potential difference between the ends of the rod is
View Solution
Knowledge Check
- Question 1 - Select One
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ω
A copper disc of radius 1 m is rotated about its natural axis with an angular velocity 2 rad/sec in a uniform magnetic field of 5 tesla with its plane perpendicular to the field. Find the emf induced between the centre of the disc and its rim.
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/ s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
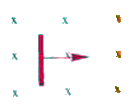 View Solution
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.View SolutionA ring of radius 0.5 m and mass 10 kg is rotating about its diameter with angular velocity of 20rads−1. Its kinetic energy is
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
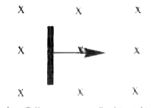 View Solution
View SolutionA metallic metre sitck moves with a velocity of 2 ms ^(-1) in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf indcued between the ends of the stick.
View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
View Solution

