A body of weight 64 N is pushed with just enough force to start it moving across a horizontal floor and the same force continues to act afterwards. If the coefficients of static and dynamic friction are 0.6 and 0.4 respectively, the acceleration of the body will be (Acceleration due to gravity = g)
The correct Answer is:2
To solve the problem, we need to calculate the acceleration of a body being pushed across a horizontal floor, given its weight, the coefficients of static and dynamic friction, and the acceleration due to gravity.
1. Identify the given values:
- Weight of the body (W) = 64 N
- Coefficient of static friction (μs) = 0.6
- Coefficient of kinetic friction (μk) = 0.4
- Acceleration due to gravity (g) = 9.8 m/s² (or can be approximated as 10 m/s² for simplicity).
2. Calculate the normal force (N):
Since the body is on a horizontal surface, the normal force (N) is equal to the weight of the body.
N=W=64N
3. Calculate the force of static friction (Fs):
The maximum static friction force can be calculated using the formula:
Fs=μs⋅N
Substituting the values:
Fs=0.6⋅64=38.4N
4. Determine the force of kinetic friction (Fk):
Once the body starts moving, the kinetic friction force acts on it. The kinetic friction can be calculated as:
Fk=μk⋅N
Substituting the values:
Fk=0.4⋅64=25.6N
5. Calculate the net force (F_net) acting on the body:
The net force acting on the body when it is moving is the applied force minus the kinetic friction force. The applied force (F) is equal to the maximum static friction force since it just started moving:
F=Fs=38.4N
Therefore, the net force is:
Fnet=F−Fk=38.4−25.6=12.8N
6. Calculate the mass (m) of the body:
Using the weight and the acceleration due to gravity, we can find the mass:
m=Wg=649.8≈6.53kg(or use g≈10 for simplicity, m≈6.4kg)
7. Calculate the acceleration (a) of the body:
Using Newton's second law, F=m⋅a, we can find the acceleration:
a=Fnetm=12.8m
Substituting m=64g:
a=12.864g=12.8g64=0.2g
Final Answer:
The acceleration of the body is:
a=0.2gm/s2
- Weight of the body (W) = 64 N
- Coefficient of static friction (μs) = 0.6
- Coefficient of kinetic friction (μk) = 0.4
- Acceleration due to gravity (g) = 9.8 m/s² (or can be approximated as 10 m/s² for simplicity).
Since the body is on a horizontal surface, the normal force (N) is equal to the weight of the body.
N=W=64N
The maximum static friction force can be calculated using the formula:
Fs=μs⋅N
Substituting the values:
Fs=0.6⋅64=38.4N
Once the body starts moving, the kinetic friction force acts on it. The kinetic friction can be calculated as:
Fk=μk⋅N
Substituting the values:
Fk=0.4⋅64=25.6N
The net force acting on the body when it is moving is the applied force minus the kinetic friction force. The applied force (F) is equal to the maximum static friction force since it just started moving:
F=Fs=38.4N
Therefore, the net force is:
Fnet=F−Fk=38.4−25.6=12.8N
Using the weight and the acceleration due to gravity, we can find the mass:
m=Wg=649.8≈6.53kg(or use g≈10 for simplicity, m≈6.4kg)
Using Newton's second law, F=m⋅a, we can find the acceleration:
a=Fnetm=12.8m
Substituting m=64g:
a=12.864g=12.8g64=0.2g
The acceleration of the body is:
a=0.2gm/s2
Similar Questions
A 60 kg body is pushed with just enough force to start it moving across a floor and the same force continues to act afterwards. The coefficient of static friction and sliding friction are 0.5 and 0.4 respectively. The acceleration of the body is
View SolutionA 60kg is pushed horizontaly with just enough force to start it moving across a floor and the same force continues to act afterwards. The coefficient of static friction and sliding friction are 0.5and 0.4 respectively the accleration of the body is
View Solution
Knowledge Check
A 20 N block is being pushed across a horizontal table by an 18 N force. If the coefficient of kinetic friction between the block and the table is 0.4, find the acceleration of the block.
A0.5m/s2B1m/s2C5m/s2D7.5m/s2A box of mass 40 kg is pusched in a straight line across a horizontal floor by an 80 N force. If the force of kinetic friction acting on the box has a magnitude of 60 N, what is the acceleration of the box?
A0.25m/s2B0.5m/s2C1.0m/s2D2.0m/s2
A body of mass 60 kg is pushed up with just enough force to start it moving on a rough surface with μs=0.5 and μk=0.4 and the force continues to act afterwards. What is the acceleration of the body ?
View SolutionA body of mass 60 kg is dragged with just enough force to start moving on a rough surface with coefficient of static and kinetic frictions 0.5 and 0.4 respectively . On applying the same force , what is the acceleration ?
View SolutionA block of mass 20kg is pushed with a horizontal force of 90N. If the coefficient of static & kinetic friction are 0.4 & 0.3, the frictional force acting on the block is: (g=10ms−2)
View SolutionA block of weight 100N lying on a horizontal surface just beging to when a horizontal to move when a horinzontal force of 25N acts on it Determine the coefficent of static friction
View Solution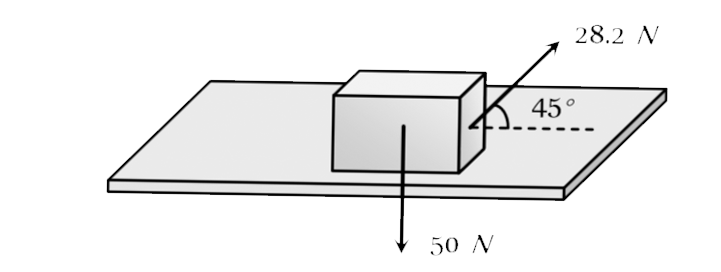
A body of weight 50 N placed on a horizontal surface is just moved by a force of 28.2 N. the frictional force and the narmal reaction are
View SolutionA slab of 40kg lying on a frictionales floor and a block of 10 kg rests on the slab as shown in the figure. The coefficients of static and kinetic friction between the slab and the block are 0.6 and 0.4 respectively. If a force of 100N is applied on the block, then the acceleration the slab will be (g=10m/s2)
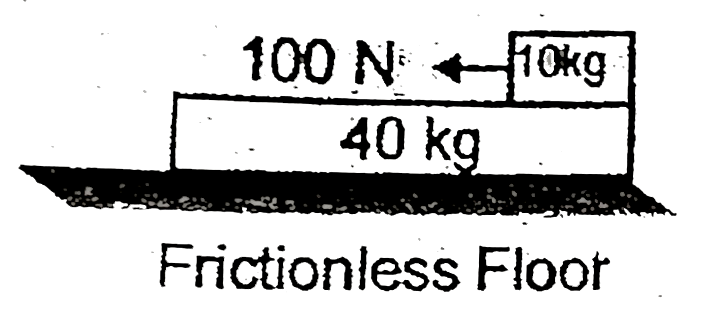
View Solution
